14. Дисперсия случайных величин. Основные свойства.
Дисперсией
С.В. Х
наз-ся мат. ожидание квадрата отклонения
С.В. Х
от её мат. ожидания. Дисперсия характеризует
степень рассеянности возможного
значения С.В. относительно её мат.
ожидания.
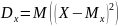
Св-ва: 1)
D(C)
= 0, C=const;
2)
D(kX)=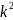
*D(x)
k=const;
3)
D(x+y)=D(x)+D(y);
X
и Y
– независим.
С.В. 4)
D(x)=M(
)
-
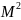(x);
Док-во:
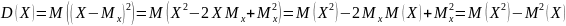
15. Тип. Законы распред-ия дискрет. C.В. Бином. Закон распред-ия.
Дискретная С.В. с
возможными значениями 0,1,2,…..n
распределена по биномиальному закону,
если вер-ти её возможных значений
опред-ся по формуле:
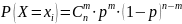
Таким образом по бином. закону распред-ся число испытаний, в кот. некот. событие А наступает в серии из n независим. испытаний.
Теорема:
Числовые характер-ки биномиально-распределённой
С.В. опред-ся по формулам: M(x)=np;
D(x)=npq;
σ(x)=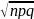
Док-во: Рассмотрим С.В. Хi – число появлений события А в i-том испытании в серии из n-независим. испытаний.
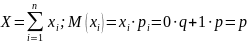
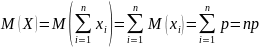
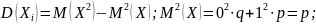
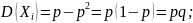
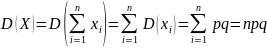
Частота события
,
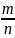распред-ся по нормированному бином.
распред-ию. Её возможные значения 0,
,
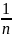1.
16. Тип. Законы распред-ия дискретных с.В. Распред-ие Пуассона.
Дискретная С.В. с
возможным значением 0,1,2……m,
распред-ся по закону Пуассона если
вер-ти наступления её возможных значений
опред-ся по формуле:
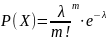, где
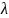=np
–
параметр распред-ия.
M(x)=D(x)=
;
σ(x)
=
.
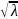Док-во:
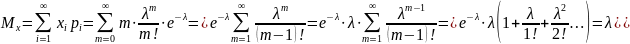
Распред-ие
Пуассона
явл. предельным случаем бином. закона
распред-ия, а именно при р
0, n
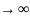. Поэтому распред-ие Пуассона наз-ся
распред-ем редких явлений. Использ-ся
в сфере массового обслуживания с простым
потоком событий, число заявок на заданный
промежуток времени – С.В. распределяемая,
по закону Пуассона.
34. Интегральная предельная теорема. Теорема Ляпунова.
Интегральная предельная теорема явл. частным случаем общей и универсальной центральной предельной теоремы. Центральная предельная теорема представляет собой группу теорем, посвящённых установлению условий, при кот. возникает норм. закон распред-ия. Среди этих теорем наиважнейшее место занимает теорема Ляпунова.
Теорема:
Если
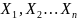– независим. С.В., у каждой из кот. сущ.
мат. ожидание
,
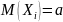дисперсия
,
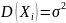абсолютный центр. момент 3-его порядка
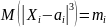и
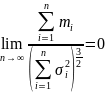
то закон распред-ия
суммы
,
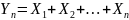при
неограниченно приближается к норм. с
мат. ожиданием
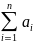и дисперсией
.
Теорему принимают без док-ва.
35. Предмет мат. Статистики. Осн. Функция мат. Статистики.
Мат. ст-ка – это раздел математики, занимающийся изучением методов сбора, систематизации и обработки стат. данных с целью выявления стат. закономерностей.
Мат. ст-ка опирается на Т.В., если Т.В. изучает закономерности случ. явлений на основе абстрактного описания исследуемого процесса, то мат. ст-ка основывается на реал. рез-тах наблюдений.
Опираясь на Т.В., мат. ст-ка занимается оценкой параметров распред-ия, а также самим распред-ем. Т.к. объем стат. данных ограничен, следовательно для получения более достоверной оценки параметров распред-ия необходимы научно-обоснованные правила.
2 осн. задачи мат. ст-ки: 1)выработка научно-обоснованных правил и рекомендаций по оценке параметров распред-ия, а также самих распред-ий. 2) проверка стат. гипотез.
Сущ. 2 способа исследования рез-тов наблюдений: сплошной и выборочный. Согласно сплошному исследованию подвергаются всевозможные рез-ты наблюдений. На практике чаще использ-ся выборочный метод, согласно кот. исследованию подвергается опред. часть, кот. принято называть выборкой.
Полученные рез-ты исследований по данным выборки распространяется на все рез-ты наблюдений с опред. Степенью доверия. В этом состоит осн. ф-ия мат. ст-ки.