9. Формула Бернулли и Пуассона.

Рассмотрим событие А, кот. может наступить с вероят-тью р в каждом из n испытаний. При чем вероят-ть наступления события А не зависит от его наступления в предыдущих испытаниях. Такие испытания принято называть независимыми.

Теорема Бернулли. Если вероят-ть наступления события А в каждом испытании постоянна, то вероят-ть того, что событие А наступит m раз в серии из n независимых испытаний равна:

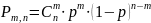, (1-p) = q ;

Док-во: n=3 m=2 В-в 3-ех независ. испытаниях событие А наступило 2 раза. А₁-событие А наст. в 1-ом испытании; А₂-во 2-ом испытании; А₃-в 3-ем испытании.

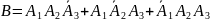
По условию

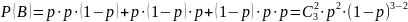
Теорема Пуассона. Если вероят-ть p наступления события А в каждом испытании постоянна и стремится к 0 при неограниченном увеличении числа испытаний . При чем 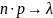, то вероят-ть того, что событие А наступит m раз в n независимых испытаниях равна: ;

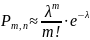Док-во: Пусть даны вер-ть наступления события А в одном испытании р и число независ. испытаний n. Обозначим 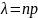. Откуда 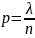. Подставим в формулу Бернулли:

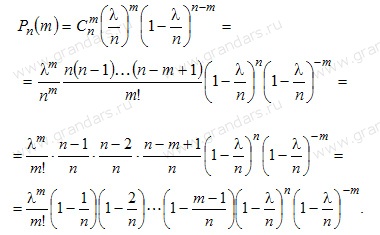
При достаточно большом n и сравнительно небольшом m, все скобки, за искл. предпослед, можно принять равным единице, т.е.

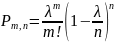Учитывая то, что n достаточно велико, правую часть можно рассмотреть при , т.е. найти предел.

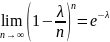. Получим

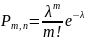
10. Локальная и интегральная теоремы Муавра-Лапласа.

Локальная теорема. Если вероят-ть р наступления события А в каждом испытании постоянна и отлично от 0 и 1, то вероят-ть того, что событие А наступит m раз в n независимых испытаниях при достаточно большом числе испытаний

, где

;

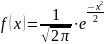
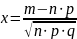Интегральная теорема. Если вероят-ть р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероят-ть того, что число m наступления события A заключено в пределах [a;b] при достаточно большом числе независимых испытаний

,

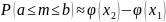где ;

; ;

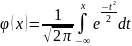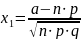Теорема Муавра-Лапласа применима для случая, когда

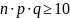
11. Способы задания закона распред-ния дискретных св. Их св-ва.

Случайной наз. величина, кот. в рез-те испытания принимает то или иное значение, заранее неизвестно какое именно.

Различают дискретные и непрерывные СВ.

СВ наз. дискретной, если она принимает изолированные друг от друга возможные значения, число кот. может быть как конечным, так и бесконечным.

Ряд распред-ния дискретной СВ – это табл., состоящая из 2-ух строк, в одной из кот. указаны возможные значения указанной величины, во 2-ой – соответствующие им вероятности.

События образуют полную группу, поэтому сумма их вероятностей будет равна 1.

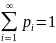
Ф-ия распределения СВ обозначается F(x). Наз. вероят-ть того, что СВ Х принимает значение находящееся левее х.

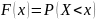
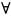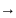Св-ва: 1) F(x) – неубывающая ф-ия, т.е. х₂ > x₁ F(x₂) > F(x₁);

2) F(-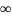 )=0; 3) F( )=1;