6Моделирование в биологии. Модели популяции, клеточные автоматы.

В биологии не всегда доступен обычный эксперимент, если в функционир-е объкта вмешивается установка то не понятна реакция объекта. «+» исп-я модели:1)На одном комплексе денных м.б. разработано несколько моделей. 2)В процессе построения м. дополнить гипотизу или упростить её.3)Можно исп-ть ЭВМ(вып-ть расчеты, рез-ты). Широко исп-ют в молек-й биологии. –Разработка структурной модели ДНК.- задача морфогенеза(проц. Упр-ющий развитием органов).

Модель однородных популяций. Общая постановка задачи:имеется популяция особей x(t)-кол-во особей в попул-ции в момент времени Проследить x(0)=N изменение кол-ва особей в популяции со временем.

1) Модель Мальтуса. (16-18вв). x(t) - кол-во особей на рассматрив площади, плотность попул на площ. k -коэф. рождаемости. В этом случае рост по exp. Модель Мальтуса. Гипотезой для построения своей модели Мальтус выбрал следующее положение: скорость изменения численности любой популяции прямо пропорциональна этой численности. Математически это положение записывается так

x'(t)=kx(t), x(0)=N.

2) Модель Ферхнюсльта-Пирла. x(t)-кол-во особей в момент набл-я, x(0)=N- в начальный момент. , где к - рождаемость, b- смертность. Разобьем время на промежутки. t_k k=0..бесконч.

(1) - по опред производной, (2) - подстановка (1) в общее уравнение с разбиен. времени. и получ (3), делаем замену hk =k hb=b и получаем конец ур-е (4). Это и есть ур-е для компа. На экране вывод в виде графика 1 пиксел = 1 ед. времени. Модель позволяет установить, при каких значениях коэффициентов рождаемости и смертности при выбранном одном и том же значении начального состояния популяции N динамика поведения популяции различна. Поведение популяции окажется полностью изучено, если будут выявлены значения коэффициентов рождаемости и смертности, при которых популяция через некоторое время от начала наблюдения выйдет на один из приведенных ниже режимов:

1) численность популяции стабилизируется на определенном уровне или незначительно колеблется около некоторого уровня (стационарный режим);

2) популяция вымирает (численность становиться равной 0). Отметим, что характер динамики популяции зависит от начальной численности N и отношения k/b.

Модель динамики двух антог-ских популяций.

Есть две популяции хишники и жертвы. x(t)-кол-во жертв, y(t) - кол-во хишников, x(0)=N y(0)=M - в нач. момент. Модель Вольтера.

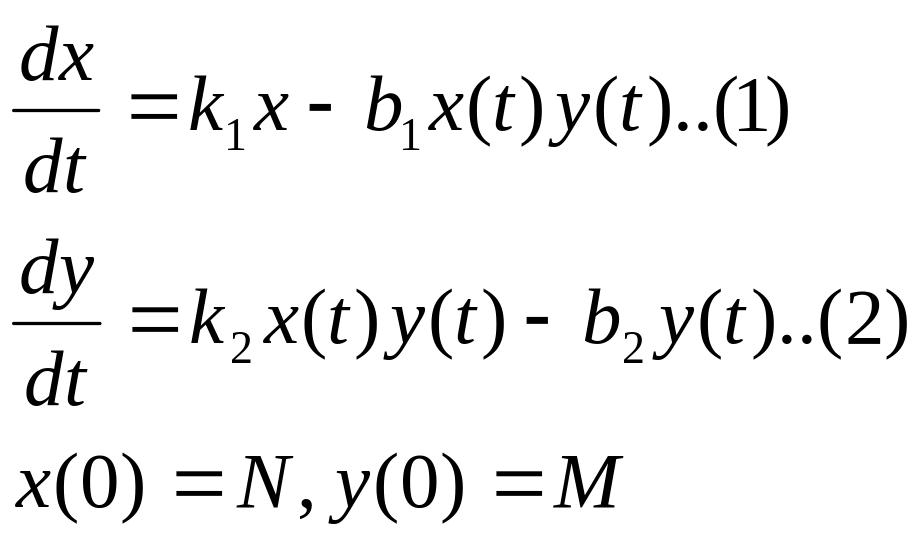
к1,к2 - коэф. рождаемости, b1,b2-коеф. смертости. Если жертвы есть, то скорость измен-я хищников = произ-ю хишников на жертв.

Заменяя во всех узловых точках первые производные на конечно-разностные отношения и рассматривая дифференциальные уравнения в математической модели поведения популяции только в узловых точках, а также разрешая получившиеся равенства относительно x_i+1, y_i+1 приходим к следующей вычислительной модели

Компьютерная модель. Работа заключается в последовательном просмотре поведения обеих популяций на графиках при различных значениях исходного количества особей N и M, а также различных значений коэффициентов рождаемости и смертности k1, k2, b1, b2. При фиксированных значениях N и M надо отыскать характерное поведение обеих популяций:1) вымирание одной и неограниченный рост другой; 2)динамическое равновесие (стационарный режим).

Замечание. 1. Надо помнить, что определяющими являются не сами значения указанных коэффициентов, а их отношения, т.е. k₁/b₁ и k₂/b₂.2. Чтобы в программе не происходило переполнения нужно выбирать коэффициенты рождаемости и смертности таким образом, чтобы b₁=O(k₂²) и k₂=O(b₂²).

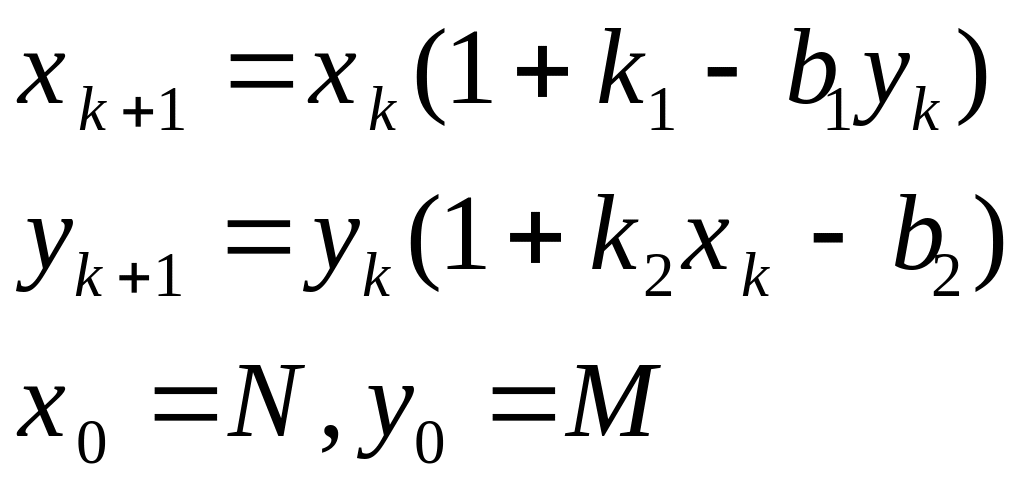
На экране выводится два графика.

Клеточные автоматы. Одномерный и двумерный случаи. Игра “Жизнь”.

Кл.Авт. - это абстракция сообщества некотор. элементарных объектов, м/у которыми возможен обмен информацией.– модель поведения клеточных сообществ(ФонНейман).–дискретн. динамич. с-ма (предст-ет собой совокупность клеток, одинаковым образом соед-х м/у собой-решетка клеточного автомата) Основными характеристиками являются: 1) дискретность в прост-ве, сущ-ют др. с др. но каждый занимает свой кант а прост-ве. 2) Развитие такого сообщ. со временем происходит скачками, дискретно. Предложил Дж.Ф. Нейман. Исследование клеточн. автоматов приводят к частичному раскрытию тайн самоорганизации в живой природе. Современ. наука синергетика. Одномерн. клеточ. авт-ты для каждой клетки рассматр. 2х соседних слева и справа(5кл.)Среди м.б. как мертвые(0) так и живые(1).Правила1) В следующий момент времени клетка б. жива если у неё жив ровно одна соседн. клетка. Двумерные клет-е авт-ты (поле неогран-но),к-я клетка м. находиться в конечном числе сост-й.Изменен. знач-я всех клеток происходит одновременно.

Рассм-им кл.авт. у которого положение клетки определяется одной коорд. Будем считать, что в момент времени клетки находились в каком-то состоянии, 1-жива, 0-мертва.

Правила получение сообщества. 1) Если клетка мертва в момент времени t она оживает в t+1 тогда и только тогда когда трое ее соседей живы в момент t. 2) Если клетка была жива в момент t, то она погибнет в момент t+1 тогда когда менее чем 2 или более чем 3 соседние клетки были живы в момент t (в первом от скуки, во втором от скученности). 3) Во всех остальных случаях состояние клетки не изменяется.

В одномерном случае берутся два соседа справа и два слева. Вычисляем сумму состояний соседей и смотрим по правилам

S=A[i-2]+ A[i-1]+ A[i]+ A[i+1]+ A[i+2]

В двумерном случае берутся соседи окружающие клетку со всех сторон (8 штук). Берём сумму и смотрим состояние по пр-лам. Вывод на экран живых в виде квадратов.

7, Моделирование в физике. Физика – это наука, в кот-й моделирование явл. важным методом исследования. Раньше физика делилась на экспер-ю и теор-ю физику, а сейчас + вычислительная физика. В физику проникли различ мат методы, но многие задачи нельзя решить с пом мат модели, следует совмещать вычислит матем-у и проведение вычислительного экспер-та, кот-й схож с лабораторным. Этапы построения модели: 1)постановка задачи; 2) Мат модель 3) Вычисл модель 4)Комп модель 5) Работа с моделью

Модель Солнце-планета. 1. Постановка задачи. В космическом пространстве находится массивное тело «Солнце». В некоторый момент времени t в поле его тяготения влетает с некоторой скоростью V тело меньшей массы m и меньших размеров - планета. Проследить судьбу этого тела( нарисовать траекторию планеты).

2.Построить мат модель движения планеты в поле тяготения Солнца.

- з-н всемирного тяготения.

- II з-н Ньютона.

,то:

х(0)=₁ , у(0)=₂ , , ,

х(0)=₁ ,

у(0)=₂ ,

3.Переход к вычислительной модели .

Выберем значение шага h

Рассмотрим систему точек t_j=jh j=1,2,3,.. .

x_j+1-2x_j+x_j-1=G(t_j)x_jh²

y_j+1-2y_j+y_j-1=G(t_j)y_jh²

j=1,2,...

4.Компьютерная модель.

DIM x,y(N)

1. Провести масштабирование.

2. Проверка 3^х типов движений.

а) по орбите.

б) за пределы.

в) упадет.

5.Работа с программой.

Шаг h=0,1

1. Построение компьютерной модели позволяет глубоко войти в сущность представлений модели.

2. Если даже компьютерная модель построена не самим обучаемым, тем не менее имея возможность воздействовать на эту модель с помощью параметров, обучаемый может глубже разобраться в сущности объекта.

Баллистическая модель. 1. Постановка: Пушка под углом к горизонту. Из нее вылетает снаряд с нач. скоростью(v₀). Сопр. Нет. Построить траекторию движения.

2. Мат модель

Модель падение тела в среде с сопротивлением. Тело находиться на высоте Н, тело отпускают, оно нач-ет падать. Ему придали нач. скорость. При относительно малых скоростях величина силы сопр-ия пропорциональна ск-ти, а при более высоких скоростях сила сопрот-я пропор-а квадрату скорости.

F_сопр=kV

Требуется выполнить моделирование тела.Нас интерисует не траектория, а тело, с какой оно скоростью падает.

1) X0=0 X^’0=0

2) рисунок

3) F=mg

ma=mg+ F_сопр

4) ma_x=mg-kv_x²

mx^’’ (t)=mg-km(x^’(t))²

5)Выбираем ∆t .Разбиваем ось времени на равностоящие промежутки. Запишем вторую и первую производные формы. Выражаем x(tk+1)

m(x(tk+1)- 2x(tk)+ x(tk+1))/ ∆t²)=mg- k((x(tk)- x(tk+1))/ ∆t²)²

x(tk+1)=(mg- k((x(tk)- x(tk-1))/ ∆t²)/m-m((x(tk-1)-2x(tk))/ ∆t²)

X(t1) =x(0)+ X^’(0) ∆t

x(t1) =0

Замечание: до каких пор мы должны проводить расчеты x(t)>=H.