
- •1.Надежность и техническая диагностика
- •2. Ремонтопригодность, сохраняемость.
- •3.Техническое состояние. Виды и события
- •4.Схема проходов состояния технического устройства
- •5.Возникновение и движение дефектов кристаличиской решетки
- •6 Развите повреждений.
- •7. Классификация дефектов.
- •8. Классификация отказов.
- •9. «Жизненный цикл» объекта.
- •Основные термины и определения эксплуатационной прочности.
- •9. Три периода жизненного цикла изделия
- •11 Конструктивные и производственные факторы
- •12 Эксплуатационные и ремонтные факторы
- •13 Признак службы техн. Контр.И надежности
- •14.Организация системы сбора и обработки данных о надежности авиационной техники
- •15. Законы распределения отказов изделий ат.(случайные велечины)
- •16. Обобщенные характеристики законов распеределения
- •19, Выбор показателей надежности
- •20.Задание требований по надежности
- •21. Показатели надежности Невосстанавливаемые изделия ат Вопрос 1. Модель функционирования
- •Вопрос 2. Количественные показатели безотказности
- •22. Показатели надежности Восстанавливаемые изделия ат
- •Вопрос 1. Модель функционирования
- •Вопрос 2. Количественные показатели долговечностинадежности восстанавливаемых изделий
- •23.Доверительные граници
- •24 Методы оценки вероятности безотказной работы гтд Вопрос 1. Метод структурных схем
- •25. Метод логических схем
- •26 Схемно-функциональный метод
- •27.Структурные модели объектов. Последовательное соединение элементов
- •Вопрос 1.Схема с последовательным соединением
- •28.Структурные модели объектов. Параллельное соединение элементов
- •Вопрос 2. Схема с параллельным соединением
- •29. Классификация методов резервирования
- •33.Виды прогназирования надежности
- •34. Прогнозирование параметров
- •Вопрос 2. Расчет упреждающих допусков
- •Вопрос 4. Модель дискретного процесса нагружения
- •Характеристики напряженного состояния
- •37.Плотность распределения вероятности отказа элементов газотурбинного двигателя
- •38. Коэффициент выработки ресурса
34. Прогнозирование параметров
Задача
прогнозирования Т.С. одномерного объекта
формулируется следующим образом: пусть
контролируемый параметр «Х» (например,
диаметр вала в подшипнике скольжения)
объекта в моменты контроля
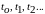 принимает значения
принимает значения
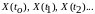 ,
по которым построен график
,
по которым построен график
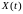 (рис.123). Необходимо по известным значениям
(рис.123). Необходимо по известным значениям
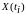 ,
где
,
где
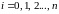 в моменты времени
в прошлом, предсказать значения
в моменты времени
в прошлом, предсказать значения
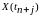 для моментов времени
для моментов времени
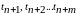 в будущем.
в будущем.
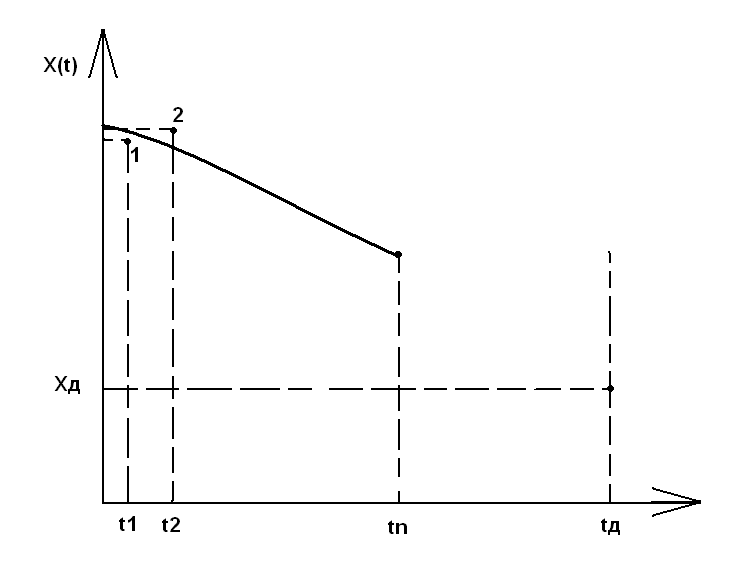
Рис.123. график изменения параметра Х по времени
Если
период между очередными моментами
контроляравен
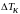 (например, 100часов), то прогнозируемый
период равен
(например, 100часов), то прогнозируемый
период равен
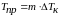 .
.
Для
прогнозирования параметров может
использоваться линейная
интерполяция – замена функции
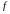 алгебраическим
двучленом
алгебраическим
двучленом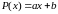 ,
однако ввиду появления больших
погрешностей ее практически не используют.
,
однако ввиду появления больших
погрешностей ее практически не используют.
При монотонной функции ее математическое представление, выраженное в виде интерполяционной формулы Лагранжа, будет иметь вид полинома порядка .
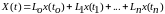 ,
,
где
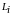 - коэффициент Лагранжа, вычисляемый
математически.
- коэффициент Лагранжа, вычисляемый
математически.
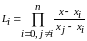 .
.
Ошибка
прогнозирования при этом не превышает
10-15%, если количество предыдущих точек
контроля
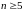 .
.
Для прогнозирования может быть использована интерполяционная формула Ньютона. Интерполяционные полиномы в форме Ньютона удобно использовать, если точка интерполировании находится вблизи начала (прямая формула Ньютона) или конца таблицы (обратная формула Ньютона).
Если узлы интерполяции равноотстоящие и упорядочены по величине, так что xi + 1 − xi = h = const, то есть xi = x0 + ih, то интерполяционный многочлен можно записать в форме Ньютона.
![]()
где
![]() ,
а выражения вида Δkyi
— конечные
разности.
,
а выражения вида Δkyi
— конечные
разности.
Вопрос 2. Расчет упреждающих допусков
Для
многих изделий АТ контролируемые
(прогнозируемые параметры имеют
нормальное распределение с математическим
ожиданием
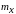 и среднеквадратическим отклонением
и среднеквадратическим отклонением
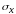 .
Эти характеристики с течением времени
часто меняются и процессы изменения
выходных параметров являются
нестационарными. При этом, в случае
неполных отказов изделий, характер
процессов изменения параметров является
монотонным. Для таких процессов возможен
расчет упреждающих
допусков,
необходимых в случае технической
эксплуатации до предотказового состояния.
.
Эти характеристики с течением времени
часто меняются и процессы изменения
выходных параметров являются
нестационарными. При этом, в случае
неполных отказов изделий, характер
процессов изменения параметров является
монотонным. Для таких процессов возможен
расчет упреждающих
допусков,
необходимых в случае технической
эксплуатации до предотказового состояния.
Значение упреждающего допуска при прочих равных условиях зависит от периодичности контроля параметров: чем больше время наработки объекта между очередными проверками, тем больше должна быть и величина упреждающего допуска.
Исходным
условием определения значения упреждающего
допуска
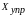 на параметр является заданная вероятность
на параметр является заданная вероятность
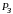 его выхода за границу рабочего допуска,
т.е. заданная допустимая вероятность
неполного отказа.
его выхода за границу рабочего допуска,
т.е. заданная допустимая вероятность
неполного отказа.
Расчет упреждающего допуска выполняется в следующей последовательности:
Определяют время наработки изделия до первого профилактического контроля из условия заданной максимальной допустимой вероятности неполного отказа.
Выбирают периодичность контроля , исходя из условия, что
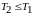 и округляют его до стандартного значения.
и округляют его до стандартного значения.По истечении периода в зоне упреждающих допусков находят параметры, которые за очередной межконтрольный период могут выйти за пределы
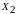 вероятностным способом.
вероятностным способом.Определяют среднеквадратическое отклонение параметра за время наработки .
При первом контроле с наработкой определяют значение контролируемого параметра, сравнивают его с допустимым отклонением и определяют упреждающий допуск при .
Выполняют контроль с наработкой , сравнивают его с допустимым отклонением и упреждающим допуском при .
Используя среднеквадратическое отклонение, выбирают упреждающий допуск для заданного параметра.
35.Модель непрерывного нагружения
Процессы,
характеризующие внешние условия,
представляются как случайная
последовательность участков, на каждом
из которых
 и
и
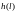 являются
стационарными случайными процессами
(стационарный процес характеризуется
независимостью среднего значения и
дисперсии от времени).Самолет в этом
случае рассматривается как линейная
динамическая система, параметры которой
рассчитываются для конструкции планера.
Процессы изменения напряжений
являются
стационарными случайными процессами
(стационарный процес характеризуется
независимостью среднего значения и
дисперсии от времени).Самолет в этом
случае рассматривается как линейная
динамическая система, параметры которой
рассчитываются для конструкции планера.
Процессы изменения напряжений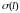 в
силовых элементах конструкции определяются
как реакции этой системы на входные
воздействия – случайные функции времени
в
силовых элементах конструкции определяются
как реакции этой системы на входные
воздействия – случайные функции времени
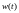 и
и
 .
.
Анализ процессов и производятся методами теории случайных процессов.
Основными
числовыми характеристиками стационарного
случайного процесса
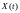 являются:
являются:
-
среднее значение – математическое
ожидание
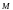 ;
;
-
центрированная случайная функция с
нулевым математическим ожиданием
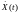 ;
;
-
корреляционная функция
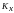 ;
;
-
спектральная плотность процесса
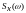 ;
;
-
дисперсия процесса
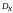 .
.
Как
показывают испытания, долговечность
изделий при случайном нагружении
существенно зависит от параметра
сложности процесса
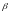 ,
определяемого как отношение средних
за единицу времени чисел экстремумов
,
определяемого как отношение средних
за единицу времени чисел экстремумов
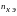 ,
и пересечений нулевого уровня
,
и пересечений нулевого уровня
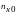 (рис.120):
(рис.120):
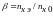 .
.
Для
процессов изменения напряжений в силовых
элементах конструкций ЛА обычно
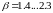 .
.
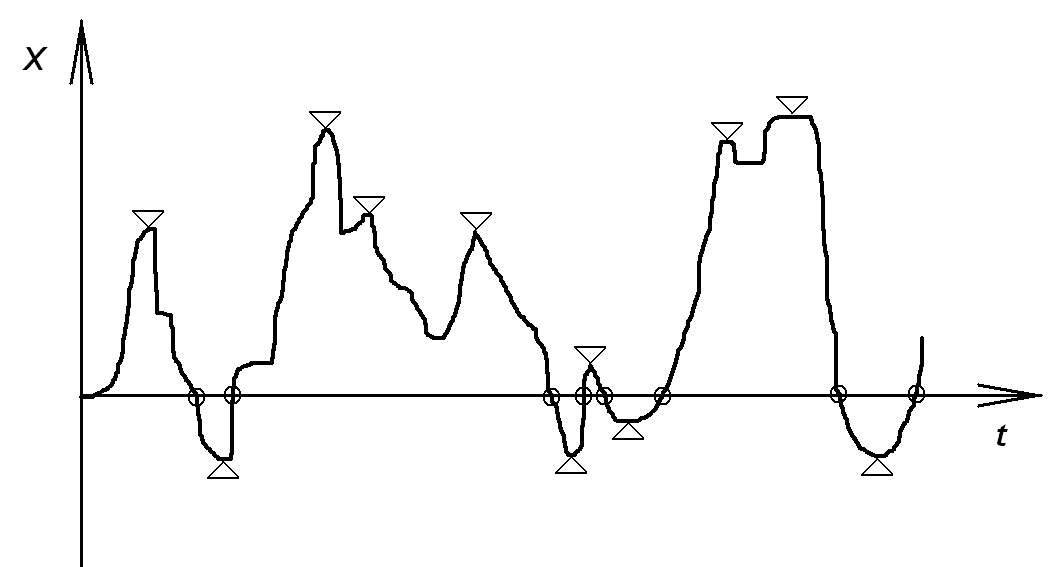
Рис.120. Стационарный случайный процесс и его характеристики:
![]() -
пересечения нулевого уровня;
-
пересечения нулевого уровня;
![]() - экстремумы
- экстремумы
Скорость
вертикального порыва ветра
 как случайная функция расстояния в
направлении движения самолета описывается
зависимостью
как случайная функция расстояния в
направлении движения самолета описывается
зависимостью
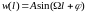 ,
,
где
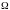 - круговая частота.
- круговая частота.
Все
характеристики должны быть получены
для всех стационарных участков типового
полета и движения самолета по ВПП. В
простейшем случае для полета принимаются
три исходных значения
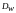 ,
соответствующие грозовой, облачной и
ясной (
,
соответствующие грозовой, облачной и
ясной (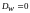 )
погоде, и указываются доли времени для
них. Для характеристики аэродрома
составляются картотеки значений
)
погоде, и указываются доли времени для
них. Для характеристики аэродрома
составляются картотеки значений
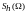 (для каждой ВПП в отдельности или
осредненные по классам). Применительно
к проектируемому самолету указывается
частота взлетов – посадок на соответствующие
ВПП.
(для каждой ВПП в отдельности или
осредненные по классам). Применительно
к проектируемому самолету указывается
частота взлетов – посадок на соответствующие
ВПП.
При
описании модели непрерывного процесса
нагружения указываются вероятностные
характеристики последовательности
стационарных участков, каждый из которых
характеризуется средним значением
напряжения
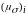 ,
спектральной плотностью
,
спектральной плотностью
 ,
продолжительностью
:
,
продолжительностью
:
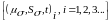 .
.
Система этих участков представляет собой блок нагружения, используемый при расчете как модель нагружения в типовом полете.
