1.2.6. Поле направлений.

Отметим, что дифференциальное уравнение в разрешенном относительно производной виде

                                                       (20)

устанавливает явную связь между координатами точки   и угловым коэффициентом касательной  к интегральной кривой в этой точке (рис. 3):

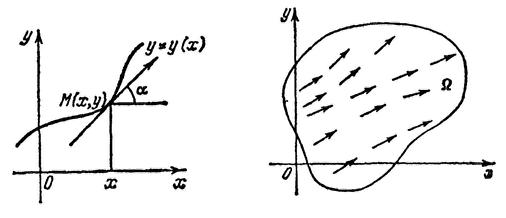
Рис. 3                                                                                  Рис. 4

.

Если функция   определена на некоторой области   плоскости, то каждой точке   соответствует некоторое направление, угловой коэффициент которого равен  . Указывая это направление единичным вектором, проходящим через точку  , мы получим на   поле направлений (рис. 4).

Интегральные кривые уравнения (20) суть кривые, для которых упомянутые направления являются направлениями касательных. Решить дифференциальное уравнение означает найти кривые, направления касательных к которым в каждой точке совпадают с направлением поля. Конечно, в данном случае интегральные кривые принадлежат области  .

Пример 4.  .

Правая часть этого уравнения определена на множестве   всех точек плоскости  , кроме точек оси  . Если точки   лежат на прямой  , то для них

,

т. е. поле направлений имеет вид, изображенный на рис. 5.

В данном случае направление прямой   совпадает с направлением поля в каждой точке этой прямой, следовательно, интегральными кривыми являются не параллельные оси  , выходящие из нулевой точки, лучи без точки (0, 0).

Для построения поля направлений, удобно рассматривать геометрические места точек, в которых касательные к интегральным кривым сохраняют постоянное направление. Такие геометрические места точек называются изоклинами.

Пример 5.  - уравнение изоклины, соответствующей определенному значению    , т. е. это окружность радиуса   (рис. 6).

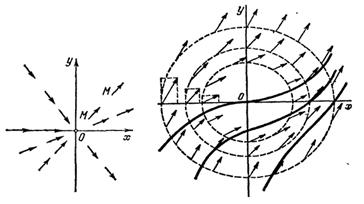
Рис. 5                                                   Рис. 6

Зная изоклины дифференциального уравнения, легко нарисовать эскиз интегральных кривых.

§ 1.3. Простейшие дифференциальные уравнения первого порядка

1.3.1. Уравнение, записанное через дифференциалы.

Пусть   и   - функции, непрерывные на некоторой области   плоскости  .

Выражение

                                 (1)

называют дифференциальным уравнением первого порядка.

На саном деле выражение (1) объединяет в себе два дифференциальных уравнения первого порядка - относительно функции   и относительно функции  .

В первом случае под решением уравнения (1) понимается функция  , определенная на некотором (зависящем от нее) интервале  , имеющая непрерывную производную и удовлетворяющая уравнению (1):

Так как дифференциал   от независимой переменной   не равен нулю, то в этом уравнении можно на   сократить и получить, что   удовлетворяет дифференциальному уравнению первого порядка, записанному в обычной форме:

.                                    (2)

Относительно решений вида   дифференциальные уравнения (1) и (2) эквивалентны.

Аналогично рассуждая, мы получим, что относительно решений вида   дифференциальное уравнение (1) эквивалентно следующему:

                                      (3)

Изучим подробнее дифференциальное уравнение (2) (относительно  ).

Пусть функция   отлична от нуля всюду на    . Тогда она в силу ее непрерывности на связном множестве   либо всюду на   положительна, либо всюду на   отрицательна. В этом случае уравнение (2) можно записать в форме разрешенной относительно  :

,                                     (2')

т. е. уравнения (2) и (2') эквивалентны на  . Если же функция   равна нулю в некоторых точках  , то уравнения (2) и (2') будут эквивалентными только на части   области  , где функция   отлична от нуля.

Пусть в точке   функция N обращается в нуль  . Если при этом  , то уравнение (2), очевидно, не имеет решения, проходящего через эту точку, - ведь второе слагаемое в левой части (2) при   равно нулю, а первое по условию не равно нулю.

 Если же наряду с равенством   выполняется также равенство  , то через точку   может проходить решение - одно или несколько или даже бесконечное число решений. Мы увидим это далее из примеров.

Подобное замечание можно сделать и в отношении дифференциального уравнения (3). Надо только в этих рассуждениях поменять местами   и  , а также   и  .

Разберем еще случай, когда обе функции   и   отличны от нуля всюду на  . В этом случае правая часть уравнения (2') тоже отлична от нуля всюду на   и имеет один и тот же знак. Но тогда решение   дифференциального уравнения (2') имеет производную   того же знака. Это показывает, что решение   строго монотонно на том интервале  , где оно задано. Но тогда оно имеет обратную непрерывно дифференцируемую функцию   на некотором интервале  . При этом

 что  показывает, что обратная функция удовлетворяет дифференциальному уравнению (3).

Итак, мы получили, что если обе функции   и   отличны от нуля всюду на  , то всякое решение уравнения (1) вида   имеет обратную функцию  , являющуюся тоже решением этого уравнения, но вида  .