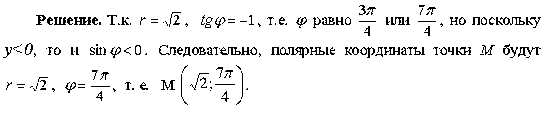28.4. Деление комплексных чисел

Деление определяется как действие, обратное умножению. Частным двух комплексных чисел z₁ и z₂≠0 называется комплексное число z, которое, будучи умноженным на z₂, дает число z₁, т. е. z₁/z₂=z, если z₂z=z_1.

Если положить z₁=x₁+iy₁; z₂=х₂+iy₂≠0, z=х+iy, то из равенства (х₂+iy₂)(x+iy)=x₁+iy₁ следует

Решая систему, найдем значения х и у:

Таким образом,

На практике частное двух комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю («избавляются от мнимости в знаменателе»).

Пример 28.2 

Выполнить деление    

Решение:

Для тригонометрической формы комплексного числа формула деления имеет вид

При делении комплексных чисел их модули, соответственно, делятся, а аргументы, соответственно, вычитаются.

28.5. Извлечение корней из комплексных чисел

Извлечение корня n-й степени определяется как действие, обратное возведению в натуральную степень.

Корнем n-й степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ωⁿ=z, т. е. , если ωⁿ= z.

Если положить z=r(cosφ+isinφ), а ω=r(cosθ+isinθ), то, по определению корня и формуле Муавра, получаем

z=ωⁿ =rⁿ(cos nθ+isin nθ)-r(cosφ+isinφ).

Отсюда имеем rⁿ=r, nθ=φ+2πk, k=0,-1,1,-2,2,... To есть

и      (арифметический корень).

Поэтому равенство принимает вид

Получим n различных значений корня. При других значениях k, в силу периодичности косинуса и синуса, получатся значения корня, совпадающие с уже найденными. Так, при k=n имеем

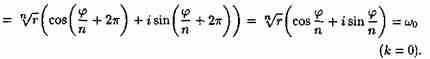
Итак, для любого z≠0 корень n-й степени из числа z имеет ровно n различных значений.

Пример 28.3

Найти значения   

Решение: а) Запишем подкоренное выражение в тригонометрической форме:

.

Стало быть,

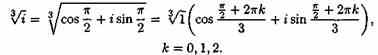
При k=0 имеем

 

при k=1 имеем

при k=2 имеем

б) Снова запишем подкоренное выражение в тригонометрической форме:

-1=cosπ+isinπ.

Поэтому

При k=0 получаем ω₀=cosp/2+isinp/2=i, а при k=1 получаем

3.1.3. Полярная система координат.

В плоскости зададим луч    (полярную ось), выходящий из точки   - полюса полярной системы координат (рис. 13, а).

Яндекс.Директ Все объявления Фейнмановские лекции Книги Ричарда Фейнмана. Закажи сейчас!ozon.ru  факультеты университетов Онлайн-справочник ВУЗов и факультетов, рейтинги и условия поступления.ucheba.ru 

Рис. 13

Положение произвольной точки   (отличной от точки  ) плоскости однозначно определяется парой чисел   -  ее полярными координатами,  где   - расстояние   до  , а   - выраженный в радианах угол между   и  . Если угол   отсчитывается против часовой стрелки от прямой  , то он считается положительным и может изменяться от 0 до  . Если угол   отсчитывается по часовой стрелке, то он считается отрицательным и может изменяться от   до 0. Точка    исключительная. Она определяется парой   , где   - произвольное число.

Пусть в плоскости, наряду с прямоугольной системой координат  ,   с началом в точке  , введена полярная система координат  ,  , так что полярная ось и положительная ось   совпадают. Тогда, полярные координаты   произвольной точки   плоскости  преобразуются в декартовы координаты   этой точки по формулам (рис. 13, б)

                              (5)

Равенства (5) называют формулами преобразования полярных координат в декартовы.

Функциональную зависимость  , заданную на некотором множестве   значений  , можно интерпретировать как множество точек   плоскости в полярной системе координат, где  ,  .

Многие кривые на плоскости могут быть описаны в полярных координатах соответствующими функциями    (многозначными или однозначными). Ясно, что в область определения функции   входят только те значения угла  , при которых  .

Построение графика функции   можно осуществить по точкам. При данном   проводим луч из точки    под углом   к полярной оси и затем на этом луче отмечаем точку   графика функции, находящуюся на расстоянии   от точки  .

Простейшей функцией в полярной системе координат является постоянная функция  . Очевидно, что ее графиком является окружность радиуса   с центром в точке  .

Другой пример   (рис. 13, в). Это спираль, раскручивающаяся из полюса  .

Функция   описывает в полярных координатах спираль Архимеда (рис. 13, г). Отметим, что здесь при  ,  . Стрелка на графике указывает направление движения точки графика при увеличении угла   .

Функция   описывает окружность радиуса единица с центром в точке   (см. рис. 13, д). Наконец, функция

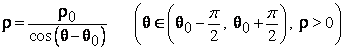
описывают такую прямую, что опущенный на нее из полюса   перпендикуляр имеет длину    и образует с полярной осью угол   (рис. 13, е).

8. Полярная система координат

Кроме прямоугольной или декартовой системы координат часто используется полярная система координат. Возьмем на плоскости направленную прямую Ох и на ней точку О (рис. 15). Положение точки М на этой плоскости определяется двумя числами: ее расстоянием r от взятой нами точки О и углом φ, образуемым отрезком ОМ с положительным направлением прямой Ох. Отсчет углов обычно ведется в направлении, противоположном движению часовой стрелки. Числа r и φ называются полярными координатами точки М, причем r называется радиус-вектором,  φ - полярным углом. Прямая Ох называется полярной осью, а точка О - полюсом полярной системы координат. Заметим, что r (как расстояние) - всегда величина положительная, а угол φ может изменяться от 0 до 2π и далее до бесконечности. Координатные линии полярной системы суть концентрические окружности с центром в точке О (r =const) и лучи, выходящие из точки О ( φ =const ). Из рис. 16 видно, что если полюс полярной системы совпадает с началом прямоугольной системы координат, а полярная ось - с осью абсцисс, то прямоугольные координаты точки М выражаются через ее полярные координаты следующим образом: Полярные координаты точки М выражаются через ее декартовы координаты такими формулами: Определяя величину φ из (52) и имея в виду, что r > 0, видим, что знак  должен быть одинаков со знаком y, а знак   - со знаком х. Отсюда по знаку sin φ и cos φ легко установить четверть, в которой лежит искомый угол. Пример 1. Декартовы координаты точки М(1, -1). Каковы полярные координаты этой точки? Пример 2. Написать уравнение прямой x = 3 в полярной системе координат. Пример 3. Построить кривую, зная, что полярные координаты ее точек удовлетворяют уравнению r = a(1 + cos φ ), (a > 0). Эта кривая называется кардиоида. Решение. Чтобы начертить эту кривую, нужно давать φ последовательно значения от φ = 0 до φ = π (с некоторым шагом) и определять по ее уравнению соответствующие значения r. Каждой из полученных пар чисел (r, φ ) соответствует в плоскости полярной системы координат единственная точка. Построив и соединив их плавной линией, получим кардиоиду (рис. 17).