Теорема Лорана
Применение рядов Лорана основано главным образом на следующей теореме Лорана:
Любая однозначная аналитическая функция в кольце представима в сходящимся рядом Лорана.
В частности, в проколотой окрестности
изолированной
особой точки
однозначная
аналитическая функция
представима
рядом Лорана, который служит основным
инструментом исследования её поведения
в окрестности изолированной особой
точки.
Тип особой точки определяется главной частью ряда Лорана в кольце с центром в этой точке:
Устранимая особая точка — главная часть ряда Лорана равна 0.
Полюс — главная часть содержит конечное число ненулевых членов.
Существенно особая точка — главная часть содержит бесконечное число ненулевых членов.
31. Изолированные особые точки
Изолированная особая точка — точка, в некоторой проколотой окрестности которой функция однозначна и аналитична, а в самой точке либо не задана, либо не дифференцируема.
Классификация
Е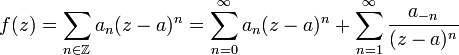
сли
—
особая точка для
,
то, будучи аналитической в некоторой
проколотой окрестности этой точки
разлагается в ряд Лорана, сходящийся в
этой окрестности.
.
Первая часть этого разложения называется правильной частью ряда Лорана, вторая - главной частью ряда Лорана.
Тип особой точки функции определяется по главной части этого разложения:
1. Изолированная особая точка
называется
устранимой особой точкой функций
если
существует конечный предел
,
где
,
и можно так доопределить функцию в этой
точке значением её предела чтобы получить
непрерывную и в этой точке функцию.
Критерии устранимости
Точка
является
устранимой особой точкой функции
тогда
и только тогда, когда ряд Лорана этой
функции не содержит отрицательных
степеней
.
Если аналитична в некоторой проколотой окрестности точки , то точка будет устранимой особенностью, если порядок роста функции в этой точке меньше единицы.
2. Изолированная особая точка z0 называется существенной особой точкой функции f(z), если предел f(z) при стремлении аргумента к z0 не существует.
Теорема о существенно особой точке
Точка z0 является существенной особой точкой функции f(z) тогда и только тогда, когда ряд Лорана этой функции содержит бесконечное число отрицательных степеней z-z0.
3. Изолированная особая точка называется полюсом , если в разложении этой функции в ряд Лорана в проколотой окрестности точки главная часть содержит конечное число отличных от нуля членов, то есть
,
где
—
правильная часть ряда Лорана.
Если
,
то
называется
полюсом порядка
.
Если
,
то полюс называется простым.
Критерии определения полюса
Точка
является
полюсом тогда, и только тогда, когда
.
Точка
является
полюсом порядка
тогда
и только тогда, когда
,
а
Точка
является
полюсом порядка
тогда
и только тогда, когда она является для
функции
нулем
порядка
32.Вычеты и их применение
П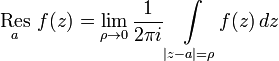
усть
—
комплекснозначная функция в области
,
регулярная в некоторой проколотой
окрестности точки
.
Вычетом функции в точке называется число
В силу регулярности функции
в
малой проколотой окрестности точки
по
теореме Коши величина интеграла не
зависит от
при
достаточно малых значениях этого
параметра, так же как и от формы пути
интегрирования. Важно только то, что
путь является замкнутой кривой в области
аналитичности функции, один раз
охватывающей рассматриваемую точку и
никаких других точек не принадлежащих
области голоморфности
.
В некоторой окрестности точки
функция
представляется
сходящимся рядом Лорана по степеням
.
Нетрудно показать, что вычет совпадает
с коэффициентом ряда
при
.
Часто это представление принимают за
определение вычета функции.
Согласно определению вычет может быть вычислен как контурный интеграл, однако в общем случае это довольно трудоёмко. Поэтому на практике пользуются, в основном, следствиями из определения:
В устранимой
особой точке
,
так же как и в точке регулярности, вычет
функции
равен
нулю. В то же время для бесконечно
удалённой точки это утверждение не
верно. Например, функция
имеет в бесконечности нуль первого
порядка, однако,
.
Причина этого в том, что форма
имеет
особенность как в нуле, так и в
бесконечности.
В полюсе
кратности
вычет
может быть вычислен по формуле:
,