13. Алгоритмы вывода окружности.
Для вывода
контура круга можно использовать
соотношение между координатами X и Y для
точек окружности
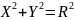и
построить алгоритм прямого вычисления
координат. Однако в этом случае необходимо
вычислять квадратный корень (как элемент
бесконечной последовательности
приближений).
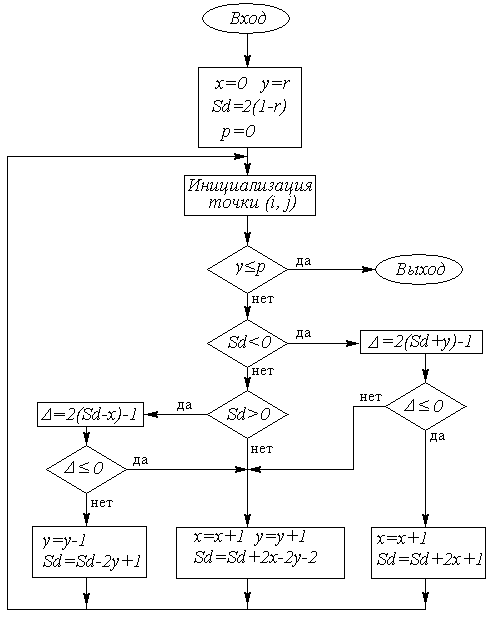
Алгоритм
изображения окружности несколько
сложнее, чем построение отрезка. Мы
рассмотрим его для случая окружности
радиуса r с центром в
начале координат. При построении
растровой развертки окружности можно
воспользоваться её симметрией относительно
координатных осей и прямых
.
Необходимо сгенерировать лишь одну
восьмую часть окружности, а остальные
её части можно получить путём отображений
симметрии. За основу можно взять часть
окружности от 0 до 45° в направлении по
часовой стрелке с исходной точкой
построения (r;
0). В этом случае координата окружности
является монотонно убывающей функцией
координаты r.
14. Алгоритмы вывода эллипса.
В каждой
точке 
эллипса
существует вектор нормали, задаваемый
градиентом функции 
.
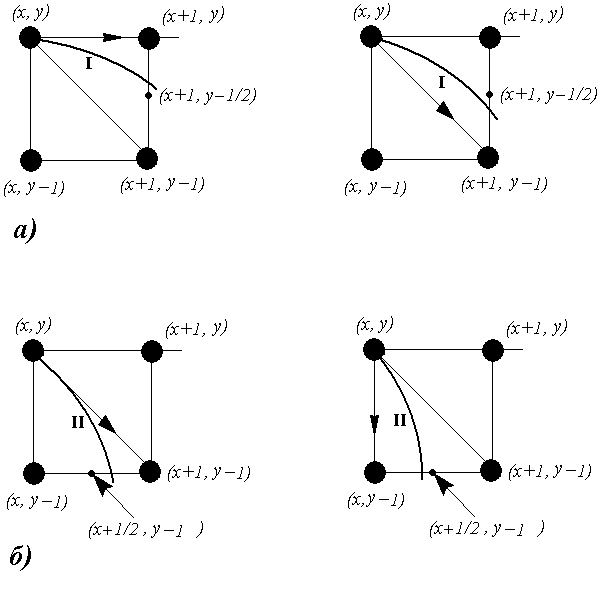
Дугу разобьем на две части: первая - с
углом между нормалью и горизонтальной
осью больше 45° (тангенс больше 1) и вторая
- с углом, меньшим 45°.
Движение
вдоль дуги будем осуществлять в
направлении по часовой стрелке, начиная
с точки 
.
Вдоль всей дуги координата является
монотонно убывающей функцией от 
,
но в первой части она убывает медленнее,
чем растет аргумент, а во второй - быстрее.
Поэтому при построении растрового
образа в первой части будем увеличивать
на
единицу и искать соответствующее
значение 
,
а во второй - сначала уменьшать
значение
на
единицу и определять соответствующее
значение
.
Направление нормали соответствует вектору
Отсюда
находим тангенс угла наклона вектора
нормали: 
.
Приравнивая его единице, получаем, что
координаты точки деления дуги на
вышеуказанные части удовлетворяют
равенству 
.
Поэтому критерием того, что мы переходим
ко второй области в целочисленных
координатах, будет соотношение 
,
или, переходя к целочисленным операциям, 
.
15. Методы улучшения растровых изображений: антиэлайзинг и дизеринг.
Устранение ступенчатости (антиэлайзинг)
При построении растрового образа линий мы сталкиваемся с эффектом ступенчатости, связанным с дискретизацией непрерывного объекта. Искажение идеального образа происходит потому, что из всего множества точек мы выбираем только те, которые оказываются ближе всего к центру элемента растра, и инициализируем этот элемент.
Для предотвращения сильных искажений в этом случае можно, во-первых, повышать разрешение растра, что позволяет отображать всё более мелкие детали объектов. Но у этого подхода есть свои чисто физические ограничения. Второй подход заключается в том, что растр рассчитывается с более высоким разрешением, а изображается с более низким - путем усреднения атрибутов пикселей первого более детального растра с определенными весами. Если веса одинаковы, то мы получаем равномерное усреднение. Лучших результатов можно достигнуть, если использовать разные веса у пикселей первого растра. На рисунке показано распределение весов при детализации пикселя экранного растра.
Распределение весов при увеличении разрешения в 16 раз
Другой метод устранения ступенчатости состоит в том, чтобы рассматривать пиксель не как точку, а как некоторую конечную область. Если рисунок черно-белый, то устранить эффект ступенчатости растра практически невозможно. Но при наличии оттенков полутонов можно задать интенсивность цвета пикселя в зависимости от площади его пересечения с областью.
Дизеринг
В компьютерной графике дизеринг используется для создания иллюзии глубины цвета для изображений с относительно небольшим количеством цветов в палитре. Отсутствующие цвета составляются из имеющихся путем их «перемешивания» (например, если необходимо получить отсутствующий в палитре фиолетовый цвет, его можно получить, разместив красные и синие пиксели в шахматном порядке).
При оптимизации изображений путем уменьшения количества цветов, применение дизеринга приводит к визуальному улучшению изображения.