20 Работа силы тяжести

С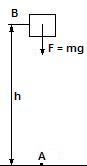 ила тяжести-сила действующая на тела вследствие его притяжения к планете

Сила тяжести, действующая на тело, является суммой сил, действующей на его отдельные части. Если считать силу тяжести однородной, то суммарная сила тяжести, действующая на тело равна произведению массы всего тела на ускорение свободного падения.

Работа силы тяжести равна изменению потенциальной энергии тела,взятому со знаком минус.

Работу силы тяжести рассмотрим на примере. Пусть тело падает под действием силы тяжести F = mg с высоты h из точки B в точку A. Формула работы силы:

A = |F||S|cosα

Подставим значения для нашего примера:

A = mgh

косинус альфа здесь равен единице.

Работа силы тяжести не зависит от траектории. То есть, если тело скатывается под действием силы тяжести с какой-то наклонной поверхности, то работа силы тяжести всё равно будет равна mgh.

На замкнутой траектории работа силы тяжести равна нулю. Значит сила тяжести является консервативной силой.

21 Консервативные силы, поле центральных сил

В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует следующее определение: консервативные силы — такие силы, работа по любой замкнутой траектории которых равна 0.Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется. Для консервативных сил выполняются следующие тождества:

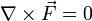•  — ротор консервативных сил равен 0;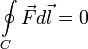

•  — работа консервативных сил по произвольному замкнутому контуру равна 0;

•  — консервативная сила является градиентом некой скалярной функции U, называемой силовой. Эта функция равна потенциальной энергии взятой с обратным знаком.

Примерами консервативных сил являются: сила тяжести, сила упругости

Модель поля центральных сил

поле, характерной особенностью которого является то, что силы, действующие на него при любом его положении в поле, всегда проходят через некоторую определенную точку называемую центром сил или центром поля. Поле центральных сил может иметь различную физическую природу, но напряженность его всегда обратно пропорциональна квадрату расстояния до центра поля.

Примерами центральных сил служат силы тяготения, направленные к центру Солнца или планеты,

кулоновские силы электростатического притяжения и отталкивания и др.  Рассмотрим важный случай поля центральных сил. Всякое силовое поле вызывается действием определенных тел. Сила, действующая на частицу А в таком поле, обусловлена взаимодействием этой частицы с данными телами. Если силы, зависят только от расстояния между взаимодействующими частицами и направлены по прямой, соединяющей эти частицы, от их называют центральными. Такими примерами служат силы гравитационные, кулоновские и упругие.

     Центральную силу, действующую на частицу А со стороны частицы В, можно представить в общем виде:

     

,

(5.8)

     где   -функция, зависящая при данном характере взаимодействия только от r - расстояния между частицами;   единичный вектор, задающий направление радиус-вектора частицы А относительно частицы В (рис.5.6).