34. Достаточные условия экстремума дифференцируемой функции.

Теорема: Первый достаточный признак экстремума функции.

Если f ’(x)>0 на интервале (x₀-б,х₀) иf ’(x)<0 на интервале (х₀,x₀+б) т.е. меняет знак с плюса на минус при переходе на точку х₀, т.е. х₀– точка максимумаf(x), а если же меняет знак с минуса на плюс, то х₀– точка минимума.

Доказательство:

Теорема:Второй достаточный признак максимума функции.

Если f(x) имеет непрерывную вторую производную в окрестности точки х0, и:

1). f ’(x₀)=0 2).f “(x₀)<0

то х₀точка максимума (аналогично, еслиf “(x₀)>0, то х₀– точка минимума)

Док-во:Возьмем окрестность, где вторая производная сохраняет знак и запишем формулу Тейлора 1-го порядка дляхиз данной окрестности.

Достаточное условие экстремума:

Непрерывная функция f(x) дифференцируема в δ-окрестности. Если при переходе черезx­₀(слева направо) производнаяf ^Iменяет знак с + на – , тоx₀–есть точкаmax, если с – на +, тоx₀– точкаmin.

Исследовать функцию на экстремум это значит:

• Найти критические точки функции y=f(x) (для этого находитсяy^Iи решается уравнениеy^I=0)

• Исследовать знак производной f ^Iслева и справа от каждой из выбранных критических точек.

В соответствии с достаточным условием экстремума выписать точки экстремума (если они есть) и вычислить значения функции в них.

35. Выпуклость и вогнутость. Критерий для функций общего вида.

Опр.Мн-во М на пл-ти назыв-ся выпуклым если вместе с любыми 2-мя точками она содержит соединяющий их отрезок.

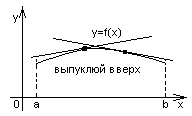
Опр. График функцииy=f(x) называется выпуклым вниз (вверх) если он расположен выше (ниже) любой касательной проведенной к графику функции на данном интервале.

λx+μy=z

λ,μ>0

λ+μ=1

Опр. Пусть ф-ция f(x) опр-на на (а,b)

Надграф-м ф-ции f(x) на (a,b) назыв-ся мн-во {(x,y):x(a,b),y≥f(x)}

Опр. Ф-ция f(x) назыв-ся выпуклой на (a,b) если её надграфик явл-ся выпуклым мн-вом.

Ф-ция f(x) назыв-ся вогнутой на (a,b) если её надграфик явл-ся вогнутым мн-вом.

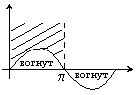
Прямая-линейная ф-ция явл-ся выпуклой и вогнутой.

Th. Для того, чтобыf(x) была выпукла наx,y(a,b)

 λ,μ≥0: λ+μ=1

f(λx+μy)λf(x)+μf(y)

I. Выпуклая

z=λx+μy

zAzB

zA=f(λx+μy)

zB=λf(x)+μf(y)

II. Выполняется нерав-во

z=λx+μy

zAzB

zAzC

zAzBzC

С принадл. надграф. F

Для вогн-ти надо, чтобы вып-сь обр-е нерав-во.

36. Выпуклость и вогнутость. Критерии для дифференцируемых и дважды дифференцируемых функций. Взаимное расположение графиков и касательных.

Th. Для того чтобы диф-аяf(x) на (a,b) была вып-й необх. и дост.x,y(a,b) вып-сь нерав-воf(y)≥f(x)+f ’(x)(y-x)

f(λx+μy)λf(x)+μf(y)

x<y

λx+μy=x+∆x

∆x=λx+μy-x=μy+x(λ-1)= μ(y-x)

λ+μ=1

f(x+∆x)-f(x) λf(x)+μf(y)-f(x)=μ[f(y)-f(x)]

∆x→0

Для x>yдоказ-ся ан-но.

λ,μ≥0: λ+μ=1

z=λx+μy

1) y:=x;x:=z

f(x)≥f(z)+f ’(z)(x-z)

2) y:=y;x:=z

f(y)≥f(z)+f ’(z)(y-z)

x-z=x-λx-μy=μ(y-x)

y-z=y-λx-μy=-λx+λy=λ(y-x)

f(y)≥f(z)+f ’(z)(x-z)

f(x)≥f(z)+f ’(z)μ(x-y) /*λ

f(y)≥f(z)+f ’(z)λ(y-x) /*μ

μf(y)+λf(x)≥μf(z)+λf(z)=f(z)=f(λx+μy)

f(λx+μy)μf(y)+λf(x)

Th. Для того чтобы дифф-я ф-ция была выпукла (вогнута) на инт. (a,b) необх. и дост., чтобы вып-сь усл-е не убыв-е (не возр-е) произв.f ’(x)↑ (f ’(x)↓)

I. Пусть ф-ция вып-а,x<y

f(y)≥f(x)+f ’(x)(y-x)

f(y)-f(x)≥f ’(x)(y-x) /:(y-x)

f(x)≥f(y)+f ’(y)(x-y)

f(x)-f(y)≥f ’(y)(x-y)

Пусть f ’(x)↑, y>x

f(y)-f(x)≥f ’(c)(y-x)≥f ’(x)(y-x)

f(y)≥f(x)+f ’(x)(y-x)

Пусть y<x

f(x)-f(y)f ’(c)(x-y)f ’(x)(x-y)

f(x)-f(y)f ’(x)(x-y)

f(y)-f(x)≥f ’(x)(y-x)

Достаточный признак выпуклости графика функции вниз.

Если функция f(x) дважды дифференц. на нтервале (a,b) и ее вторая производн.f ’’(x)>0 на интервале (a,b), то график функцииy=f(x) выпуклый вниз на интервале (a,b).

Уравнение касательной:

Возьмем X=x.Из первого вычтем второе

Поэтому y>Yследовательно график функции расположен выше касательной

Аналогично, если f ’’(x)<0 на (a,b) то график функцииy=f(x) - выпуклый вверх, на данном интервале.

Кривая y=f(x) называется выпуклой вверх (выпуклой) на интервале (a;b), если приa<x<bдуга располагается ниже касательной проведенной в любой точке (a;b).

Кривая y=f(x) называется выпуклой вниз (вогнутой) на (a;b), если приa<x<b, дуга располагается выше касательной проведенной в любой точке (a;b).