1. Критерий непрерывности функции в точке через последовательности.
Опр1.f(x) называется непрерывной в точке а, если>0>0: |f(x)-f(а)|<при |х-а|<.
Опр2. Пустьf(x)
определена в некоторой окрестности
точкиа.f(x)
называется непрерывной в точкеаесли
f(x)=f(а)
Для каждого малого изменения аргумента, сколько угодно малое изменение функции.
Если функция непрерывна во всех точках множества D, то она непрерывна на множествеD.
Любая функция непрерывна в изолированной т. множества D.
Th1.Два данных определения непрерывности равносильны.
x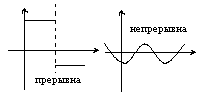
n-a,
xnD
f(xn)→f(a)
>0 >0: |x-a|<, xD=>|f(x)-f(a)|<
N n>N |xn-a|<,
|f(xn)-f(a)|<
f(xn)→f(a)
Th2. f(x) a (опр.2)
xn→a=>f(xn)→f(a)
Пусть функция f(x) не явл. непрерывной в см. 1.
0>0 не вып.>0
есть xдля кот-го |x-a|<
|f(x)-f(a)|0
=1,
xn |xn-a|<
|f(xn)-f(a)|0=>xn→a
f(xn)
f(a)
получили противоречие
2. Сумма и разность непрерывных функций.
Пусть f(x),g(x) опр. наD.
aDесли ф-ция непр-на в т., то сумма и разность также непрерывны.
xn→a
f(xn)→f(a), g(xn)→g(a)
f(xn)±g(xn)→f(a)±g(a)
Поскольку xn – произв-я, то мы получаемf±g– непр-ные в т.а
3. Произведение и частное непрерывных функций
1) Пусть f(x),g(x) опр. наD.
aDесли ф-ция непр-на в т., то произведение также непрерывно.
xn→a
f(xn)→f(a), g(xn)→g(a)
f(xn)∙g(xn)→f(a)∙g(a)
Поскольку xn – произв-я, то мы получаемf∙g– непр-ные в т.а
2) f(x),g(x) – непр.
в т.а,g(a)≠0,
то функция
непр-на
в т.а
4. Суперпозиция непрерывных функций.
Пусть f(x)-непр-на в т.а,
g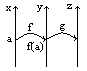
(y)-непр-на
в т.f(a)
Малому изменению а соответ-т малое изм-е f(a)
fкомпоз-яgнепр. в а
g
(f(x))-композиция
x
n→a
f(xn)→f(a)
g(f(xn))→g(f(a))
5.Непрерывность обратной функции.
Th. Функция обратная непрерывной возрастающей функции также является непрерывной.
Пусть
ф-ия y=f(x)
определена строго монотонно и непрерывна
на некотором промежутке Х и пусть У-
множество её значений. Тогда на множестве
У обратная ф-ия х=
у)
однозначно строго монотонна и непрерывна.
Равномерная непрерывность ф-ии.
Ф-ия
f(x) наз.
равномерно-непрерывной на промежутке
Х, если
>0
существует δ>0 такое что
удовлетворяющих
неравенству
<δ
выполняется неравенство
f(
.
Теорема
Кантора. Если ф-ияf(x)
непрерывна на
,
то она и равномерно непрерывна на нём.
6. Теорема об устойчивости знака непрерывной функции.
Th.Если функцияf(x) непр. в т.а иf(a)≠0, тоокрестность т.а в пределах которой функция ≠0 и сохраняет знак.
=
>0
>0:
|x-a|<
|f(x)-f(a)|<=
f(x)<f(a)+
f(a)-
<f(x)<
f(a)+
f(a)>0
f(x)>f(a)-
=
f(a)<0
f(x)<f(a)-
=
f(x)=const непр-на => (-1)∙f(x)-непр., если f-непр.
f(a)-отр. –f(x)
7. Непрерывные функции и промежуточные значения.
Опр3.Пустьf(x)-
ограниченна сверху (снизу) наX,
то естьM (m)
,xX:f(x)M
(f(x)m) . ЧислоМ (m)
называется верхней (нижней) гранью
функцииf(x)
на множествеХ. Наименьшая (наибольшая)
из верхних (нижних) граней ограниченной
сверху (снизу) наXf(x)
называется её точной верхней (точной
нижней) гранью и обозначается
f(x)
(
f(x)).
Эквивалентное определение. ЧислоM(числоm) называется точной верхней (точной нижней) гранью функцииf(x) на множествеX, если выполнены следующие два требования: 1) дляxX:f(x)M (f(x)m), 2) для > 0xX, для которого справедливо неравенство
(
)
Опр1. f(x) a
>0 >0: |x-a|<=>|f(x)-f(a)|<
Опр2. f(x) a
x
n→a=>f(xn)→f(a)
Th. О промеж-м значении.
Пусть функция f(x) непр. на отр.[a,b] и f(a)∙f(b)<0 Тогда
с[a,b]:f(c)=0
Д-во:
П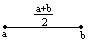
устьf(a)<0,f(b)>0
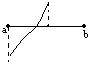
1. Если
a1:=a,
b1:=
2. Если
a1:=
,
b1:=b
a2,b2,…..
[a,b]>[a1,b1]>…
bn-an=
→0
{c}=
[ai,bi]
f(c)=0
f
(ai)<0
f(bi)>0
Пусть f(c)>0=>в нек. окр.
При дост-о большом i,f(ai)>0
f(c)=0
Следст. Пусть f(x) непр. на [a,b]
l
находится м/уf(a),f(b)
тогда с[a,b]:f(c)=l
Расс-м фун-ю g(x)=f(x)-lнепр. на отр.[a,b]
g(a)∙g(b)<0
g(c)=0 g(c)=f(c)-l=0 f(c)=l