28. Правило Лопиталя.

Если

То f(x) иφ(x) в некоторой окрестности содержат точкуx=x₀удовлетворяющую всем условиям т. Коши.

Предел отношения функций равен пределу отношения их производных.

при условии, что предел правой части равенства существует.

Правило Лопиталя применимо и в том случае когда:

• Аргумент xстремится к бесконечности

• Если отношение производных f ^Iиφⁱприxстрем. к беск. Снова приводит к неопределенности вида 0/0 или ∞/∞.

При выполнении требуемых условий правило Лопиталя можно использовать повторно.

Теорема: Если функцияf(x),g(x) дефференцирована в окресности т. а, причемf(a)=g(a)=0 и существует предел

Доказательство:

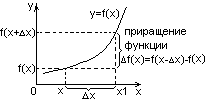
29. Формула Тейлора с остаточным членом в общей форме.

R_n+1(x)-остаточная форма формулы Тейлора

Th.p>0cмеждуxиaпри кот-м вып-ся след-е рав-во

P_n+1=(*)

Остат-й член в общем виде или член Шлемилеха-Роша

Пусть f(x) им. произв-ю в нек-й окр. т.а.

Тогда xиз этой окр-ти, для всякогоp>0 сущ-ет такая т. с м/у х и а при кот-м вып-ся (*)

Ф-ция (t) дифф-ма в окр а!

(x),(a)

(x)=0

(a)=f(x)-f(a)-

(a)=0 ф-ция непр-на, диф-ма и в этих точках=0

По т.Ролля с м/уaи х:’(c)=0

30. Формула Тейлора с остаточным членом в форме Лагранжа.

p=n+1

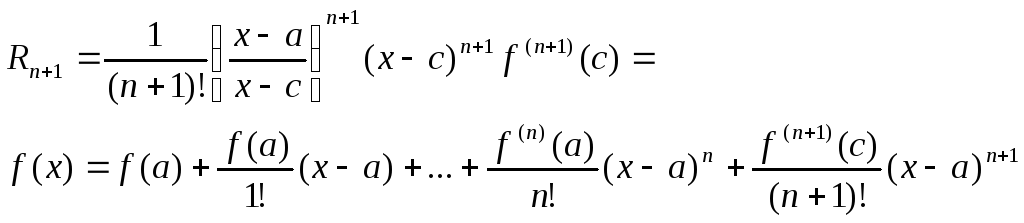
31. Разложение по формуле Тэйлора и приближенное вычисление показательной и тригонометрических функций.

1. Разложение ф-ции е^х

ряд Маклорена.

n=6,

2.

<1

k=3,

3.

32. Разложение по формуле Тэйлора и приближенное вычисление логарифмической и степенной функций.

1) Разложение ф-ции f(x)=ln(1+x)

сходится при -1<=x<=1

2) f(x)=(1+x)^

f ’(x) =α(1+x)^-1

f”(x) =α(α-1)(1+x)^-2

f⁽ⁿ⁾(x)=α(α-1)…(α-n+1)(1+x)^-n

33.Локальные экстремумы. Необходимое условие. Его недостаточность.

Опр.Пусть функцияf(x) определена всюду в некоторой окрестности точкис. Говорят, что функцияf(x) имеет в точкеслокальный максимум (минимум), если существует такая окрестность точкис, в пределах которой значениеf(с) является наибольшим (наименьшим).

Локальный максимум и минимум объединяются общим названием экстремум.

Точка x₀наз-ся точкойmax, если при любом х из некоторой δ-окрестности если выполняется неравенство:f(x) <f(x₀) приx≠x₀.

Точка x₀наз-ся точкойmin, если при любом х из некоторой δ-окрестности точкиx₀выполняется неравенство:f(x) >f(x₀) приx≠x₀.

Максимум(минимум) функции наз-ся экстремумом поскольку понятие экстремума связано с определением окрестности точки и Области Определения Функции то функция может иметь экстремум только во внутренних точках ОДЗ. Очевидно также, что функция может иметь несколько точек экстремума.

Необходимое условие экстремума:

Если функция f(x) имеет в точке х₀экстремум и дифференцируема в этой точке, тоf ^I(x₀)=0

Th.Для того чтобыf(x) –неубыв. на (a,b) необх-мо и дост-ноf ’(x)≥0 на (a,b)

Th.(Ферма). Если ф-цияf(x) опред-на в нек-й окр. т.а, диф-ма в т.а, и им. в т.а лок-йmaxилиminтоf ’(a)=0.

Опр. т.а –назыв. критич. или стац-й еслиf ’(a)=0

Теорема: Необходимый признак экстремума функции.

Е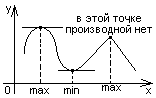сли х₀точка экстремумаf(x), то :

1). Либо не существует f’(x₀)

2). Либо f’(x₀)=0

Док-во:

1). Не сущест. f’(x₀)

2). Сущест. f ’(x₀) - по т. Фермаf ’(x₀)=0

Замечание:данные условия не являются достаточными.