18. Геометрический смысл производной. Касательная.

Рассмотрим график функции у=f(x). Проведем к графику в точке М(х,у) касательную МТ. Рассмотрим ординату этой касательной для точки х+Δх

На рисунке МN=Δх,M1N=Δy

Рассмотрим треугольник MPNtg=PN/MNPN=MN∙tgPN=tg∙Δxtg=f '(х)

Поэтому PN=f '(x)∙Δx

Н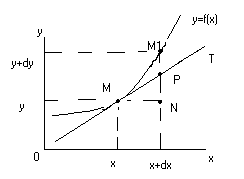о по формулеdy=f '(х)∙ΔхPN=dyДифференциал функции в точке равен приращению ординаты касательной графику функции этой функции.

Для того, чтобы f(x) имел касс-ю в т.(x,y(x)) необ-о и дост. сущ-е произв-й в т.y’(x).

y’(x)-tgугла наклона кас-й к осиOX

Сущ-е касательной означает, что сущ-ет предел сек-й.

19. Операции над дифференцируемыми функциями.

1) (u(x)+v(x))’=u’(x)+v’(x)

Δ(u(x)+v(x))=(u(x+Δx)+v(x+Δx))-(u(x)+v(x))= Δu+Δv

u’(x) v’(x)

2) (u(x)∙v(x))’=u’(x)∙v(x)+ u(x)∙v’(x)

Δ(u(x)∙v(x))=u(x+Δx)∙v(x+Δx)-u(x)∙v(x)=u(x+Δx)∙[v(x+Δx)-v(x)]+v(x)∙[u(x+Δx)-u(x)]

ΔvΔu

Делим на Δx

u(x)∙v’(x)+v(x)∙u’(x)

3)

v(x)≠0

Если |Δx|<, тоv(x+Δx)≠0

20. Дифференциал. Дифференциал суммы, произведения и частного. Инвариантность формы первого дифференциала.

Опр. Пусть функция y=f(x) имеет производную в точке х по определению производнойlim(Δy/Δx)=y'{при Δх0}

Отсюда по теореме «о связи функции, ее предела и б.м. функции»

Limf(x)=A{при хх0}f(x)+=A,0 иx0

Δy/Δx=y'+,где0 и Δх0

Δу=Δх∙у'+Δх∙(11.1.1)

Из равенства (11.1.1) видно, что произведение функции состоит из двух слагаемых, первое из которого у∙Δх – является главной частью приращения функции Δу.

Главная часть приращения функции пропорциональна приращению аргумента Δх и как говорят линейно относительно Δх.

Определение: Дифференциалом функции f(x) в точке х называется главная часть приращения функции. Дифференциалdyравен произведению производной у' на приращение аргумента, на Δх

dy=у'∙Δх (11.1.2)

Дифференциал dyназывают так же дифференциалом первого порядка.

Дифференциал независимой переменной х, т.е. дифференциал функции у=х равен dy=dx=x∙Δx=Δxdx=Δx

Поэтому формулу (11.1.2) можно записать dy=y'∙dx. Из этой формулы можно получитьdy/dx=y', т.е. обозначение производнойdy/dxможно рассматривать, как отношение дифференциалаdyкdx.

4) Итак дифференциал функции выражается одной и той же формулой, как в случае функции от независимой переменной, так и в случае функции от функции. Таким образом дифференциал функции равен произведению производной этой функции на дифференциал аргумента, где аргумент может быть и независимой переменной.

Это свойство называется Инвариантностью(неизменностью) формы дифференциала

dy=y’(x)∙dx

y’(x)=

y(x),x(t)y’(x(t))=y’(x)∙x’(t)

y(x), x(t)

dy(t)=y’(t)∙dt=y’(x)∙x’(t)∙dt=y’(x)∙dx

d(x^a)=ax^a-1dx

d(u±v)=du±dv

d(u∙v)=u∙dv+v∙du

d()=

21. Производная обратной функции. Производные обратных тригонометрических функций.

Пусть Y=f(x) – взаимообратная функцияx=(x).

Обратная теорема: Если функция Y=f(x) – строго монотонна на отрезке (а,в) и имеет в производной точкуf '(x)0, то обратная ей функцияx=(Y) имеет производную'(Y) в соответствующей точке. Причем:'(Y)=1/f '(x) илиXy'=1/Yx'

Теорема о произв. обратной функции.

Примечание: Таким образом функция равна обратной величине производной данной функции.

Правила дифференцирования обратной функции:

Yx'=1/Xy' илиdY/dX=1/(dX/dY)

1) y(x)=arcsinx

x(-1,1), y(x)(-,)

y’(x)=; x(y)=siny: [-,]→[-1,1]

x’(y)=cosy=

y’(x)=(x(-1,1))

y(x)=arccosx

x(y)=cosy [0,]→[-1,1]

x’(y)=-siny=-

y’(x)=-

(arcsinx)’=

(arccosx)’=-

arcsinx+arccosx=

2) y(x)=arctgx

x(y)=tgy (-,)→(-;+)

x’(y)=

(arctgx)’=(arcctgx)=-