37. Точки перегиба. Критерий. Касательная в точке перегиба.

Опр.Точка графика функции называетсяточкой перегибаэтого графика, если существует такая окрестность точкисоси абсцисс, в пределах которой график функции слева и справа отсимеет разные направления выпуклости.

Иногда при определении точки перегиба графика функции дополнительно требуют, чтобы этот график всюду в пределах достаточно малой окрестности точки с оси абсцисс слева и справа от с лежал по разные стороны от касательной к этому графику в точке .

Точки отделяющие выпуклую вверх часть кривой от выпуклой вниз (или наоборот) называются точками перегиба, в точках перегиба касательная пересекает кривую.

Th. Если ф-яy=f(x) во всех точках (a;b) имеет отрицательную вторую производную т.е.f ^II <0, то график ф-ии на этом интервале выпуклый вверх. Еслиf ^II >0, то он выпуклый вниз.

Достаточное условие существования точек перегиба.

Если f ^II(x) при переходе черезx₀в которой она равна 0 или не существует, меняет знак то точка графика с абсциссойx₀есть точка перегиба.

ПРИМЕР:

y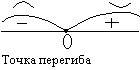=x⁵-x+5

y^I=5x ⁴-1

y^II=20x³

20x³=0

x=0

График выпуклый вверх в интервале (-;0), график вогнутый на (0; +), (0;5) – точка перегиба.

Th. (необх. усл-е сущ-е точки перегиба). Если в точке есть перегиб у дважды дифф-й ф-ции, тоf”(c)=0/

f”(c)-не полож-е, не отриц-е, значит 0

f(x)=x⁴

c=0

f”(x)=12x²

f”(c)-усл-е необх-е, но не дост-е.

(дост. усл. т. перегиба) Если ф-ция дважды дифф-ма в окр т.с, то с-точка перегиба, меняет знак.

38. Вертикальные и наклонные асимптоты графика функции.

Определение наклонной асимптоты к графику функции.

Опр.Говорят, что прямая (1)

является наклонной асимптотойграфика функциипри, если функцияf(x) представима в виде , где (2)

Опр. Говорят, что прямая x = a является вертикальной асимптотой графика функции , если хотя бы одно из предельных значений

или равно + или -.

Опр. Часть графика называется бесконечной ветвью если при движении точки по этой части, расстояние между ей и началом координат стремится к бесконечности.

Опр.Прямая называется асимптотой бесконечной ветви графика функции, если при удалении точки от начала координат по этой ветви, расстояние до данной прямой стремится к нулю.

Теорема 1:x=a(вертикальная прямая) – является асимптотой для бесконечно вертикальной ветви графика функцииy=f(x), тогда когдаf(x), приxa.

Теорема 2:Критерий существования наклонной асимптоты прямаяy=kx+bявляется асимптотой для правой (левой) ветви графика функции тогда, когда существует предел при :

Док-во:ТочкаM0(x₀,y₀) и прямая

L:Ax+By+Cz=0, то расстояние

Пустьy=kx+b

асимптота =>

d(M,l)0=>

kx-f(x)+b0

тогда f(x)-kxb

при x+

существует предел:

Теорема: Необходимый признак существования наклонной асимптоты.Если прямаяl:y=kx+b

наклонная асимп. для правой наклонной ветви, то:

Док-во:

Пример:

x=1 – верт. Асимптота, т.к.

f(x), когдаx1

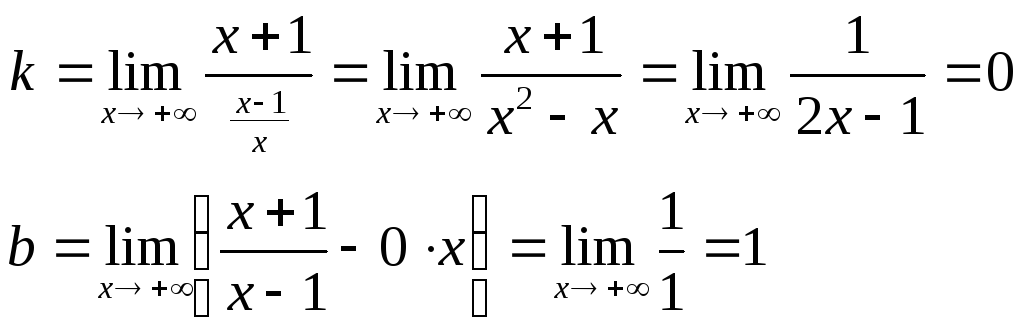
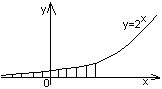
Вывод:y=0y+1 – наклонная асимптота для левой и правой ветви.

Для отыскания вертикальной асимптоты нужно найти х вблизи которого функция f(x) возрастает по модулю. Обычно это точки разрыва второго рода.

Если хотя бы один из этих пределов не существует, то кривая асимптоты не имеет. Если k=0,bимеет конечное значение, то асимптота наз-ся горизонтальной.