
- •1.1.1 Физические модели: Материальная точка, система материальных точек, абсолютно твердое тело, сплошная среда. Пространство и время. Кинематическое описание движения. Относительность движения.
- •2.6.2 Ток смещения. Система уравнений Максвелла в интегральной и диффириенциальных формах
- •1.1.2 Скорость и ускорение при криволинейном движении. Нормальное и касательное ускорения. Прямолинейное движение точки.
- •1.1.3 Движение точки по окружности. Угловая скорость и угловое ускорение. Вектор угловой скорости.
- •1.1.4 Смысл интеграла и производной в приложении к физическим задачам.
- •1.2.1 Основная задача динамики. Понятие состояния в классической механике. Границы применимости классического способа описания движения частиц.
- •I.2.2 Первый закон Ньютона и понятие инерциальной системы отсчёта.
- •I.2.3 Масса и сила. Эталон массы в си. Уравнения движения. Второй закон Ньютона как уравнение движения. Сила как производная импульса.
- •1.2.4 Третий закон Ньютона и закон сохранения импульса.
- •1.2.5 Неинерциальные системы отсчёта. Сила инерции. Принцип Даламбера.
- •2.6.1. Фарадеевская и Максвелловская трактовки явления электромагнитной индукции.
- •1.2.6 Аддиативность массы. Центр масс (инерции). Теорема о движении центра инерции. Система центра инерции.
- •2.5.2 Пара, диа и ферромагнетики и их природа.
- •I.2.7 Момент силы и момент импульса. Уравнение движения и равновесия твёрдого тела (уравнение моментов).
- •2.7.3 Движение проводника в магнитном поле. Генератор переменного тока.
- •2.5.3 Теорема о циркуляции вектора магнитной индукции в магнетике. Основные уравнения магнитостатики магнетиков.
- •2.4.4 Закон полного тока. Основные уравнения магнитостатики в вакууме.
- •I.2.8 Момент инерции тела относительно оси. Теорема Штейнера. Основной закон динамики вращательного движения.
- •2.4.5. Рамка с током в однородном магнитном поле. Момент сил, действующих на рамку. Магнитный момент. Потенциальная энергия витка с током во внешнем магнитном поле.
- •1.3.6. Консервативные и неконсервативные силы. Потенциальная энергия.
- •1.3.7 Закон изменения механической энергии. Закон сохранения энергии.
- •1.4.1 Инерциальные системы отсчёта и принцип относительности Галилея. Инварианты преобразований Галилея.
- •2.5.1 Молекулярные токи. Гипотеза Ампера. Намагниченность (вектор намагниченности). Неоднородная намагниченность. Длинный соленоид с магнетиком.
- •2.3.4. Сторонние силы. Эдс источника тока.
- •2.4.8 Магнитная энергия тока. Плотность магнитной энергии.
- •1.4.2 Постулаты специальной теории относительности. Преобразования Лапласа.
- •5.2. Общие св-ва жидкостей и газов
- •1.4.3 Относительность длин и промежутков времени. Абсолютные и относительные скорости и ускорения.
- •2.4.6 Закон взаимосвязи массы и энергии. Инварианты преобразования. Преобразования импульса и энергии.
- •1.4.4 Релятивистская динамика. Уравнения движения релятивистской частицы. Инвариантность движения относительно преобразованя Лоренца.
- •2.3.7 Движение проводника в магнитном поле. Генератор переменного тока.
- •1.4.6. Закон взаимосвязи массы и энергии. Инвариантные преобразования.
- •1.5.1. Кинетическое описание движения жидкости.
- •2.4.7 Явление электромагнитной индукции. Правило Ленца. Флюксметр. Явление самоиндукции.
- •I.5.5 Стационарное движение идеальной жидкости. Уравнение Бернулли.
- •I.5.6 Гидродинамика вязкой жидкости. Коэффициент вязкости.
- •I.5.7 Течение по трубе. Формула Пуазейля.
- •1.5.9 Упругие натяжения. Закон Гука. Растяжение и сжатие стержней.
- •2.1.1 Предмет классической электродинамики. Идея близкодействия. Поле. Электрический заряд и напряжённость электрического поля. Дискретность заряда.
- •2.1.2 Закон кулона. Принцип суперпозиции. Электрический диполь.
- •2.4.2 Закон Био-Савара-Лапласа. Магнитное поле простейших систем. Взаимодействие токов. Определение единицы силы тока – ампера.
- •2.1.3 Силовые линии, их густота. Поток вектора. Электростатическая теорема Остроградского-Гаусса и её применение.
- •2.1.4 Работа электростатического поля. Циркуляция вектора напряжённости электростатического поля.
- •2.3.6 Правила Кирхгоффа.
- •2.1.5 Потенциал. Связь потенциала с напряжённостью электрического поля. Энергия взаимодействия электрических зарядов. Энергия диполя во внешнем электростатическом поле.
- •2.2.1 Диэлектрики и их поляризация. Полярные и неполярные диэлектрики. Поляризованность (вектор поляризации). Неоднородная поляризованность. Сегнетоэлектрики.
- •2.2.2 Электрическое поле в диэлектрике. Вектор электрического смещения (электрической индукции). Теорема Остроградского-Гаусса для диэлектрика. Основные уравнения электростатики дилектриков.
- •2.2.3 Граничные условия на границе раздела «диэлектрик-диэлектрик»
- •2.4.3 Движение заряженной частицы в электрическом и магнитном полях. Эффект Холла.
- •2.2.4 Проводник в электростатическом поле. Граничные условия на границе «проводник - вакуум» и «проводник - диэлектрик». Электростатическая защита.
- •2.3.2 Законы Ома и Джоуля-Ленца в интегральной и дифференциальных формах.
- •2.3.3 Сторонние силы. Эдс источника тока.
- •2.4.1 Сила Ампера. Вектор магнитной индукции. Принцип суперпозиции. Сила Лоренца.
- •2.3.5 Работа и мощность электрического тока, кпд
- •1.3.1 Закон сохранения импульса. Реактивное движение. Абсолютно неупругий удар.
- •1.3.2 Закон сохранения момента импульса.
- •1.3.3 Движение в центральном поле. Законы Кеплера. Закон всемирного тяготения. Масса инерционная и гравитационная.
- •1.3.4 Работа и кинетическая энергия. Мощность.
- •1.3.5 Энергия вращательного движения.
2.4.7 Явление электромагнитной индукции. Правило Ленца. Флюксметр. Явление самоиндукции.
В замкнутом проводящ контуре, при измен потока маг индукции обхватываемого этим контуром возникает Эл ток наз током индукции. Значен индук тока назависит от способа изменения потока маг индукции, а определяется скоростью его изменения. Возникающий в цепи индукт ток описывается
знач
ЭДС Эл-маг индук. и подчин зак Фарадея:
какова не была причина изменен потока
Эл-маг индук, охватываемого замкнут
провод-м контуром в контуре возник ЭДС
описыв-мая по завис
![]() [B].
Знак минус показ что поле индук тока
направлено навстречу потоку и опред-ся
по правилу Лоренца т.е. индук ток в
контуре имеет всегда такое направ что
создаваем им маг поле препятсвует измен
маг потока вызываем этот ток точк зрения
Максвелла: всякое переменное магнитное
поле вызыв в округл прост-ве возник-ние
Эл поля вследствии чего ЭДС самоундук
может быть представ как циркул вектора
напряж-ти от маг потока
[B].
Знак минус показ что поле индук тока
направлено навстречу потоку и опред-ся
по правилу Лоренца т.е. индук ток в
контуре имеет всегда такое направ что
создаваем им маг поле препятсвует измен
маг потока вызываем этот ток точк зрения
Максвелла: всякое переменное магнитное
поле вызыв в округл прост-ве возник-ние
Эл поля вследствии чего ЭДС самоундук
может быть представ как циркул вектора
напряж-ти от маг потока
![]() Если
в однород маг поле вращать рамку то в
ней будет возникать ЭДС подчиняющ
гармонич закону Ei=Emaxsint
ω
t
ω-
угол поворота рамки
Если
в однород маг поле вращать рамку то в
ней будет возникать ЭДС подчиняющ
гармонич закону Ei=Emaxsint
ω
t
ω-
угол поворота рамки
Если в однород поле поместить массив проводник то в нем возник индук ток (ток Фуко)Эл ток текущ в замкнут контуре создает вокруг себя маг поле которое согласно зак Био-Савара-Лапласа пропорционал знач индукт тока Ф=LJ где L- коэф пропор-сти – индуктив контура явс возникнов ЭДС индукции в проводящ контуре при изменен в нем силы тока наз самоиндукц [L]=Гн Индук соленоида определ по зависим-ти L=μμoN2S/L μ-маг прониц сердец N – Кл-во витков S- площадь витка L-длина образующей соленоида
согласно зак Фарадея ЭДС самоиндук сожно записать в виде
![]() т.к.
индуктив контура явл велич пост
то ЭДС самоиндук приводится к выражению
т.к.
индуктив контура явл велич пост
то ЭДС самоиндук приводится к выражению
Ei=-L*dI/dt “-” обусловлен правилом Ленца. Таким образом контур, обладая определен индуктив-ю преобрет некоторую эл инертность, заключ в том что любое изменен тока тормозится тем сильнее чем бюльше индуктив контура. Явлен возникнов-я ЭДС в одном из контуров при изменен силы тока в другом наз взаимной индук.
I.5.5 Стационарное движение идеальной жидкости. Уравнение Бернулли.
![]()
Для
жидкости удобно вести скалярное поле
скоростей и провести линии, касательные
к которым в каждой точке является вектор
скорости, такие линии наз-ся линиями
тока. Совокупность линий тока образуют
трубку тока. Рассечем трубку тока
перпендикулярной площадкой.
![]()
Число линий тока, пересекающих площадку назовем потоком вектора скорости.
![]() -
поток для любого векторного поля. Если
выбрать замкнутую поверхность,
-
поток для любого векторного поля. Если
выбрать замкнутую поверхность,
![]()
Если течение жидкости стационарно, т.е. жидкость не теряется в трубке тока, то число линий тока, входящих в поверхность = числу выходящих из поверхностей линий тока.
Уравнение неразрывности струи -
υ1S1=υ2S2
=> υS=const.
Применим теорему Остроградского, поток
вектора -
![]()
![]() ;
Fcosα=pS => p=Fcosα/S=Fп/S
;
Fcosα=pS => p=Fcosα/S=Fп/S
Давление – величина, численно равная
нормальной силе, действующей на единицу площади.
Для жидкостей можно записать закон сохранения энергии.
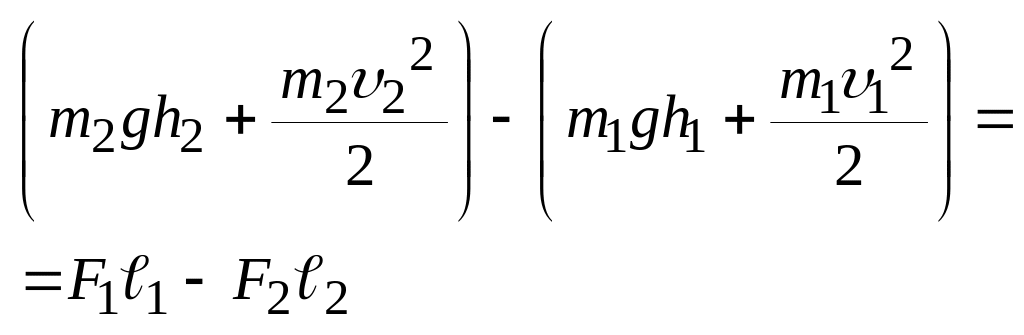
F1=p1S1 F2=p2S2 ℓ1=υ1t ℓ2= υ2t
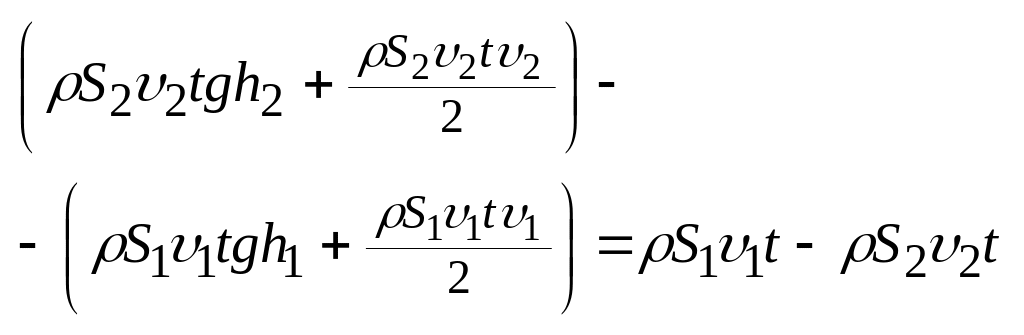 υ1S1=υ2S2
υ1S1=υ2S2
![]()
![]() -
Уравнение Бернулли
-
Уравнение Бернулли
P – статическое давление
ρgh – гидростатическое давление жидкости
![]() -
гидростатическое давление
-
гидростатическое давление
