Условия коллинеарности двух векторов

Пусть вектор коллинеарен вектору , тогда по теореме ( ) имеем = , = , из этих равенств находим , то есть ; ; = , приравниваем левые части этих равенств условие коллинеарности векторов.

Правило. Если векторы коллинеарны , то их координаты пропорциональны.

Определение. Единичный вектор , направленный по вектору , называется его ортом и обозначается

Пример. Найти орт вектора

Решение. Найдём модуль вектора , тогда орт вектора запишется = { } .

Деление отрезка в данном отношении

Определение. Разделить отрезок в данном отношении это значит найти на данном отрезке такую точку М , что имеет место равенство или М₁М .

Пусть даны точки и , найдём координаты точки М (x , y, z ) , делящей отрезок ₂ в отношении .

Z М₁ М = { x - x₁ , y – y₁ , z – z₁ } ;

M₂ = { x₂ – x , y₂ – y , z₂ – z }.

x o y по теореме ( ) в координатах

x – x₁ = (x₂ – x) x (1+ )= x₂ +x₁ x = y – y₁ = ( y₂ – y ) y (1+ ) = y₂ + y₁ y =

z – z₁ = ( z₂ – z ) z (1+ ) = z₂ + z₁ z =

Если точка М середина отрезка , то М₁ М = М М₂ и = 1 , тогда

X_cp. = , Y_cp. = , Z_cp. = .

Если < 0 , то точка М лежит вне отрезка М₁ М₂ .

26

ЛЕКЦИЯ 7. Скалярное произведение векторов. Векторное произведение.

Определение. Скалярным произведением векторов и называется число, равное произведению модулей этих векторов на косинус угла между ними.

Обозначается ( =

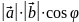
Физический смысл скалярного произведения

И з физики известно , что работа силы по перемещению , находится по формуле А = F S F

S

Если вектор силы , а вектор перемещения , то работа А = = = ( , то есть работа равна скалярному произведению векторов силы и пути

Свойства скалярного произведения

1. ( следует из определения;

2. ( ;

3. ( = ( ;

4.Если , так как ;

5. ( ⁰ ( ² или

6. ( =

7. ( ) =

Выражение скалярного произведения

через координаты перемножаемых векторов

Пусть вектор а вектор , найдём их скалярное произведение ( = = = { ( = =1, другие ска-

27

лярные произведения базисных векторов равны нулю, так как они взаимно перпендикулярны } = .

Запишем основные формулы в декартовых координатах :

п = ; ;

→ условие перпендикулярности 2-х векторов.

Пример. Найти работу силы по перемещению в направлении вектора

Решение. А = ( .

Векторное произведение векторов

Правые и левые тройки векторов

Определение. Тройка векторов называется правой ( левой ) , если после приведения к одному началу , вектор располагается по ту сторону плоскости , определяемой векторами откуда поворот от к свершается против часовой стрелки ( по часовой стрелки).

Левая Правая

Определение. Аффинная система координат называется правой ( левой ) , если три базисных вектора образуют правую ( левую ) тройку.

Определение. Векторным произведением вектора на вектор называется вектор , который удовлетворяет 3- м условиям:

1). ;

2). Вектор и ;

3). Вектор направлен так , что образует правую тройку с векторами и ;

Обозначается или .

Свойства векторного произведения

1. [ антикоммутативно;

2. [ = [ = [ 3. [ + ) ]= [ + [ ;

28

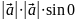4. Если и коллинеарны,то [ = 0 или [ , так как = = 0 ;

5.Модуль векторного произведения равен площади параллелограмма, построенного на векторах сомножителях .

S ={ из школы известно} = =

S = S = .

Физический смысл векторного произведения

1) . Рассмотрим физическую задачу.

Пусть твёрдое тело вращается с угловой скоростью вокруг неподвижной оси.

М – произвольная точка , - линейная скорость ,

z направленная по касательной к окружности ,

описываемой точкой М.

ddD , ⊥ оси oz , из треугольника

OO₁M , тогда так как ⊥ и , а поворот от к против ча

совой стрелки , то линейную скорость можно рас-

y сматривать как векторное произведение , то есть

x Вывод: векторное произведение угловой скорос - ти на радиус – вектор произвольной точки вращающегося тела есть линейная скорость.

M M ]

2) . Можно показать , что вращающий момент силы , приложенной к точке В тела есть векторное произведение вектора –плеча на вектор-силы.

A

AAA

B