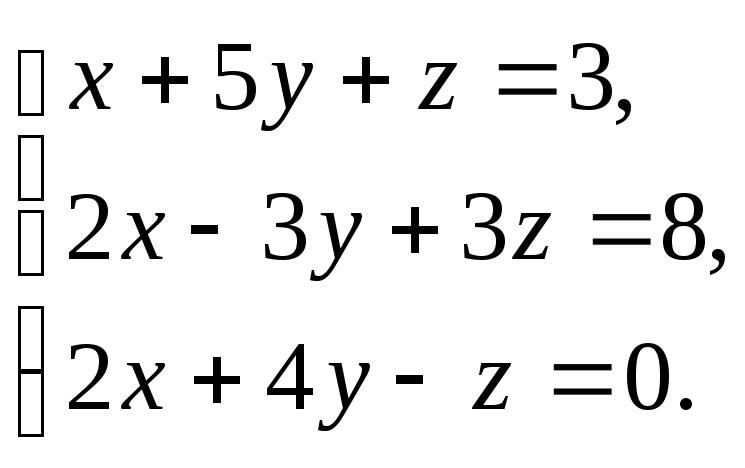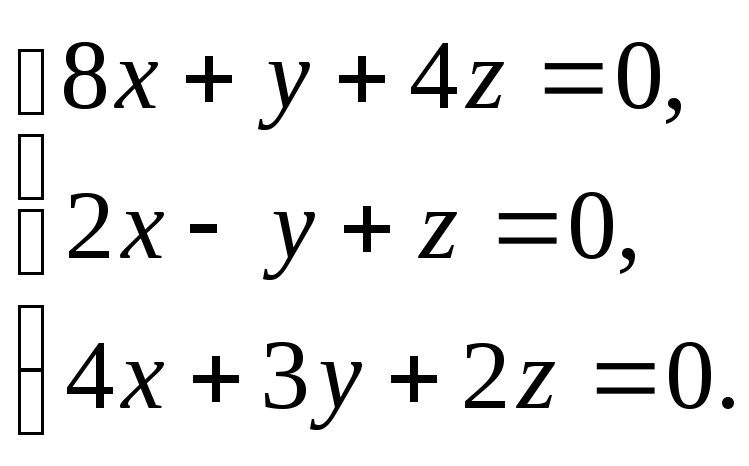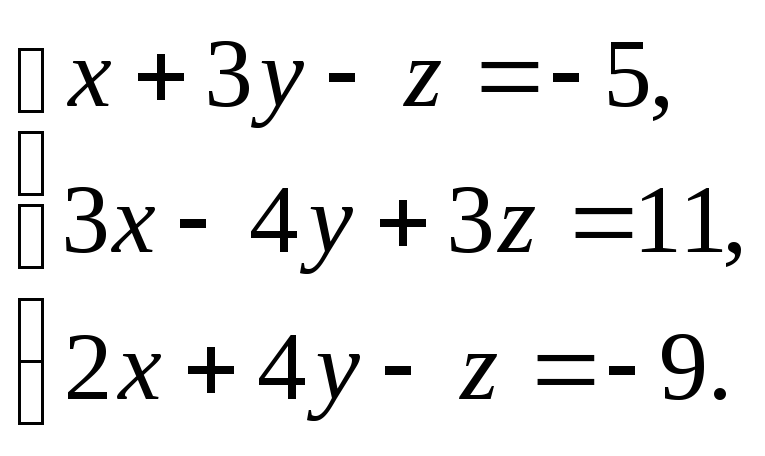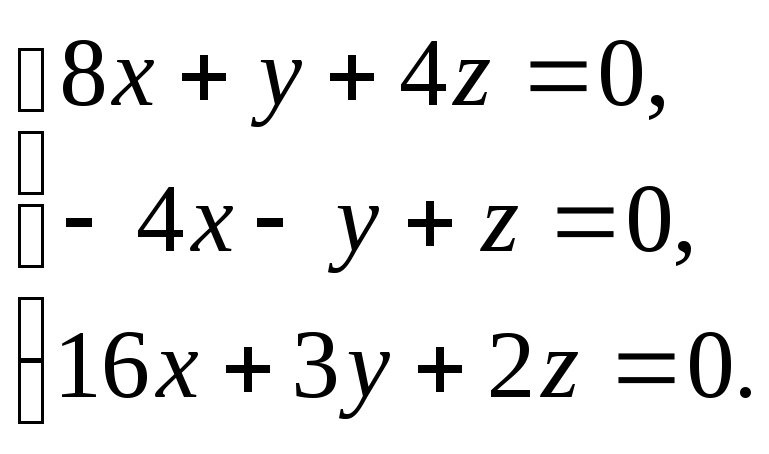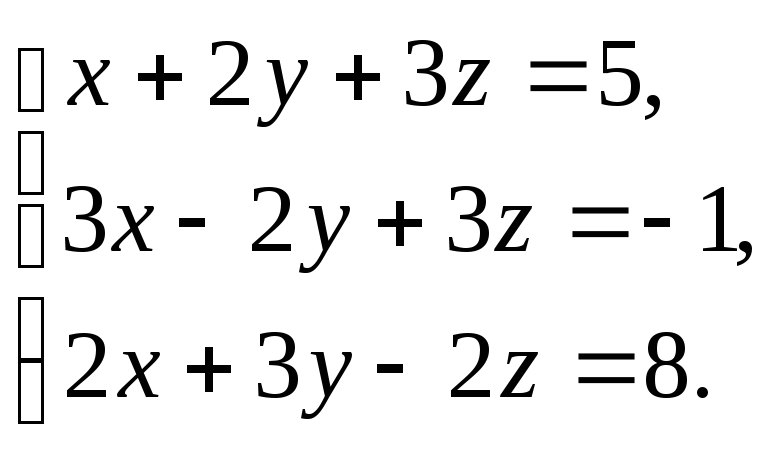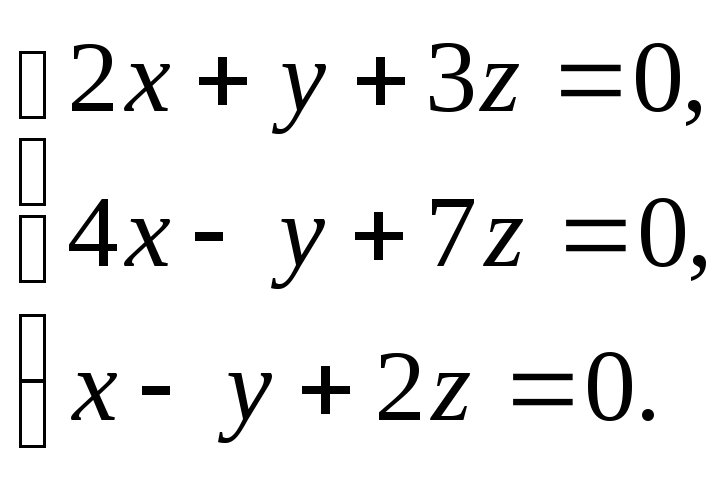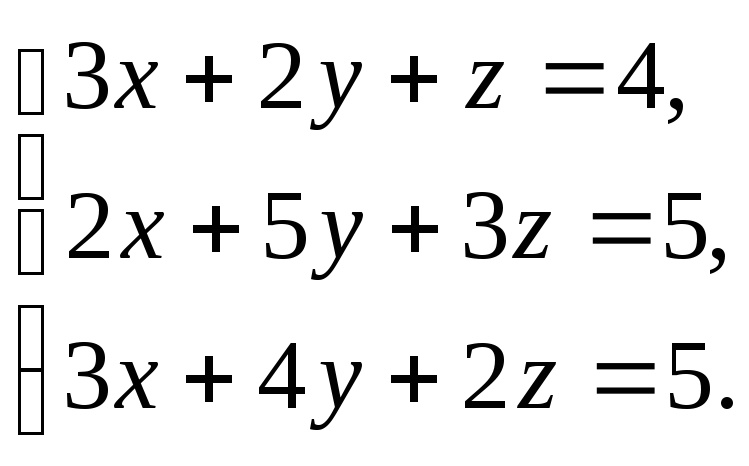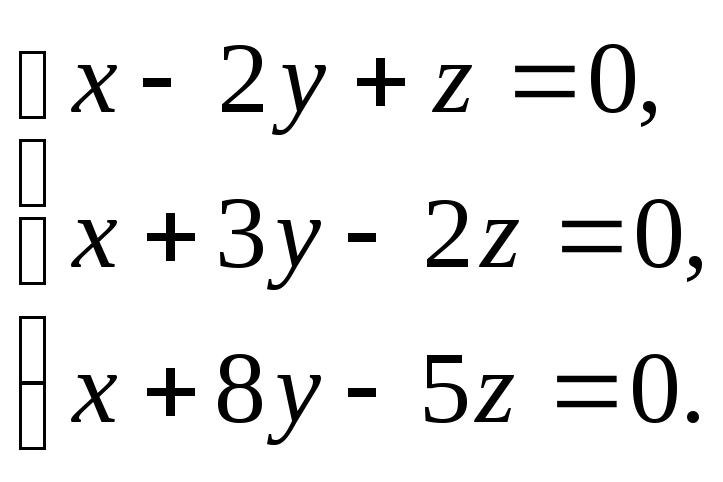|
Вариант
1.
-
Дано:
вектор ā=20i+30j-60k. Найти длину вектора
 и направление.
и направление.
-
Дано:
модуль вектора
 равен 3, модуль вектора
равен 3, модуль вектора
 равен 4, угол между векторами
равен 4, угол между векторами
 и и
 равен 120º. Найти модуль вектора
равен 120º. Найти модуль вектора
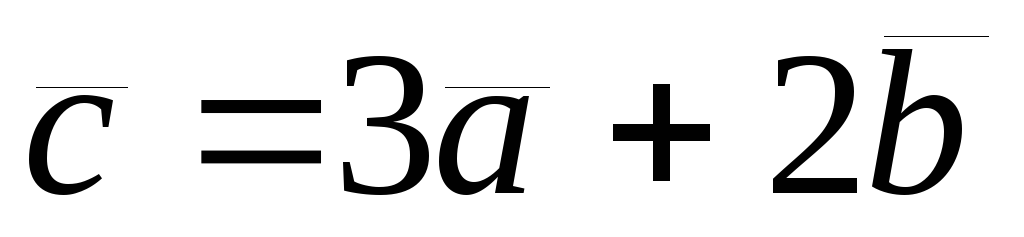 . .
-
Найти
произведение матриц АВ:
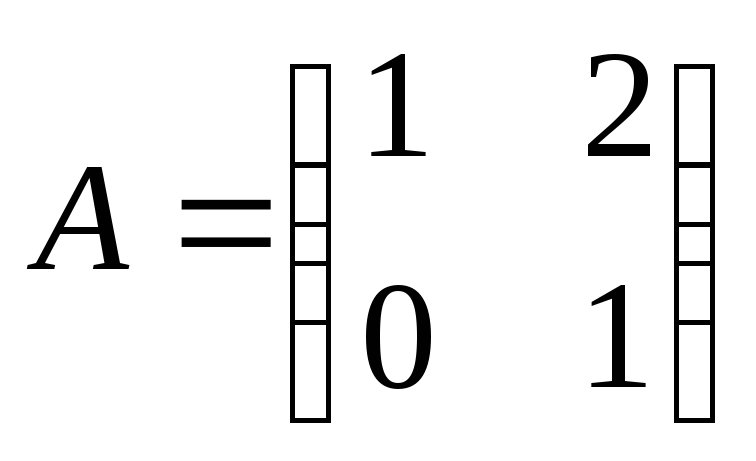 , ,
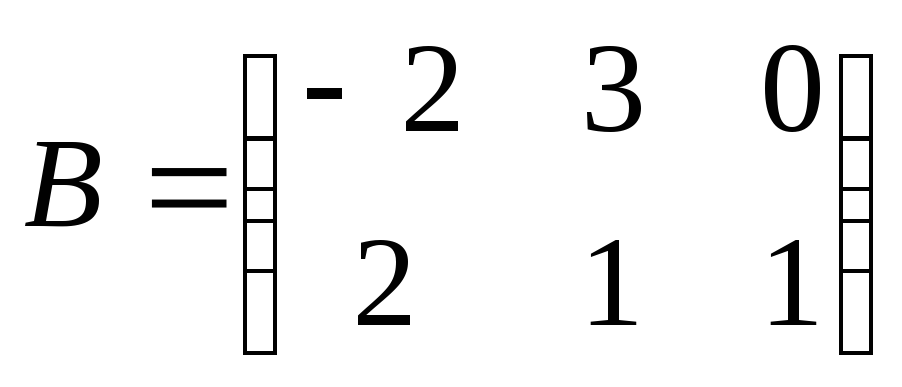 . .
-
Вычислить
определитель второго порядка
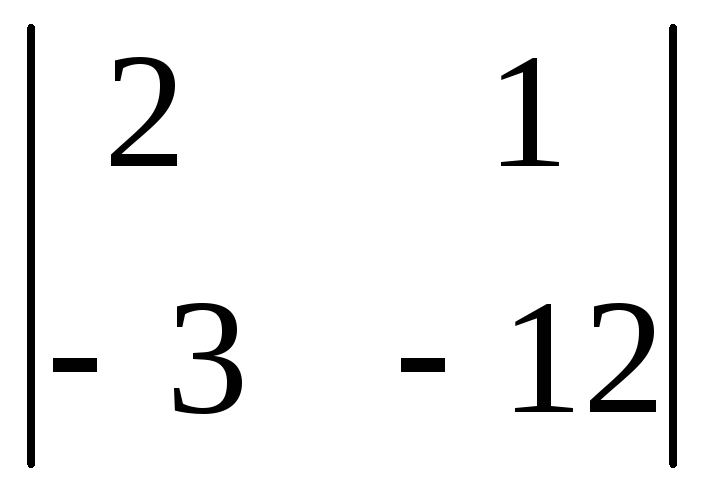 . .
-
Решить
систему:
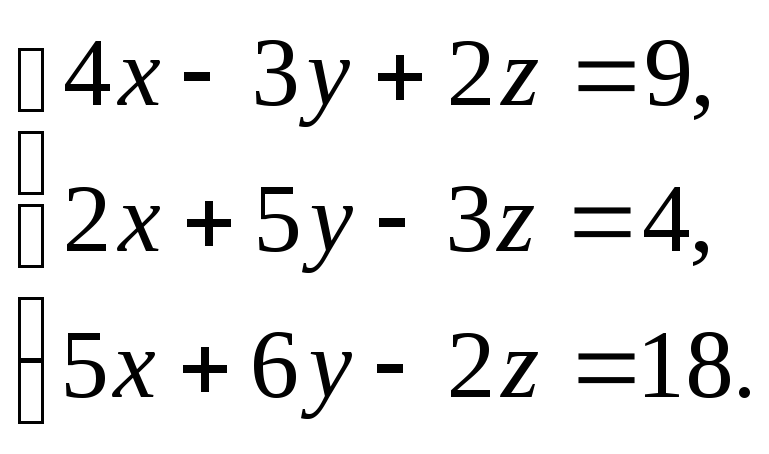
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
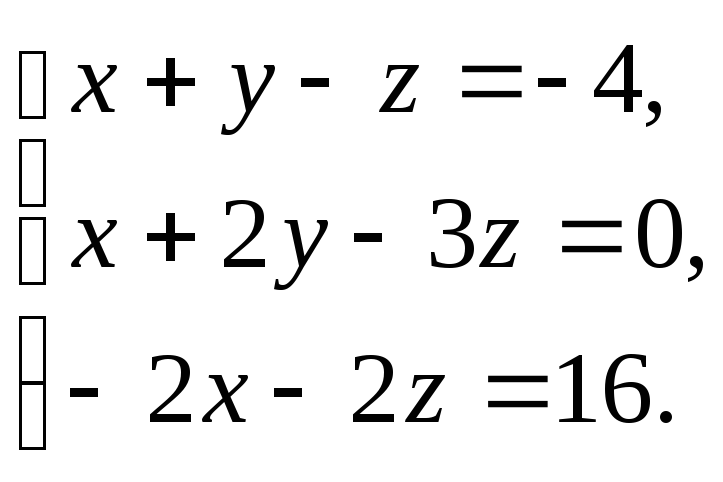
|
|
Вариант
2.
-
Дано:
т.А(1, 3, 2), т.В(5, 8, 1). Найти длину вектора
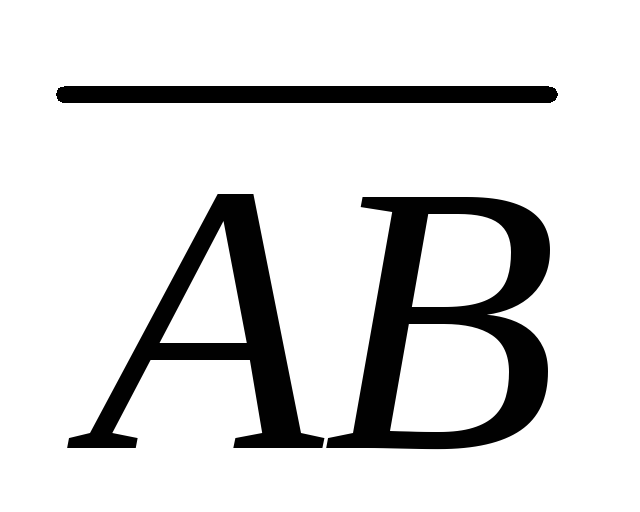 . .
-
Определить
угол между векторами ā=i+2j+3k и
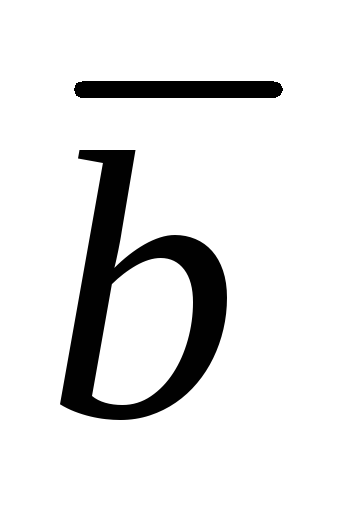 =6i+4j-2k. =6i+4j-2k.
-
Найти
произведение матриц АВ:
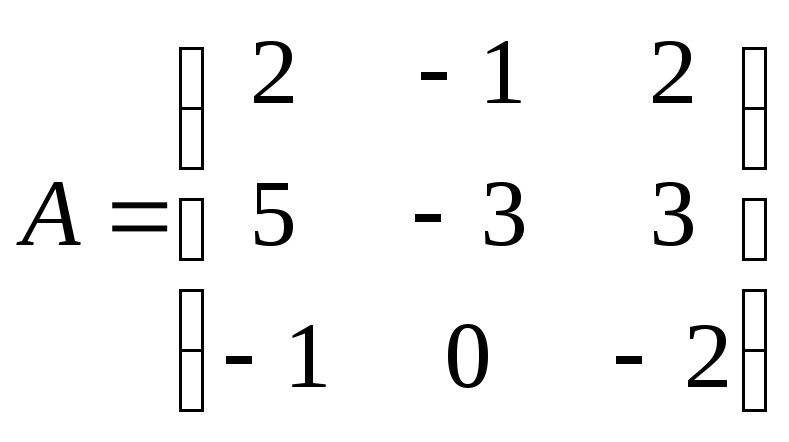 , ,
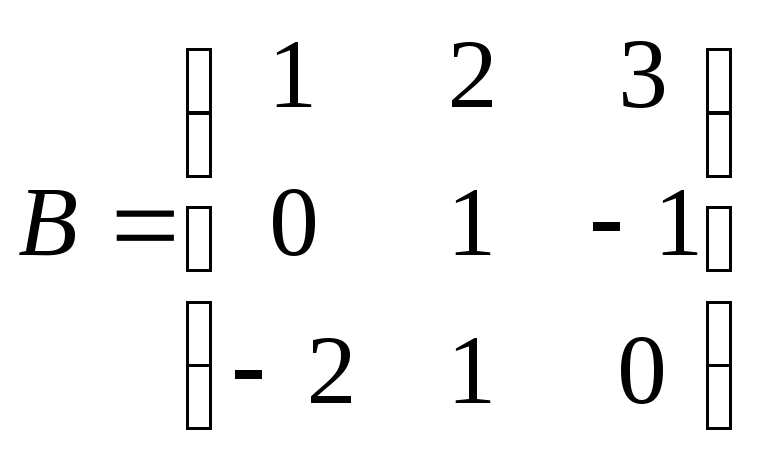 . .
-
Вычислить
определитель второго порядка
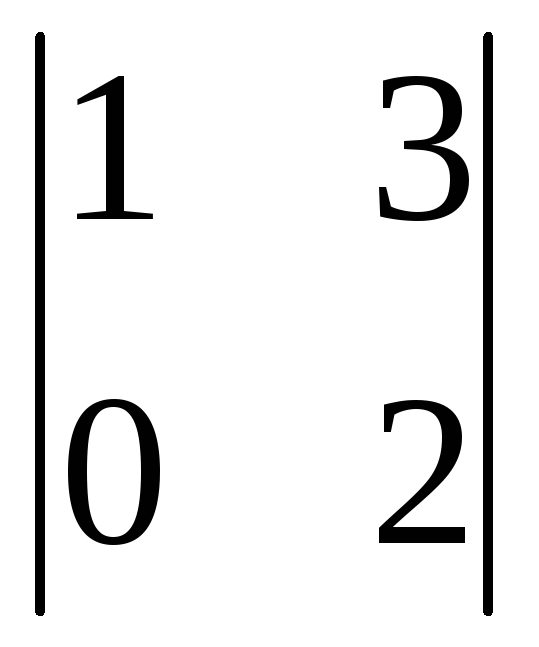 . .
-
Решить
систему:

-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
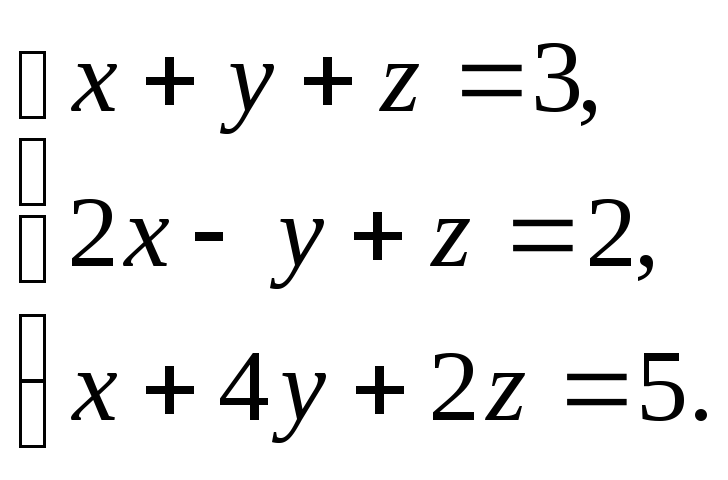
|
|
Вариант
3.
-
Дано:
т.А(0, 0, 1), т.В(3, 2, 1), т.С(4, 5, 6), т.D(1,
6, 3). Найти координаты вектора
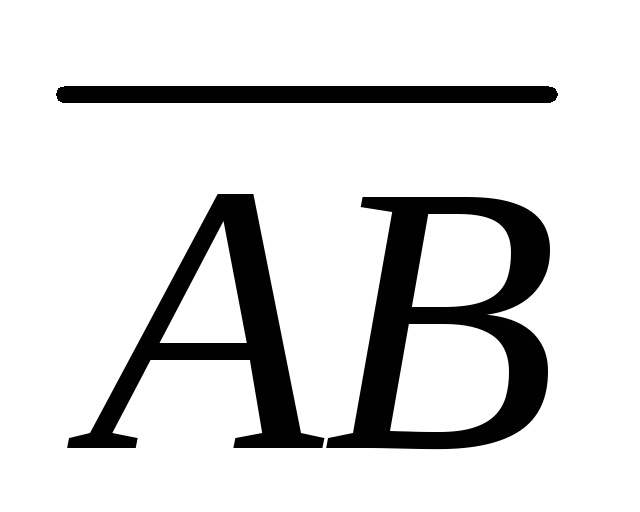 +
+
 . .
-
Найти
скалярное произведение векторов
ā=3i+4j+7k и
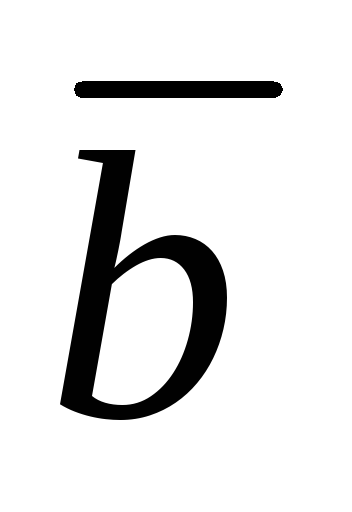 =2i-5j+2k. =2i-5j+2k.
-
Найти
произведение матриц АВ:
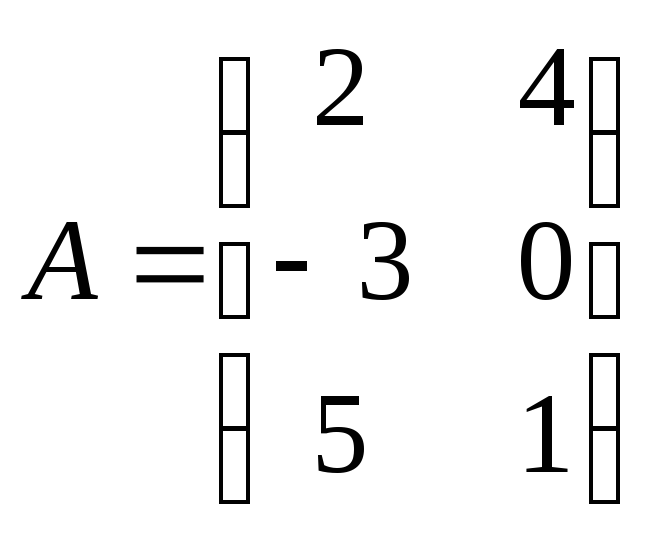 , ,
 . .
-
Вычислить
определитель второго порядка
 . .
-
Решить
систему:
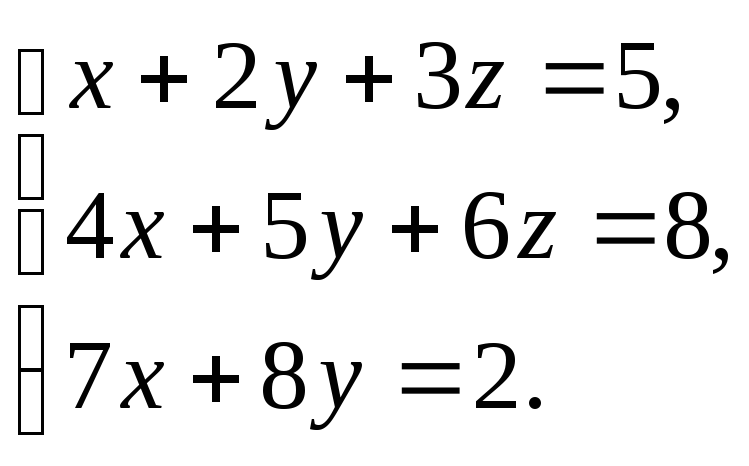
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
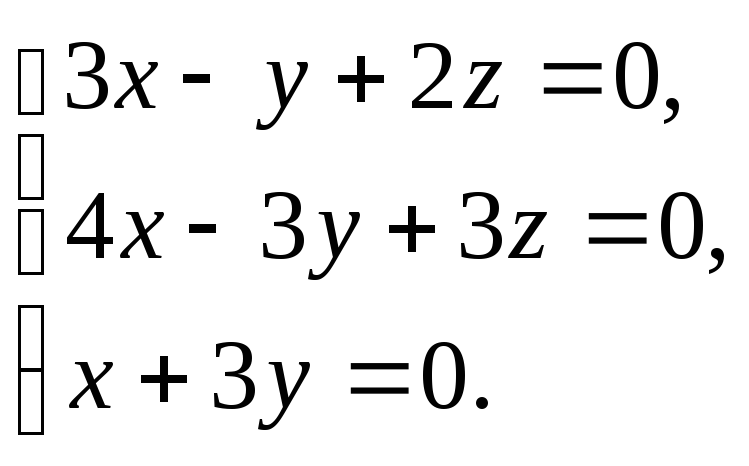
|
|
Вариант
4.
-
Вычислить
модуль вектора ā=i+2j+k и найти его
направление.
-
Найти
скалярное произведение векторов
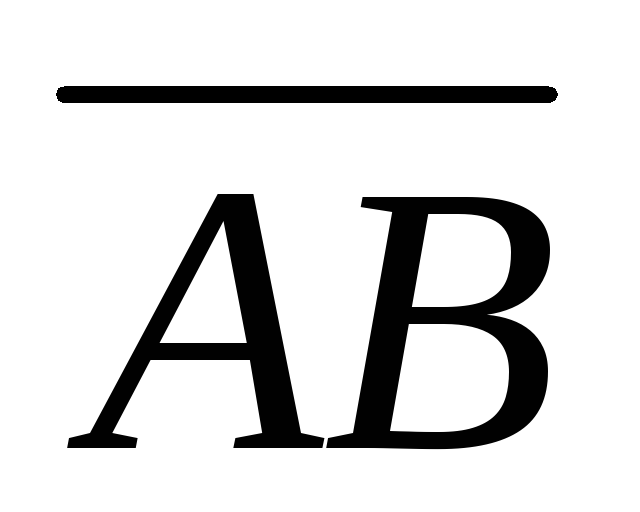 и
и
 ,
если т.А(1, 0, 1), т.В(4, 2, 0), т.С(4, 0, 6), т.D(1,
2, 3). ,
если т.А(1, 0, 1), т.В(4, 2, 0), т.С(4, 0, 6), т.D(1,
2, 3).
-
Найти
произведение матриц АВ:
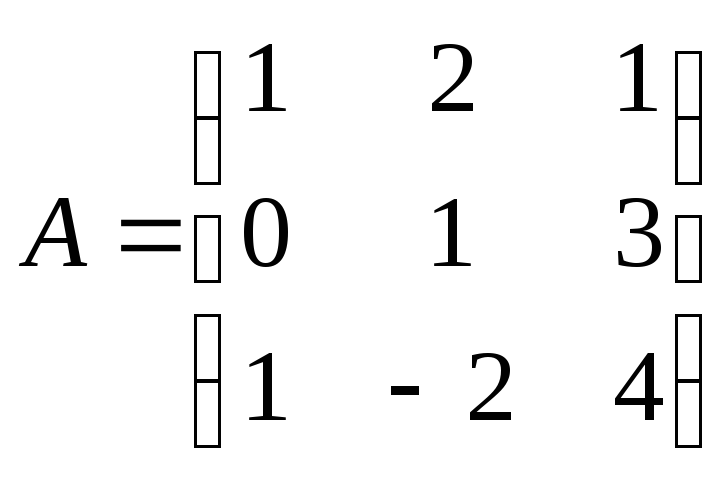 , ,
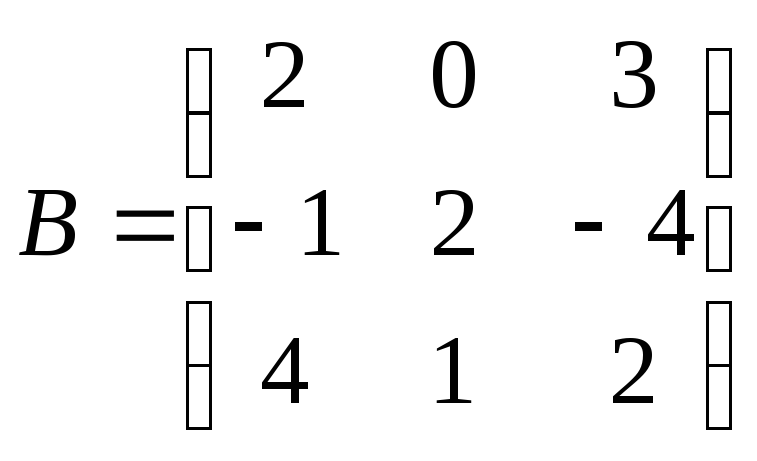 . .
-
Вычислить
определитель второго порядка
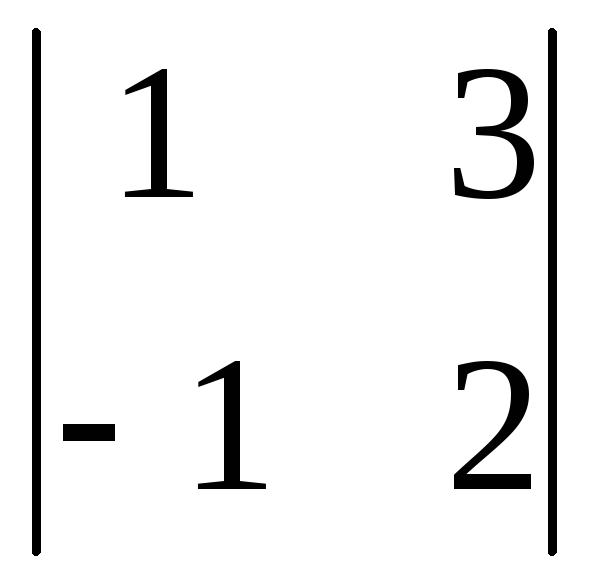 . .
-
Решить
систему:
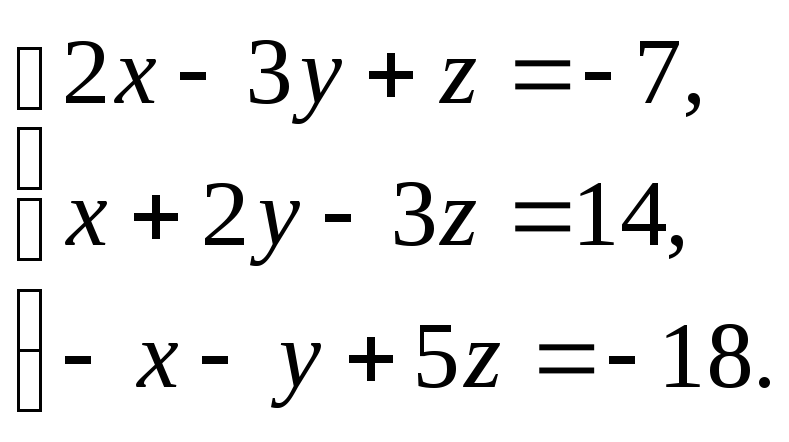
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
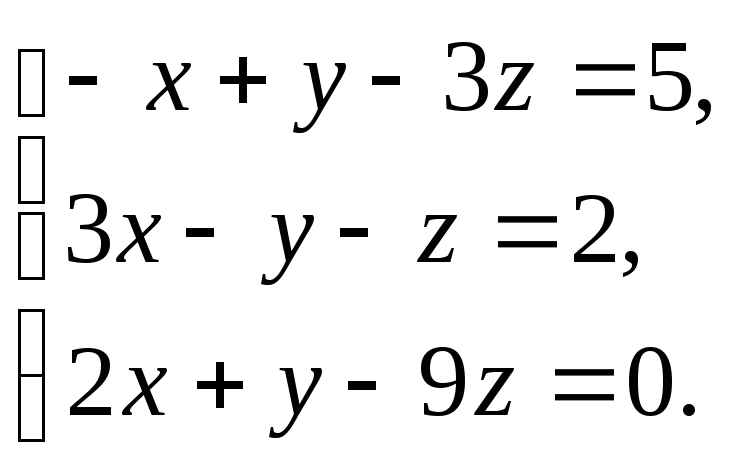
|
|
Вариант
5.
-
Дано:
вектор ā=3i+4j-12k. Найти длину вектора ā
и направление.
-
Дан
треугольник с вершинами А(2, 2, 2), В(4,
0, 3), С(0, 1, 0). Найти угол при вершине В.
-
Найти
произведение матриц АВ:
 , ,
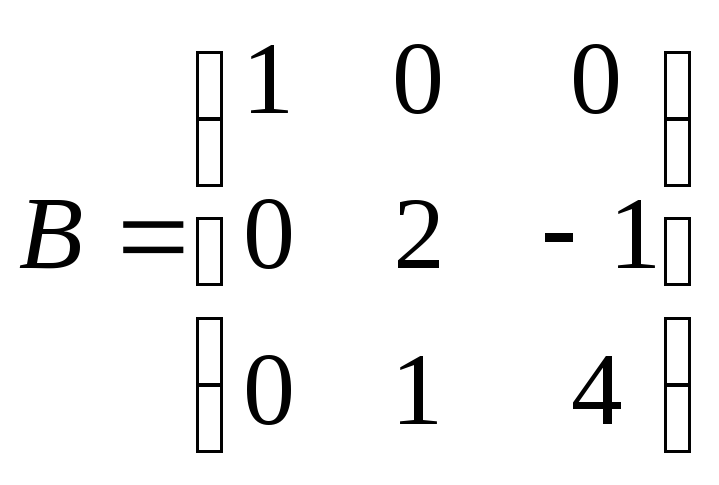 . .
-
Вычислить
определитель второго порядка
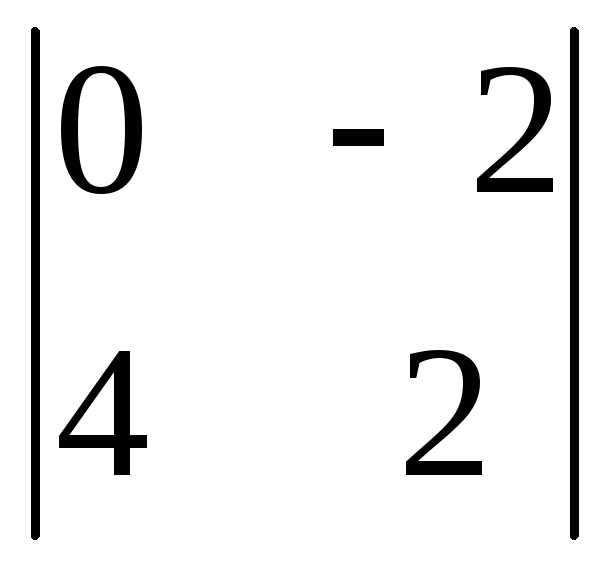 . .
-
Решить
систему:
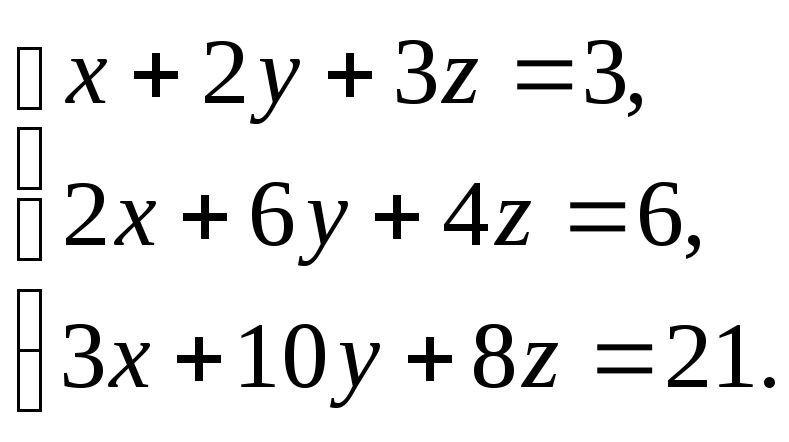
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
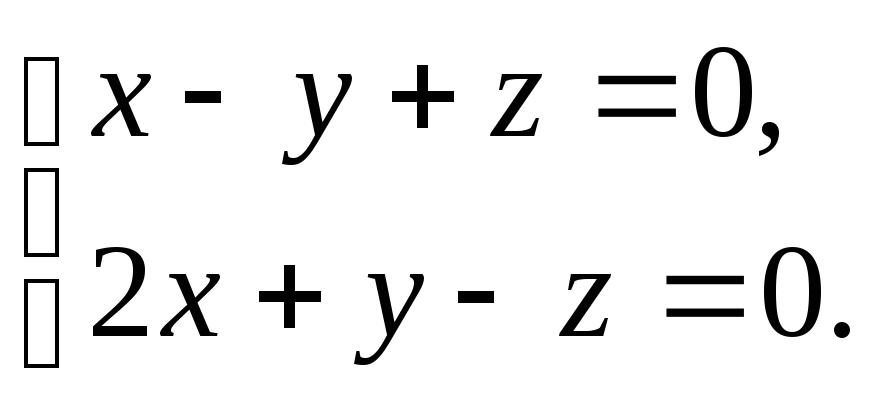
|
|
Вариант
6.
-
Найти
длину вектора
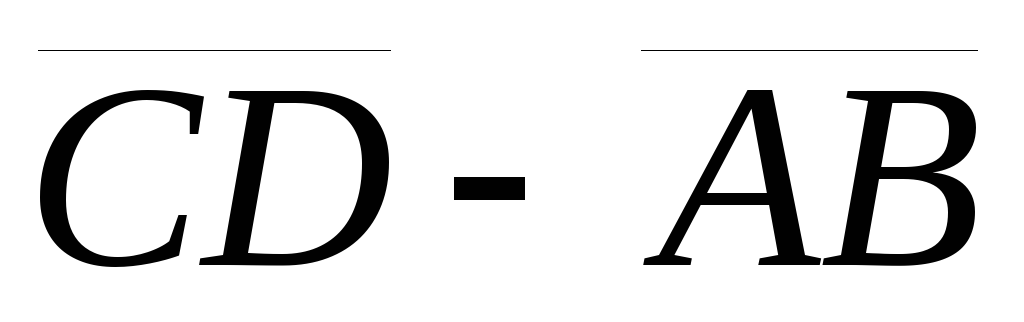 ,
если т.А(1, 2, 1), т.В(2, 2, 4), т.С(1, 2, 6), т.D(1,
3, 4). ,
если т.А(1, 2, 1), т.В(2, 2, 4), т.С(1, 2, 6), т.D(1,
3, 4).
-
Дано:
вектор
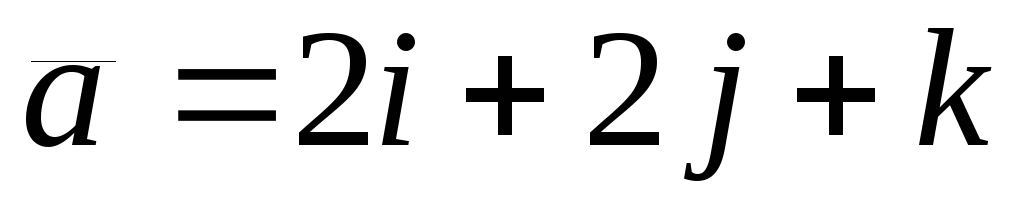 ,
вектор ,
вектор
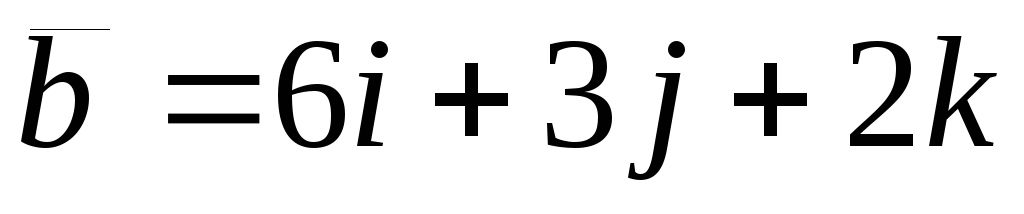 .
Найти проекцию вектора .
Найти проекцию вектора
 на вектор
на вектор
 . .
-
Найти
произведение матриц ВА:
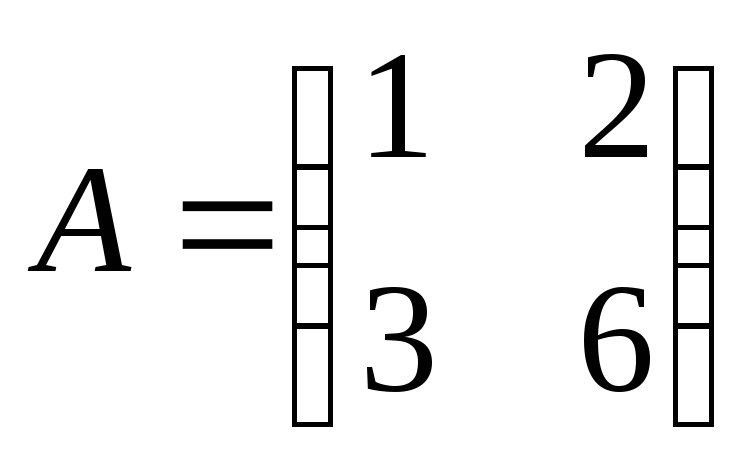 , ,
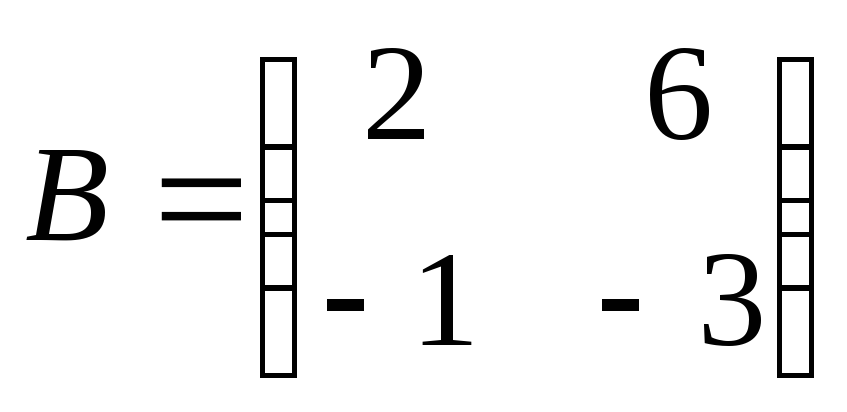 . .
-
Вычислить
определитель второго порядка
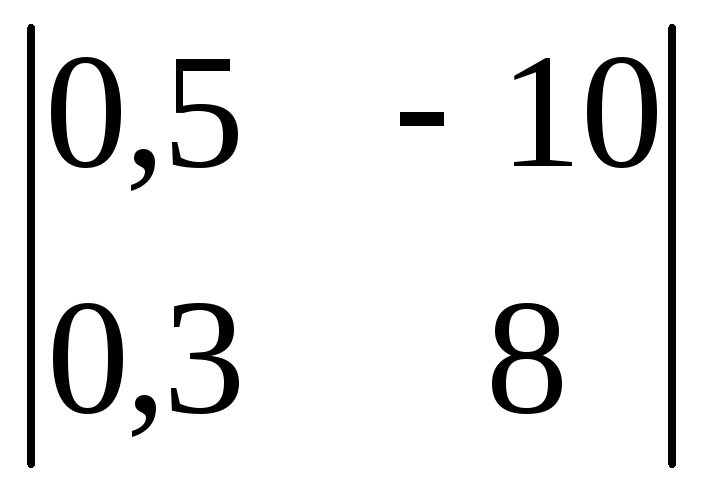 . .
-
Решить
систему:
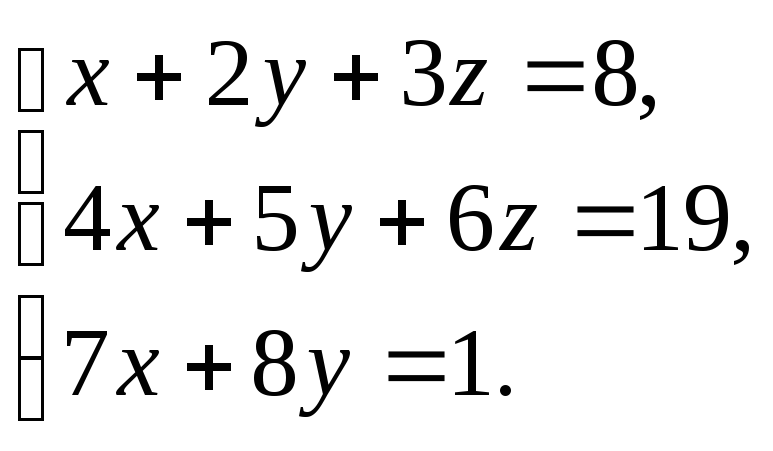
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
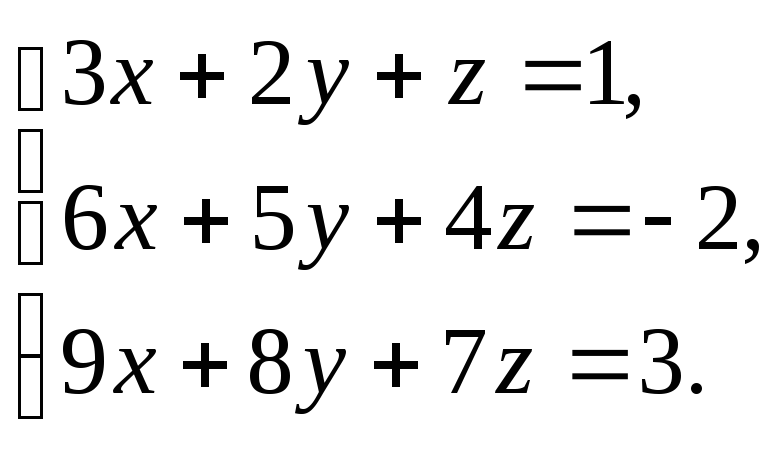
|
|
Вариант
7.
-
Дано:
т.А(1, 3, 2), т.В(3, -4, 6). Найти длину и
направление вектора
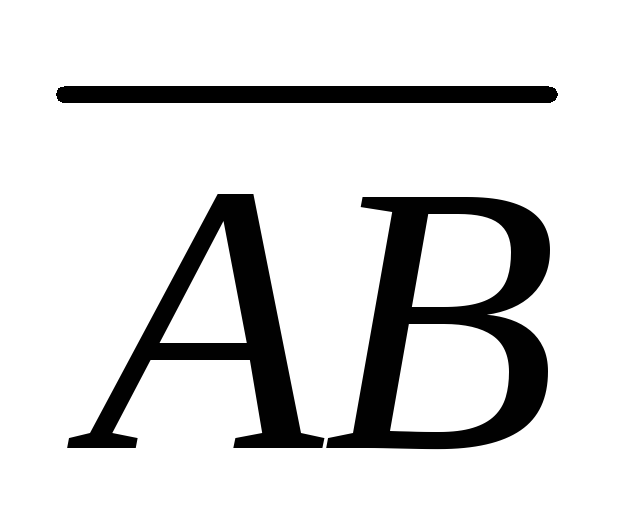 . .
-
Определить
угол между векторами
 =2i+5j+k
и =2i+5j+k
и
 =i+2j–3k. =i+2j–3k.
-
Найти
произведение матриц ВА:
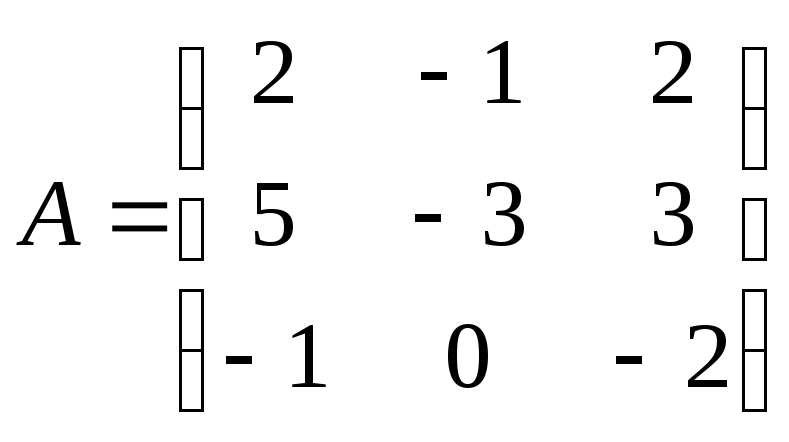 , ,
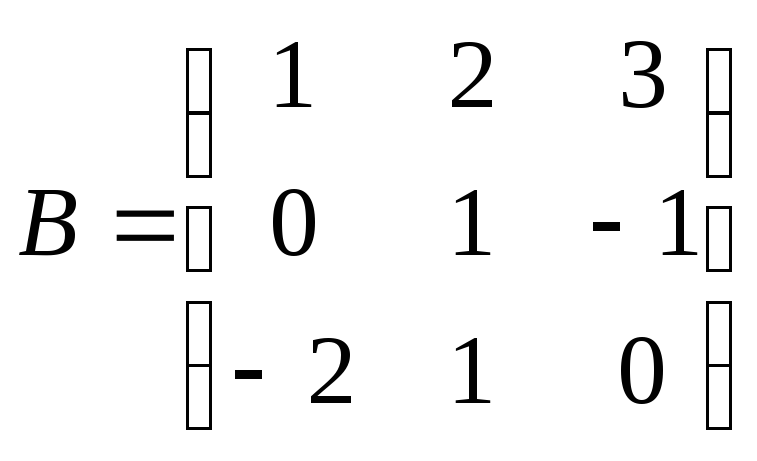 . .
-
Вычислить
определитель второго порядка
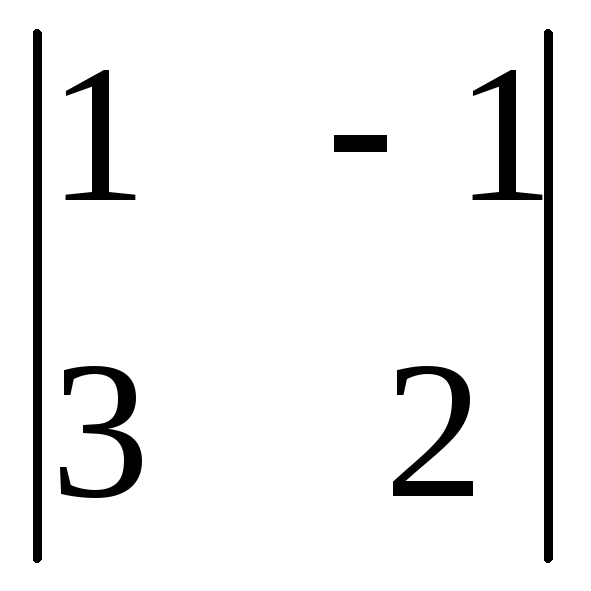 . .
-
Решить
систему:
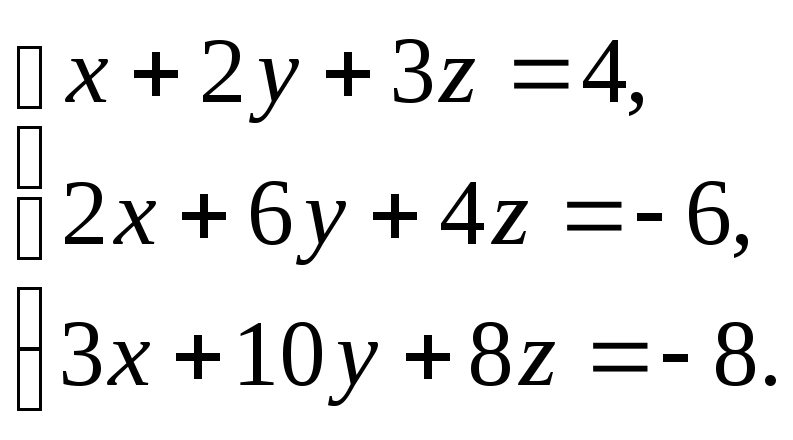
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
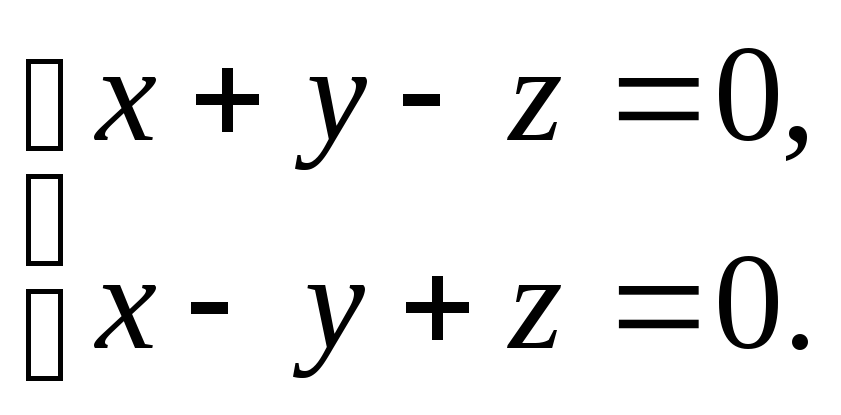
|
|
Вариант
8.
-
Найти
длины сторон треугольника с вершинами
А(1, 1, 1), В(2, 3, 4), С (4, 3, 2).
-
Найти
скалярное произведение векторов
ā=2i+3j+5k и
 =i+2j+5k. =i+2j+5k.
-
Найти
произведение матриц АВ:
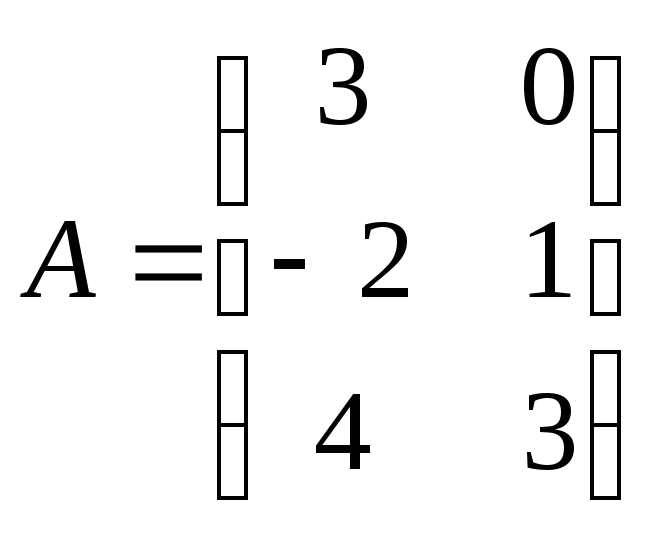 , ,
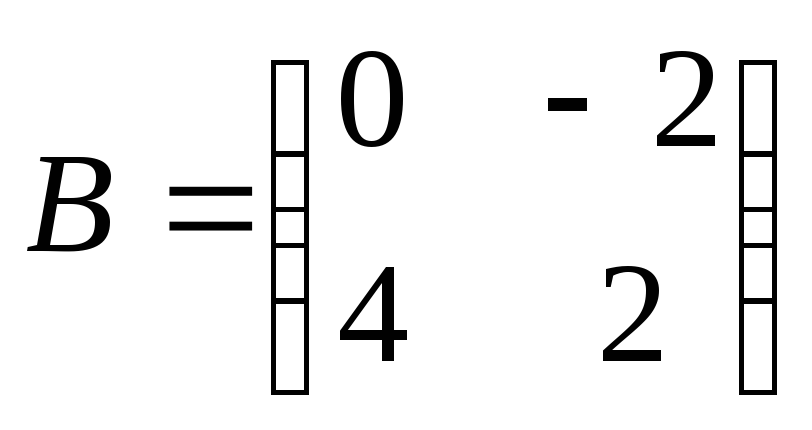 . .
-
Вычислить
определитель второго порядка
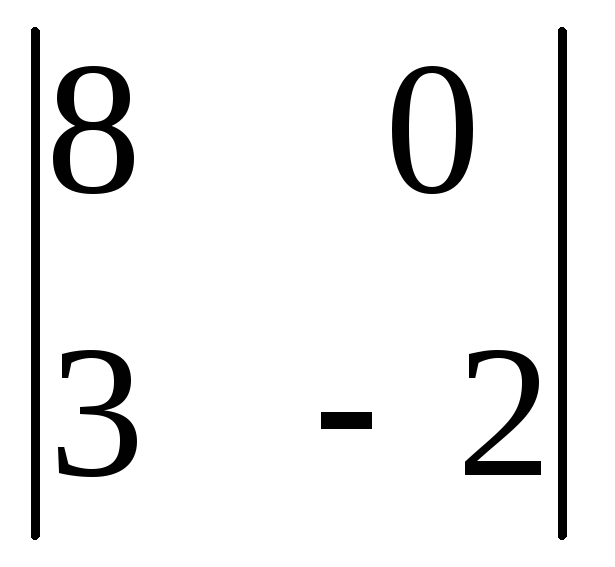 . .
-
Решить
систему:
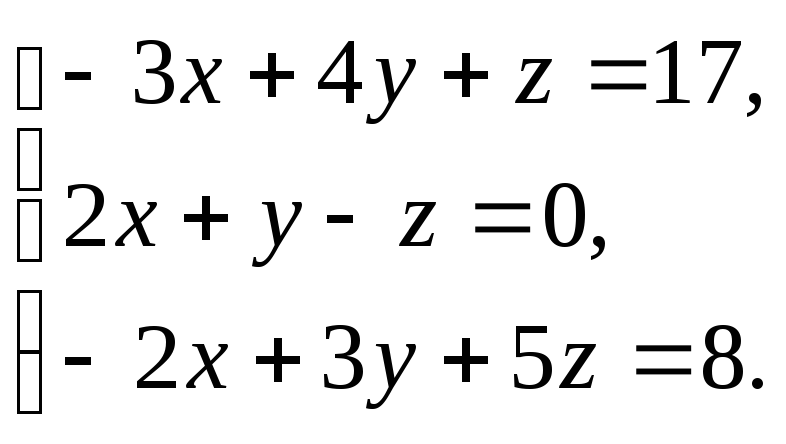
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
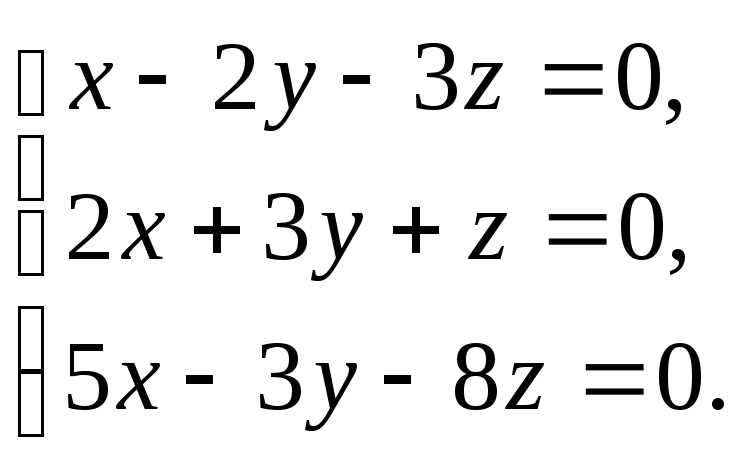
|
|
Вариант
9.
-
Найти
длину вектора
 + + ,
если ā=2i–j–k, ,
если ā=2i–j–k,
 =i+3j–k. =i+3j–k.
-
Дан
треугольник с вершинами А(2, 1, 0), В(2,
1, 3), С(1, 1, 0). Найти угол при вершине С.
-
Найти
произведение матриц АВ: , ,
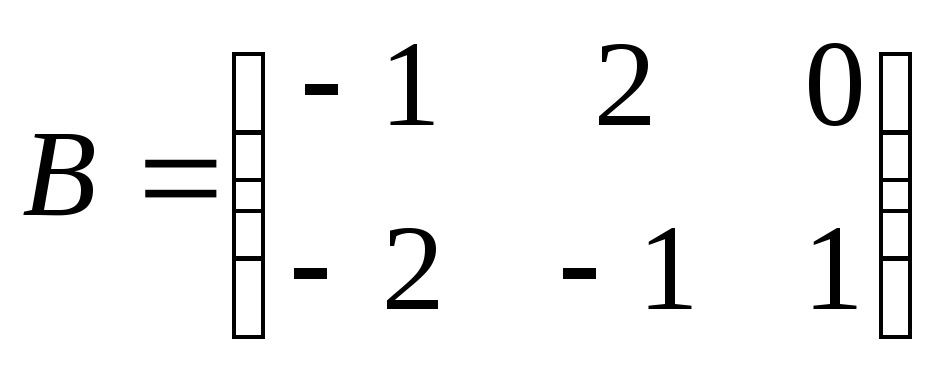 . .
-
Вычислить
определитель второго порядка
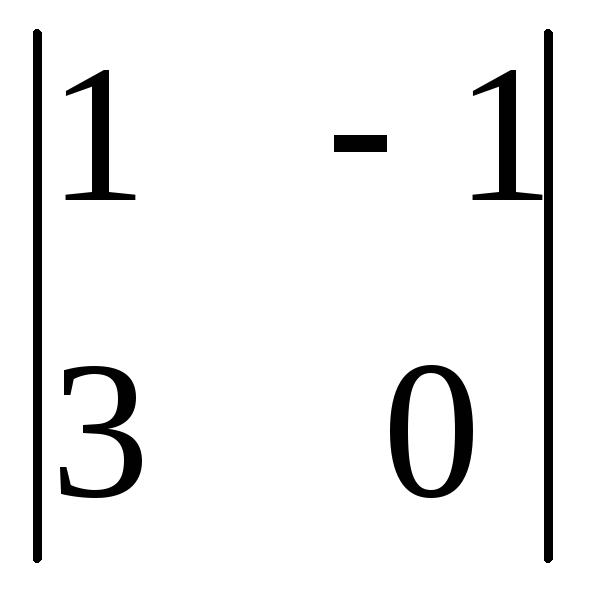 . .
-
Решить
систему:
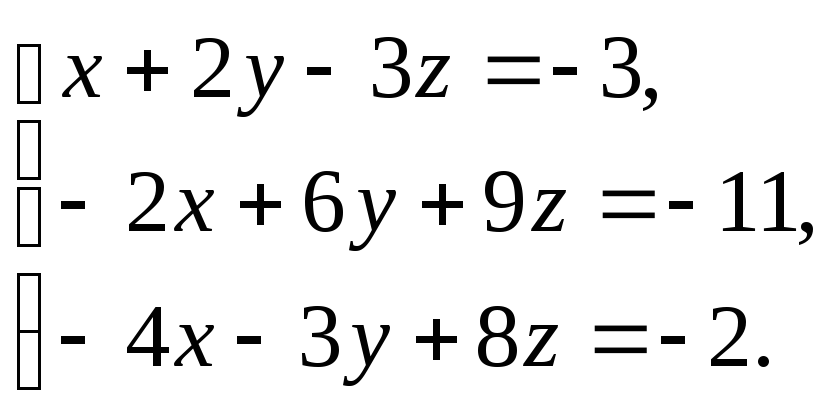
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
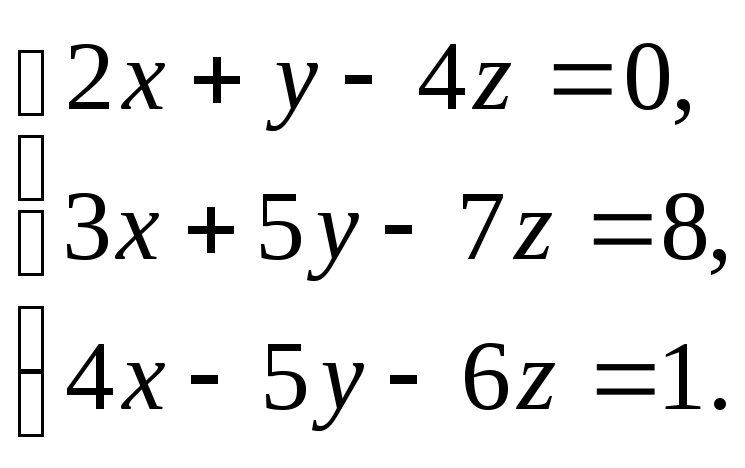
|
|
Вариант
10.
-
Найти
длину вектора 2 – – ,
если ā=i+2j+3k, ,
если ā=i+2j+3k,
 =6i+4j-2k. =6i+4j-2k.
-
Дано:
модуль вектора
 равен 1, модуль вектора
равен 1, модуль вектора
 равен 1, угол между векторами
равен 1, угол между векторами
 и и
 равен 30º. Найти скалярное произведение
равен 30º. Найти скалярное произведение
( +3 +3 ,
3 ,
3 + + ). ).
-
Найти
произведение матриц АВ:
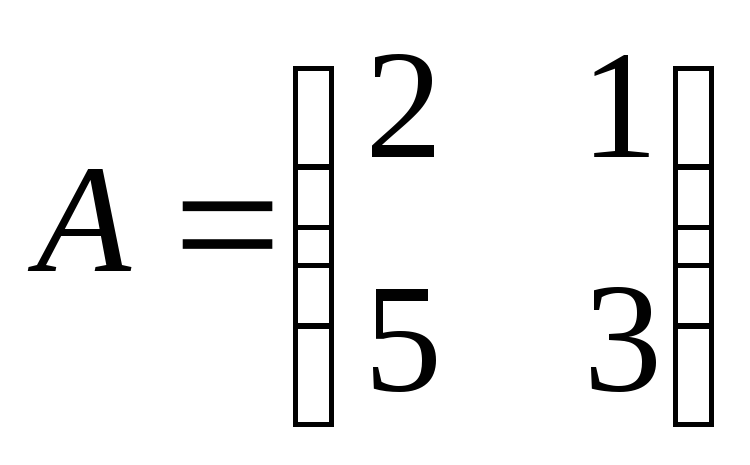 , ,
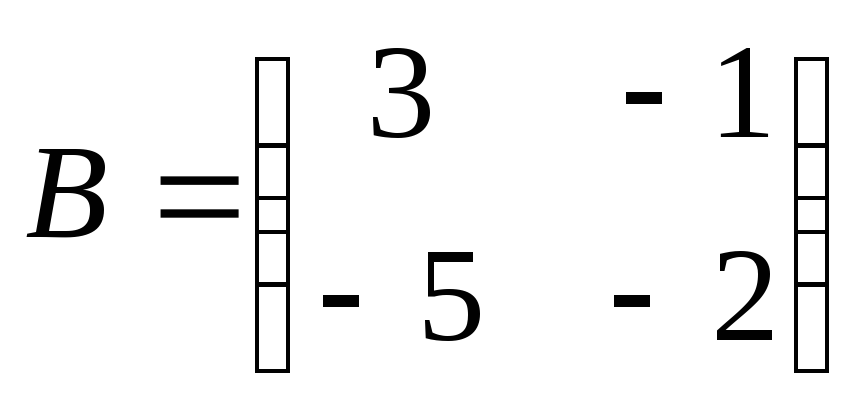 . .
-
Вычислить
определитель второго порядка
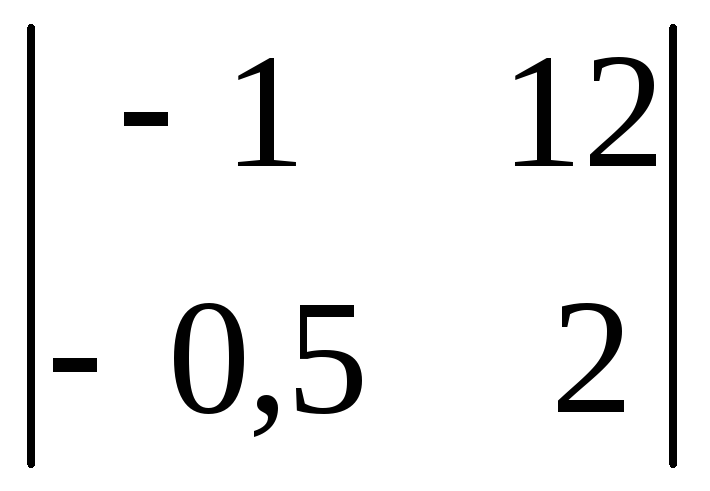 . .
-
Решить
систему:
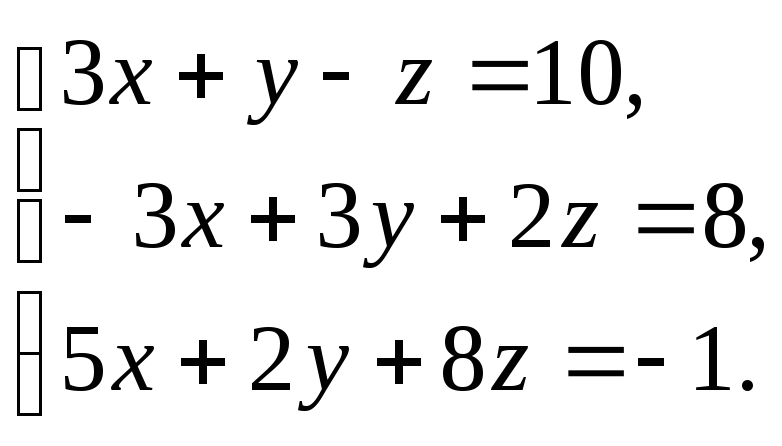
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
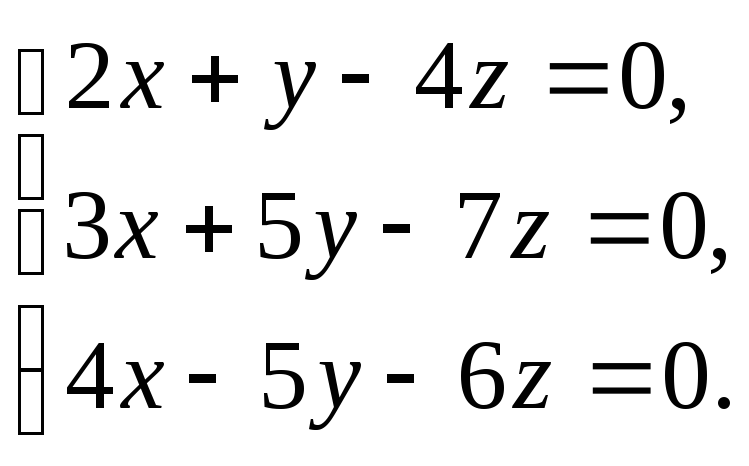
|
|
Вариант
11.
-
Найти
длину вектора
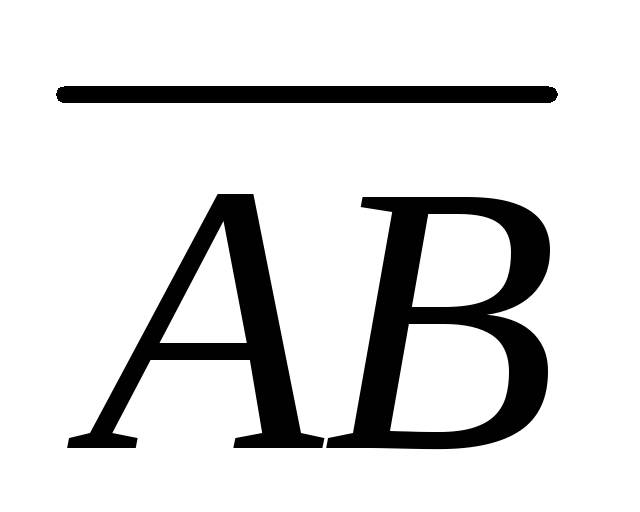 и направление, если А(1, 6, 1), В(3, -1, 5).
и направление, если А(1, 6, 1), В(3, -1, 5).
-
Дано:
вектор
 =7i–3j+2k,
вектор =7i–3j+2k,
вектор
 =3i–7j+8k.
Найти проекцию вектора =3i–7j+8k.
Найти проекцию вектора
 на вектор
на вектор
 . .
-
Найти
произведение матриц АВ:
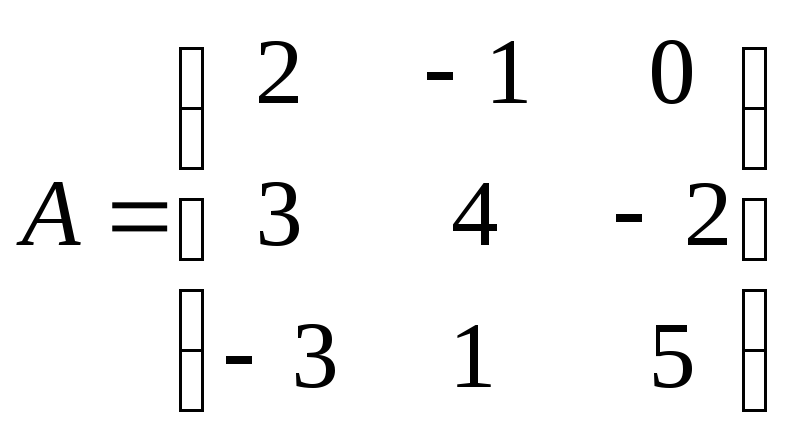 , ,
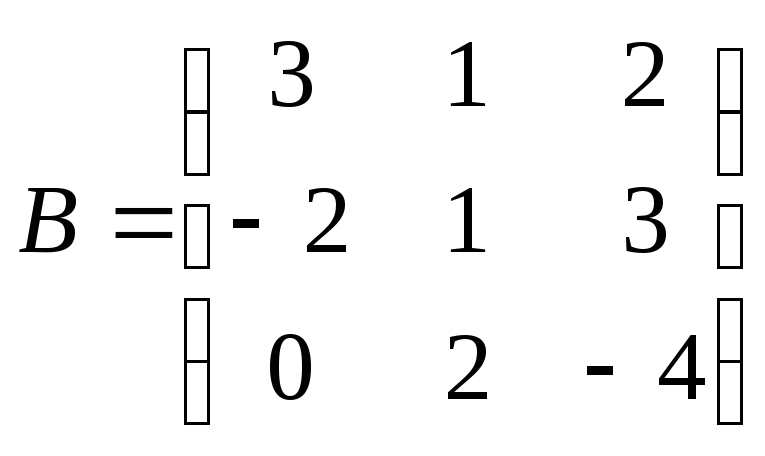 . .
-
Вычислить
определитель второго порядка
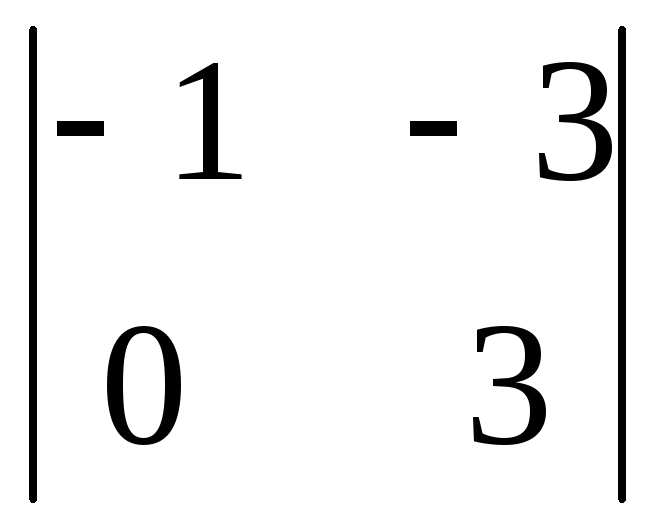 . .
-
Решить
систему:
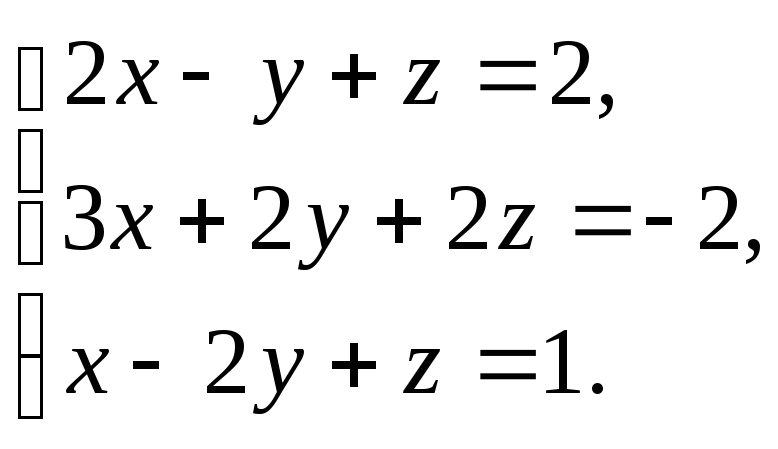
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
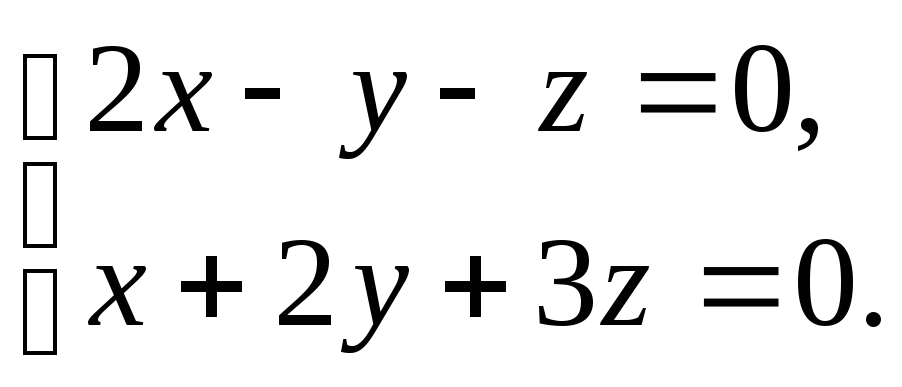
|
|
Вариант
12.
-
Дано:
вектор ā=i-2j-2k. Найти длину вектора ā
и направление.
-
Дан
треугольник с вершинами А(1, 2, 1), В(3,
0, 5), С (2, 0, 1). Найти угол при вершине А.
-
Найти
произведение матриц ВА:
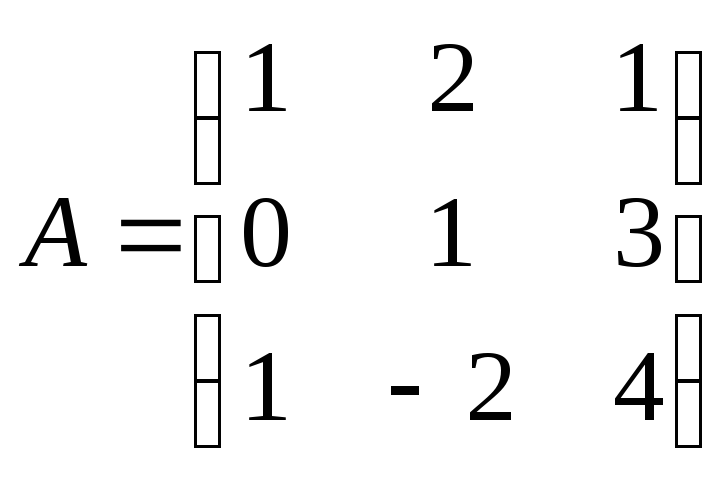 , ,
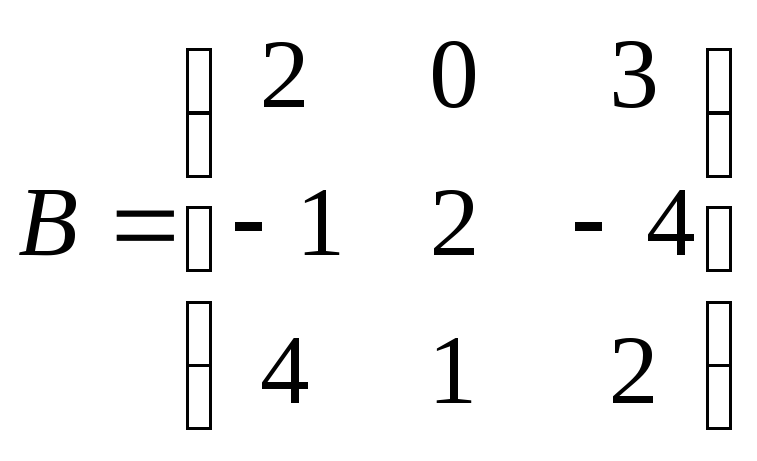 . .
-
Вычислить
определитель второго порядка
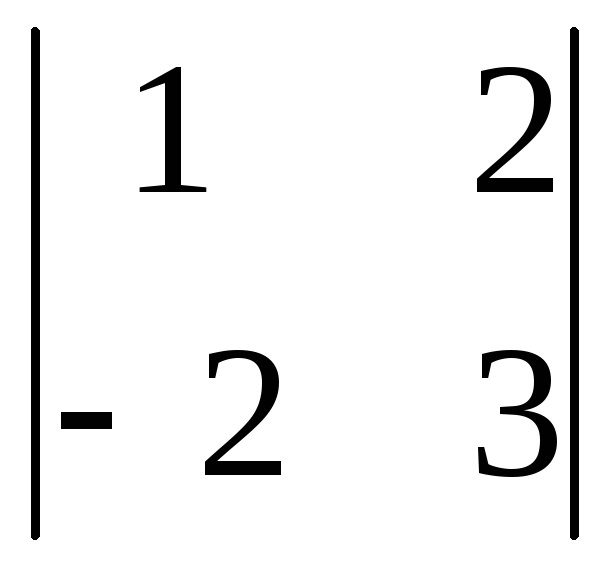 . .
-
Решить
систему:
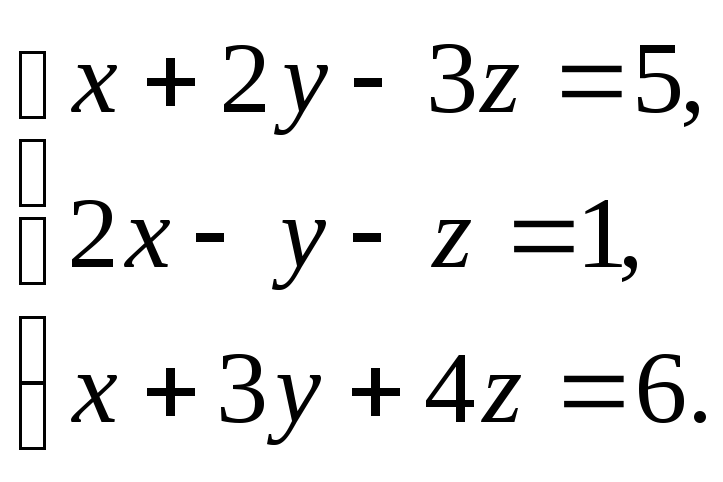
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
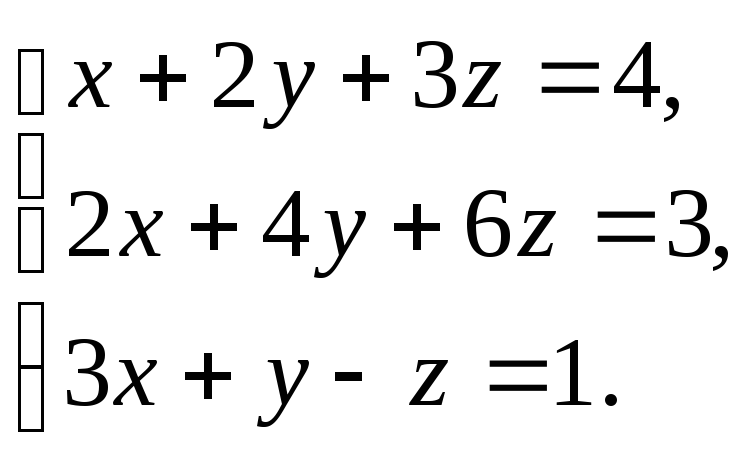
|
|
Вариант
13.
-
Найти
длину вектора
 + +
 ,
если ā=2i–j–k, ,
если ā=2i–j–k,
 =i+j+4k. =i+j+4k.
-
Найти
скалярное произведение (5 +3 +3 ,
2 ,
2 – – ),
если модуль вектора ),
если модуль вектора
 равен 2, модуль вектора
равен 2, модуль вектора
 равен 3,
равен 3,
 и и
 перпендикулярны.
перпендикулярны.
-
Найти
произведение матриц ВА:
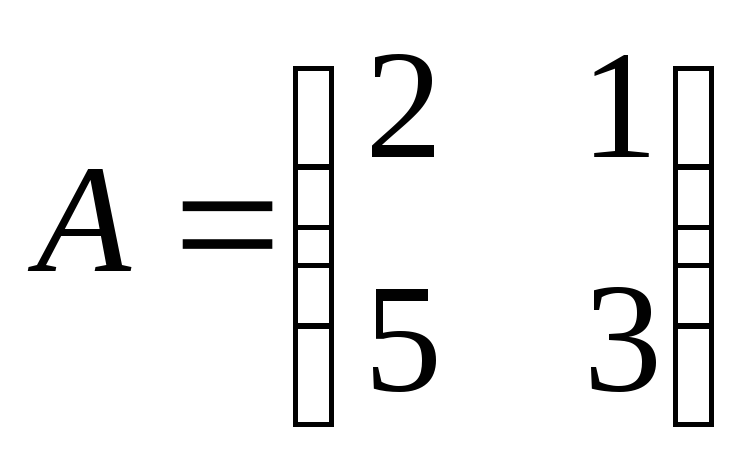 , ,
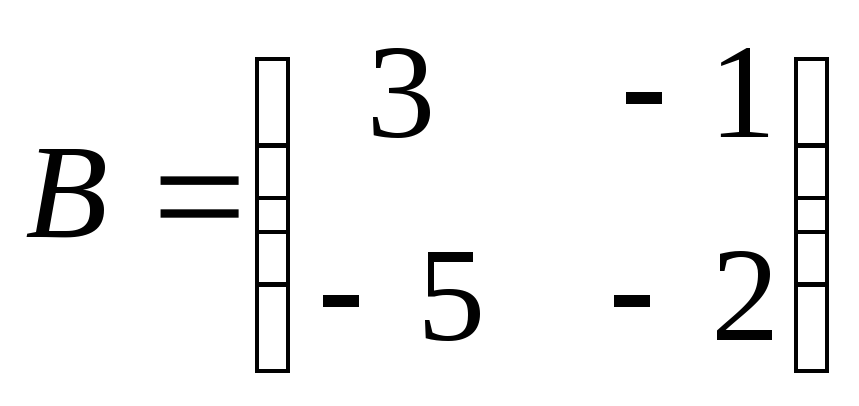 . .
-
Вычислить
определитель второго порядка
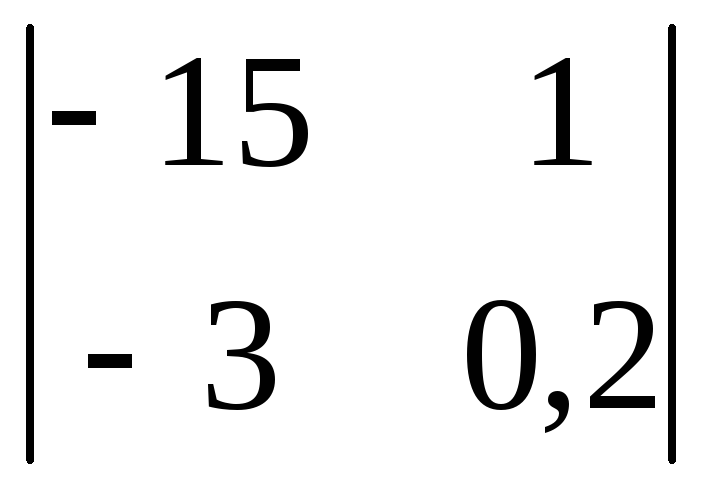 . .
-
Решить
систему:
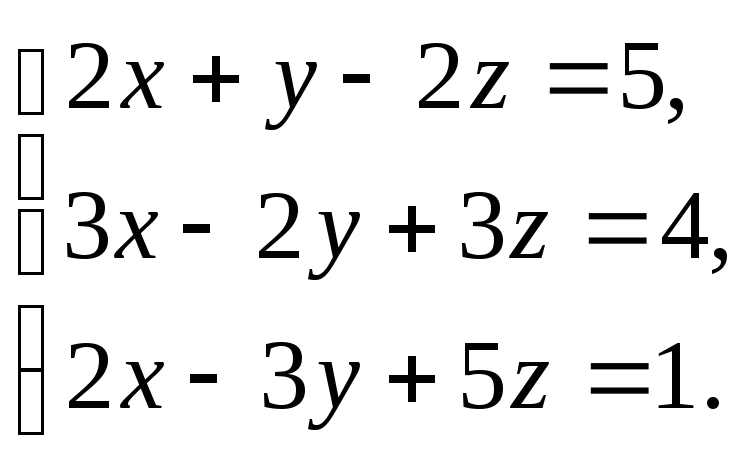
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
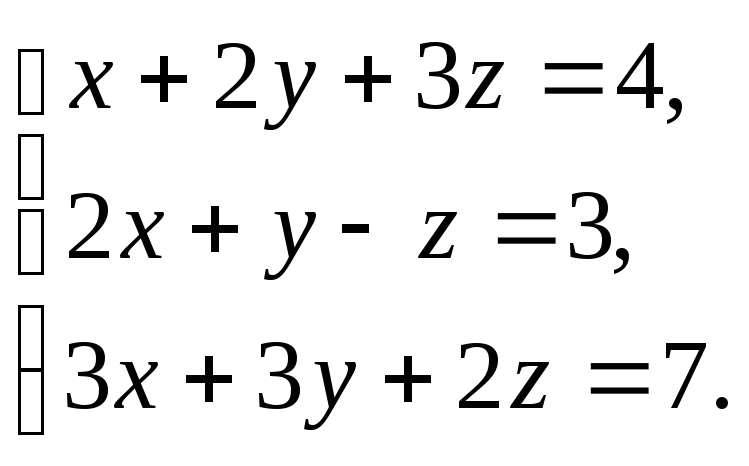
|
|
Вариант
14.
-
Найти
длины сторон треугольника с вершинами
А(2, 2, 2), В(4, 0, 3), С(0, 1, 0).
-
Дано:
вектор
 =2i–j–k,
вектор =2i–j–k,
вектор
 =i+j+4k.
Найти скалярное произведение векторов =i+j+4k.
Найти скалярное произведение векторов
 и и
 . .
-
Найти
произведение матриц АВ:
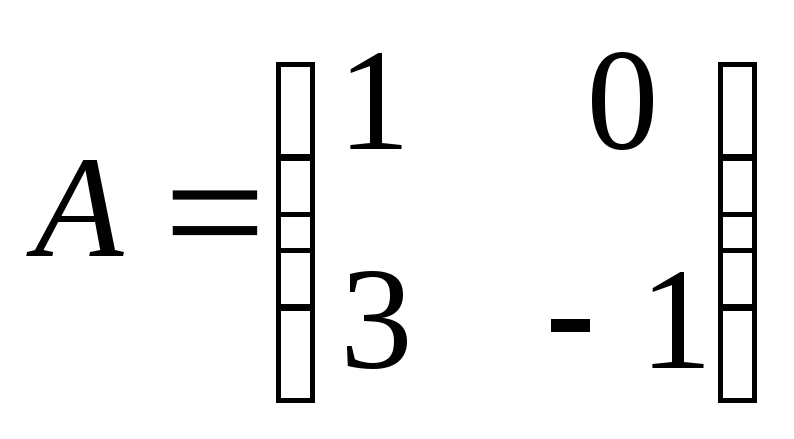 , ,
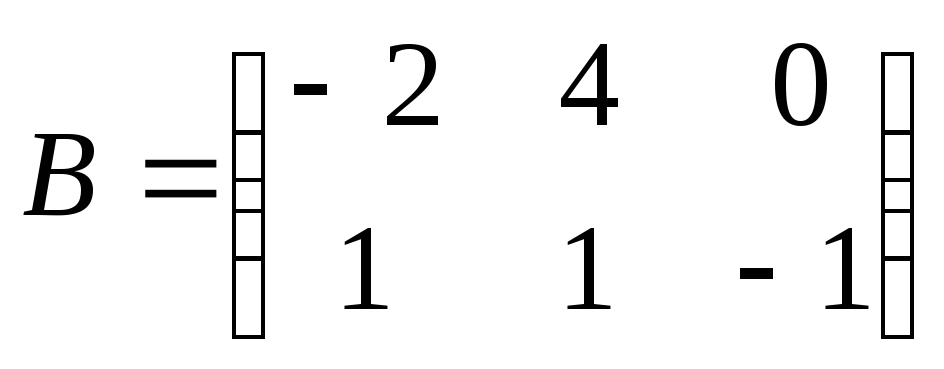 . .
-
Вычислить
определитель второго порядка
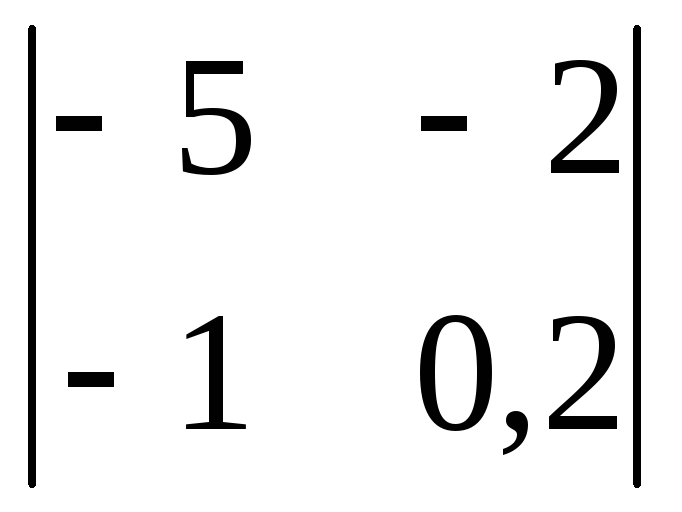 . .
-
Решить
систему:
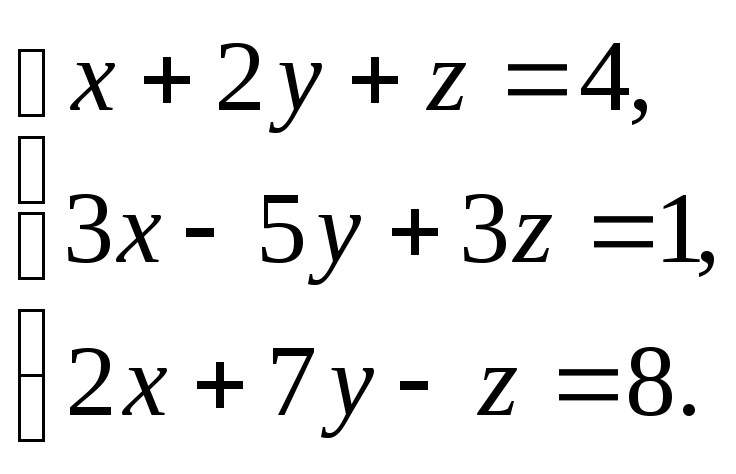
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
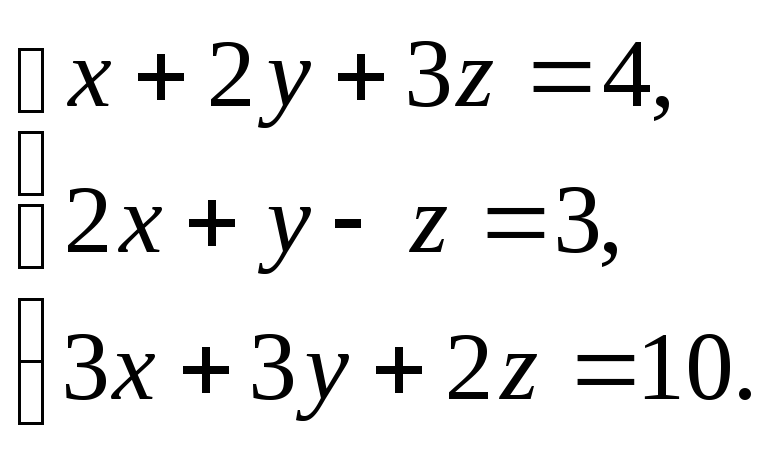
|
|
Вариант
15.
-
Найти
длину вектора
 + +
 ,
если ā=6i+3j–2k, ,
если ā=6i+3j–2k,
 =3i–2j+6k. =3i–2j+6k.
-
Дано:
т.А(2, 3, -1), т.В(4, 1, -2), т.С(1, 0, 2). Найти
проекцию вектора
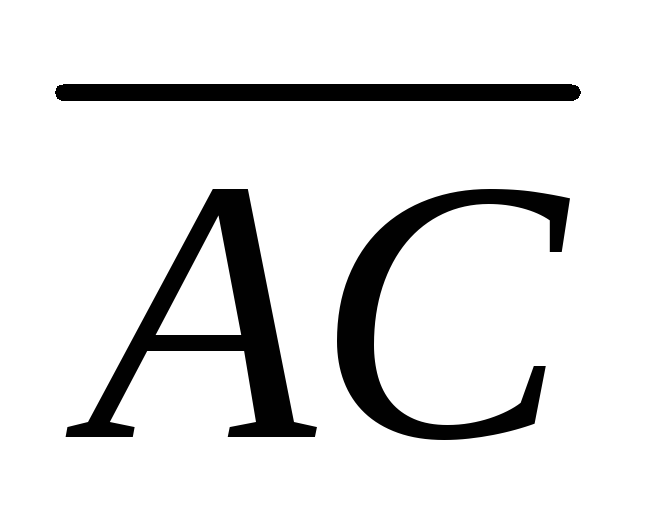 на вектор
на вектор
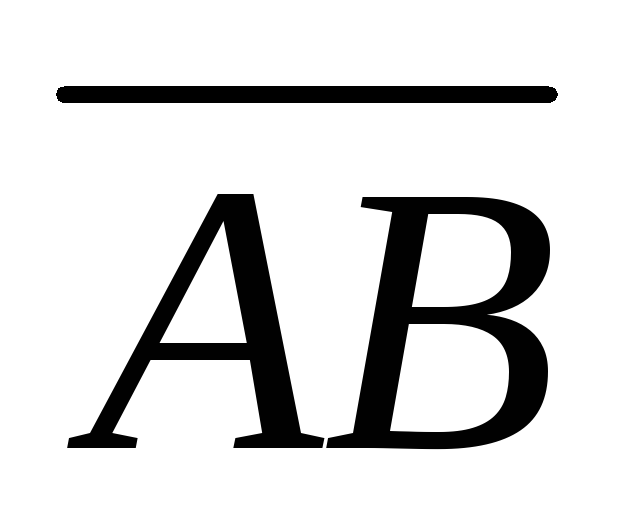 . .
-
Найти
произведение матриц ВА:
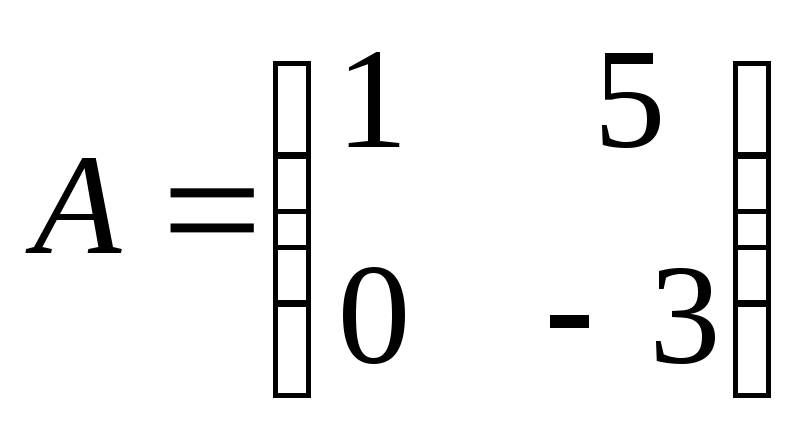 , ,
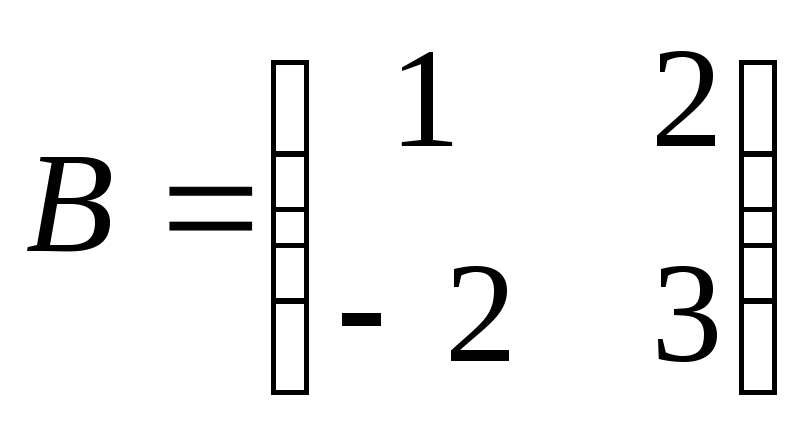 . .
-
Вычислить
определитель второго порядка
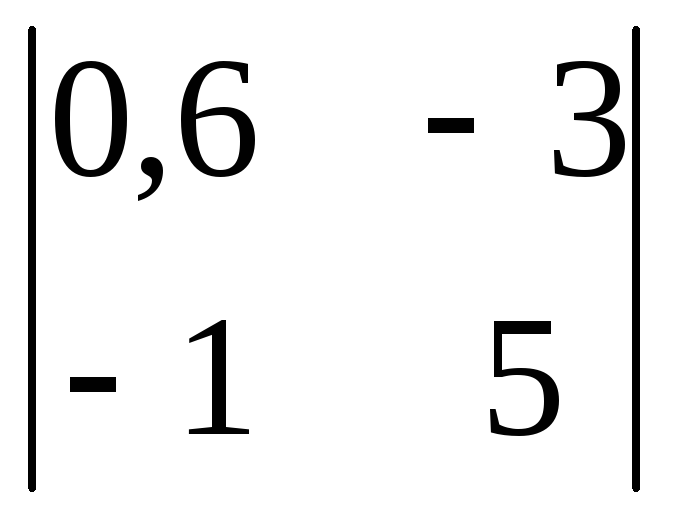 . .
-
Решить
систему:
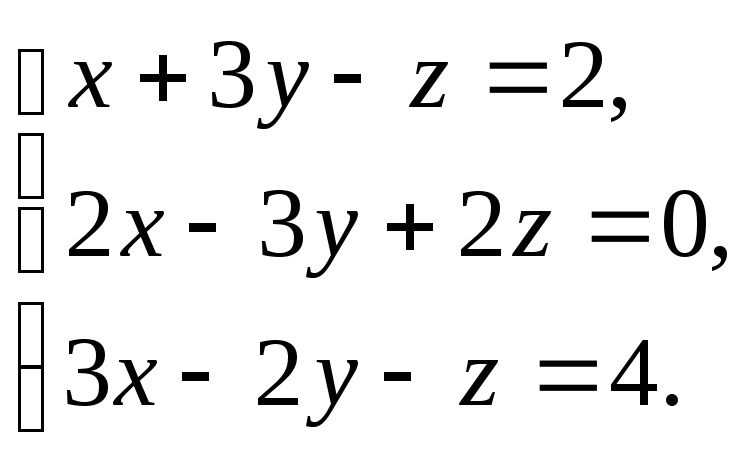
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
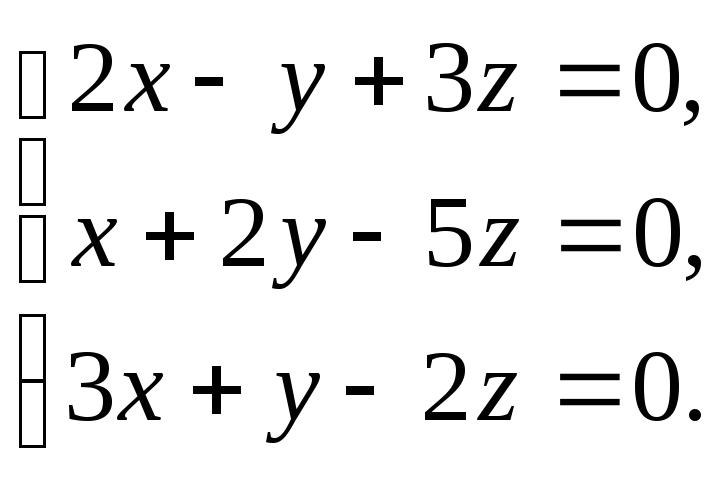
|
|
Вариант
16.
-
Дано:
т.А(5, 3, 7), т.В(3, 4, 1), т.С(-1, 2, 4), т.D(1,
2, 2). Найти вектор
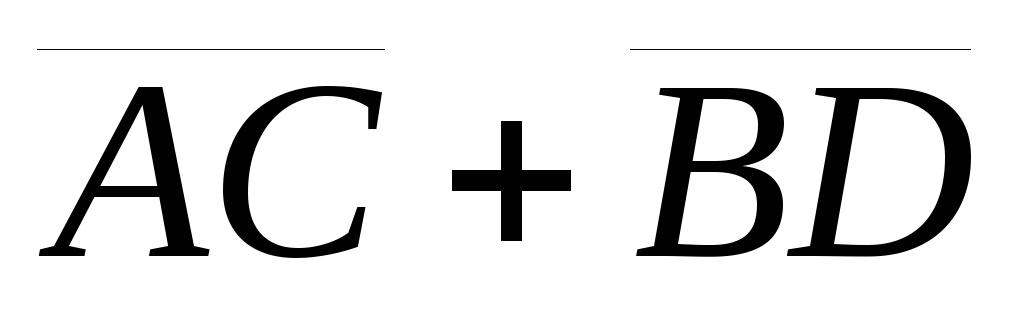 .
.
-
Дано:
вектор
 =3i+4j+5k, =3i+4j+5k,
 =4i+5j–3k.
Найти угол между векторами =4i+5j–3k.
Найти угол между векторами
 и и
 . .
-
Найти
произведение матриц ВА:
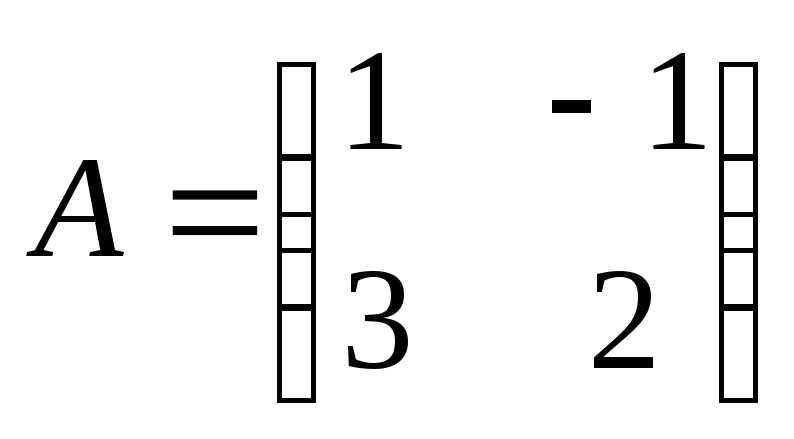 , ,
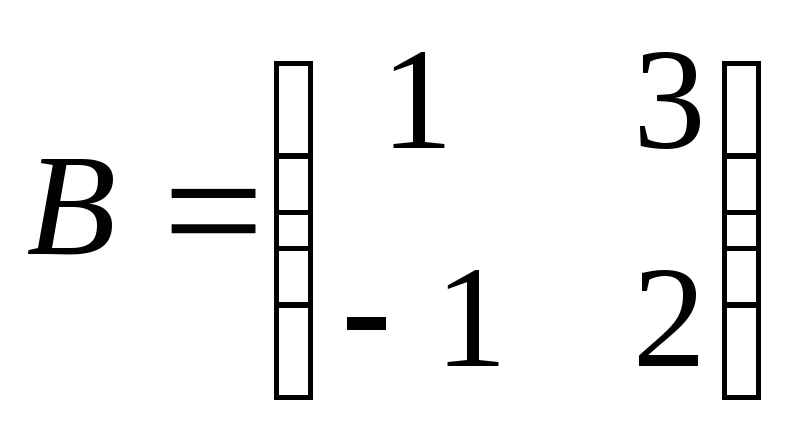 . .
-
Вычислить
определитель второго порядка
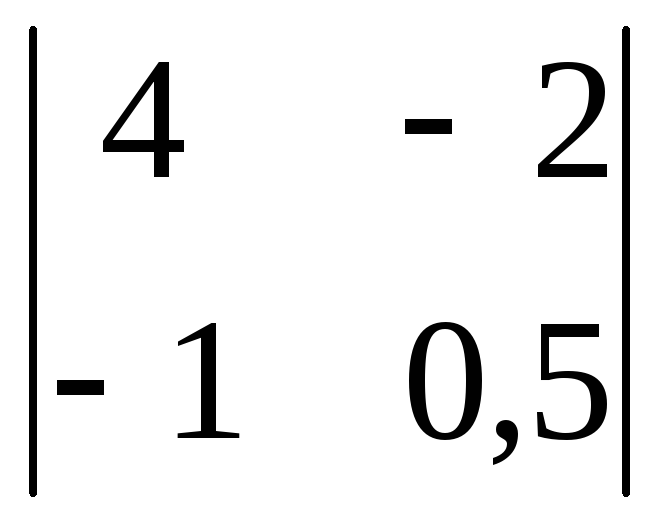 . .
-
Решить
систему:
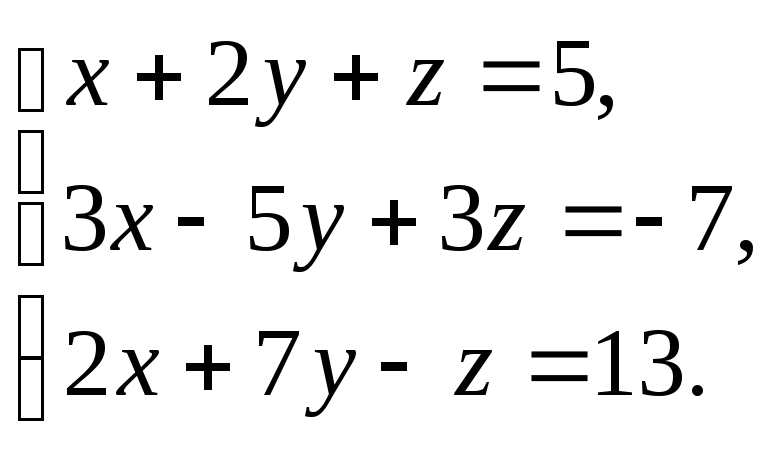
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений

|
|
Вариант
17.
-
Найти
длину вектора 2 – – ,
если ,
если
 =3i+4j+5k, =3i+4j+5k,
 =4i+5j–3k. =4i+5j–3k.
-
Дан
треугольник с вершинами А(1, 1, -1), В(2,
3, 1), С(3, 2, 1). Найти угол при вершине В.
-
Найти
произведение матриц АВ:
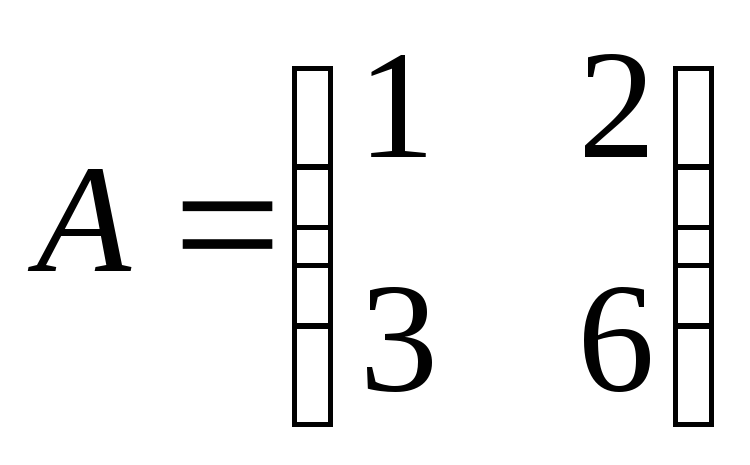 , ,
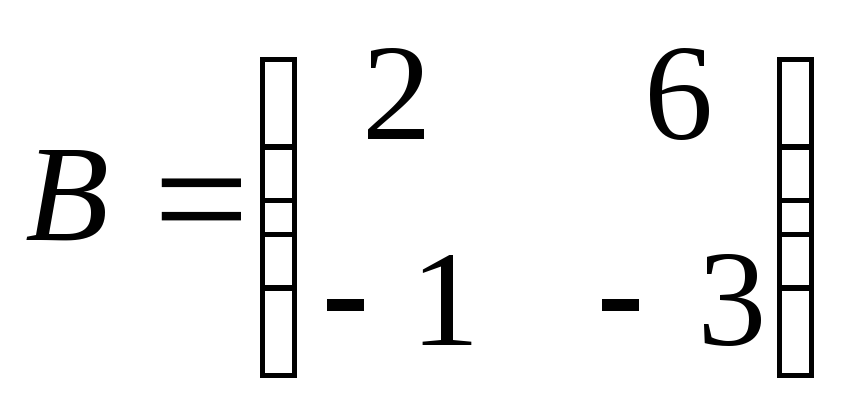 . .
-
Вычислить
определитель второго порядка
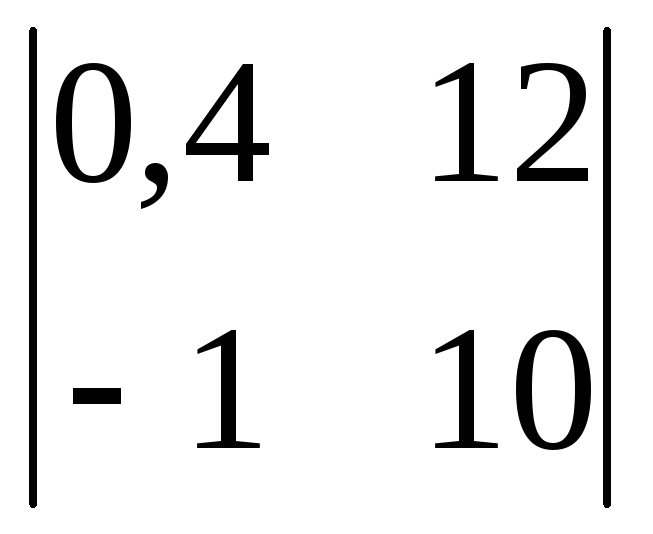 . .
-
Решить
систему:
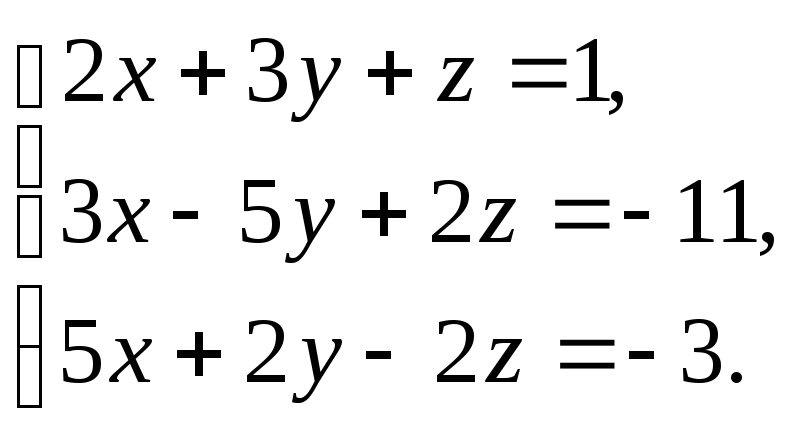
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений

|
|
Вариант
18.
-
Найти
длину вектора ā=2i+3j+5k и его направление.
-
Найти
скалярное произведение (3 –2 –2 ,
5 ,
5 –6 –6 ),
если модуль вектора ),
если модуль вектора
 равен 4, модуль вектора
равен 4, модуль вектора
 равен 6, угол между векторами
равен 6, угол между векторами
 и и
 равен 60º.
равен 60º.
-
Найти
произведение матриц АВ:
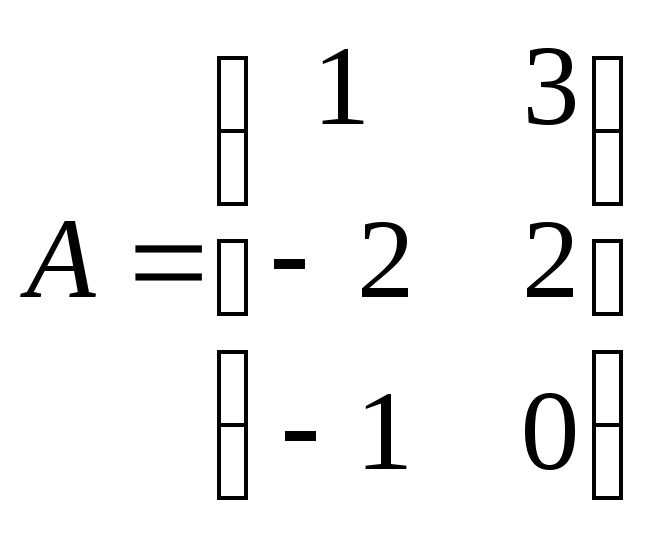 , ,
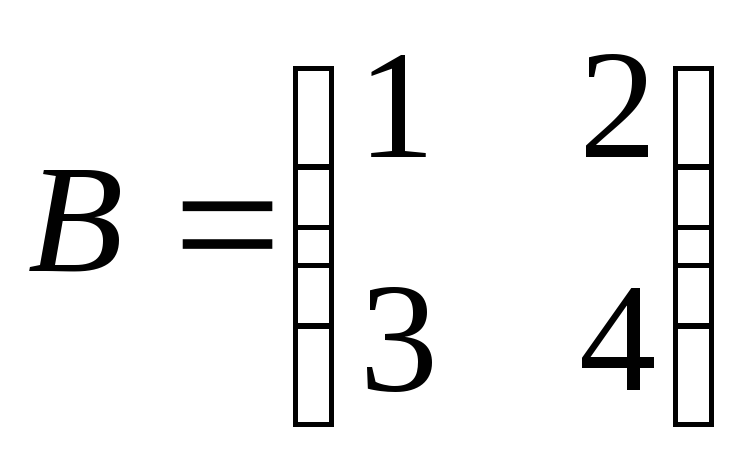 . .
-
Вычислить
определитель второго порядка
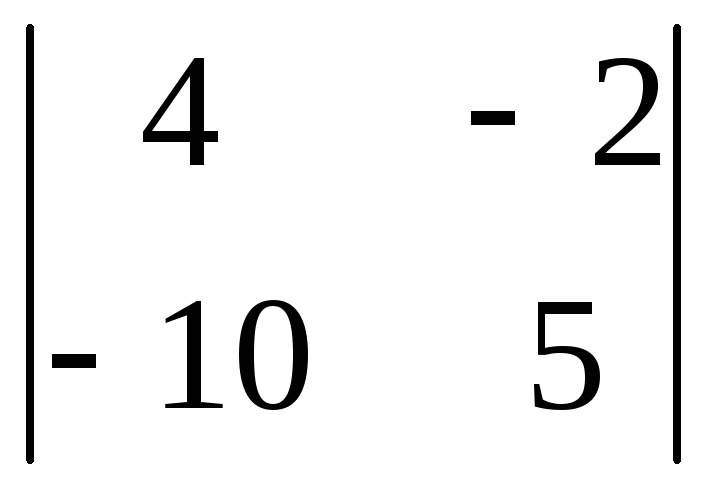 . .
-
Решить
систему:
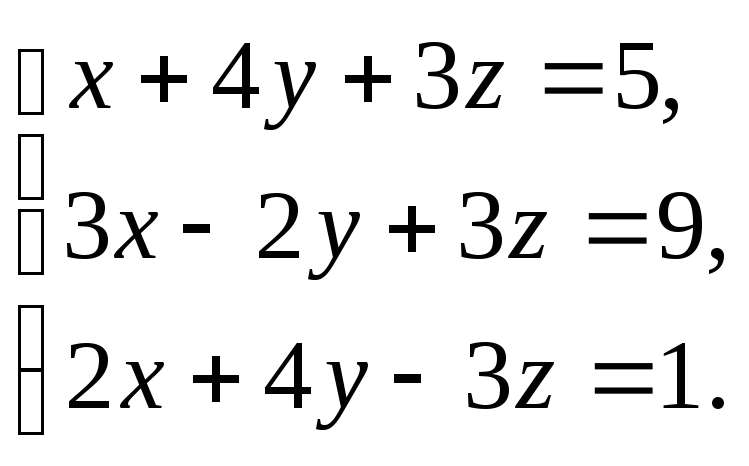
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений

|
|
Вариант
19.
-
Найти
длины сторон треугольника с вершинами
А(0, 0, 1), В(2, 3, 5), С(6, 2, 3).
-
Найти
скалярное произведение векторов
ā=6i+3j–2k и
 =3i–2j+6k. =3i–2j+6k.
-
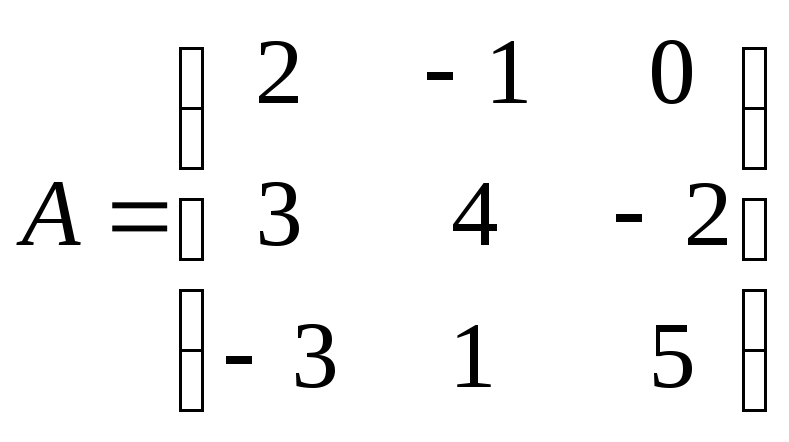
Найти
произведение матриц ВА:
 , ,
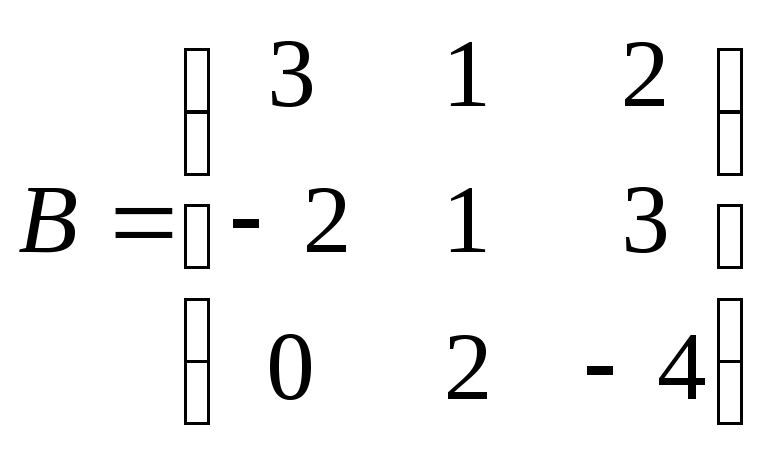 . .
-
Вычислить
определитель второго порядка
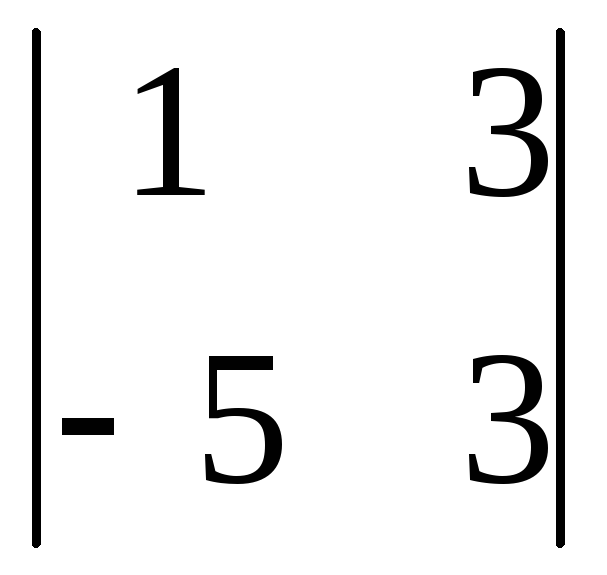 . .
-
Решить
систему:
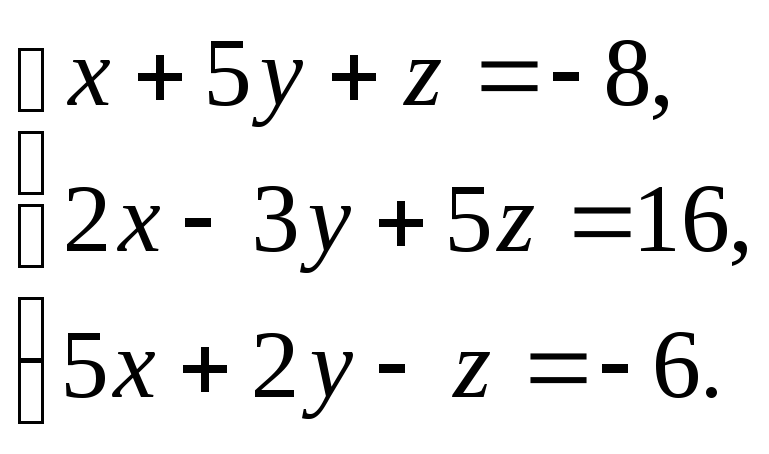
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
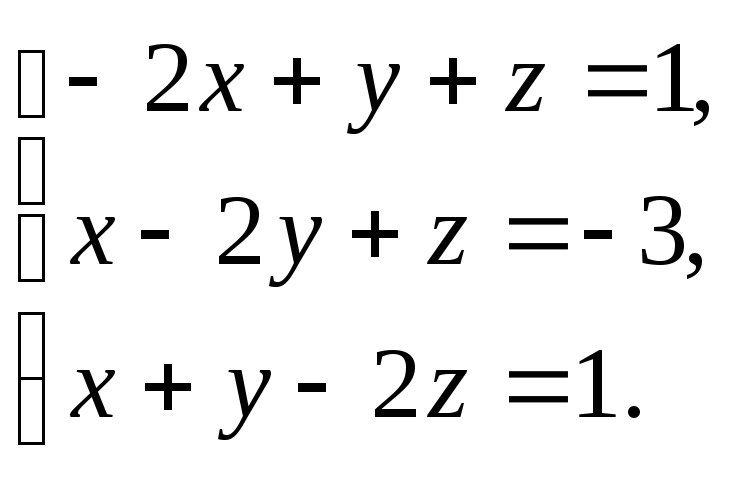
|
|
Вариант
20.
-
Найти
длину вектора
 + +
 ,
если ā=6i+3j–2k, ,
если ā=6i+3j–2k,
 =3–2j+6k. =3–2j+6k.
-
Дан
треугольник с вершинами А(0, 0, 1), В(2,
3, 5), С(6, 2, 3). Найти угол при вершине В.
-
Найти
произведение матриц ВА:
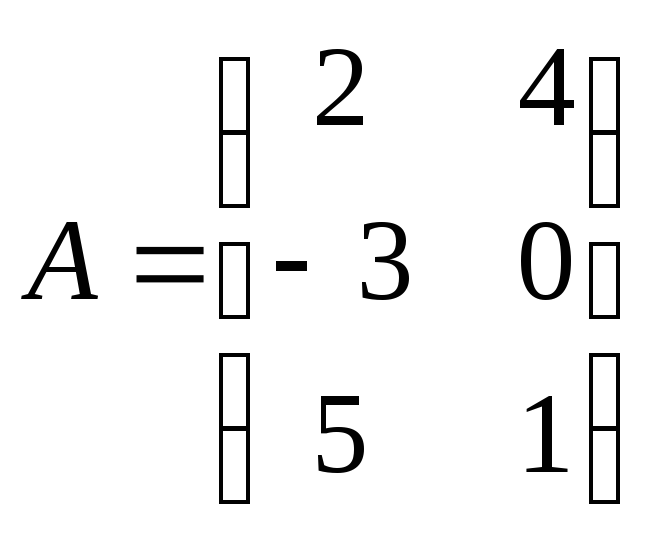 , ,
 . .
-
Вычислить
определитель второго порядка
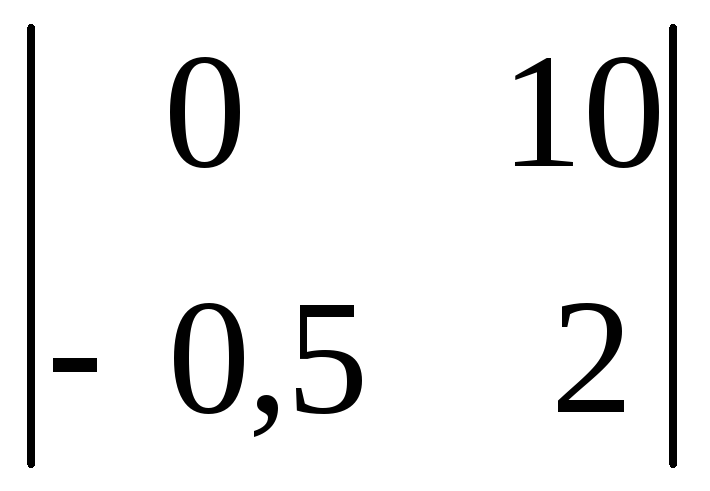 . .
-
Решить
систему:

-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
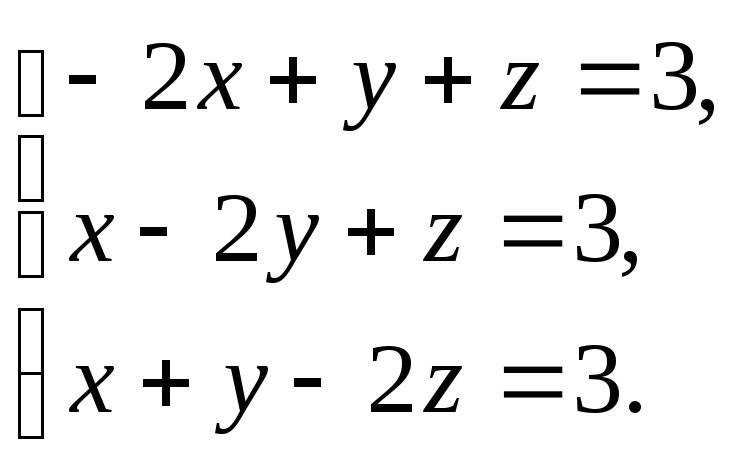
|
|
Вариант
21.
-
Дано:
т.А(5, 7, -2), т.В(3, 1, 1), т.С(9, 4, 4), т.Д(1, 5, 0).
Найти вектор
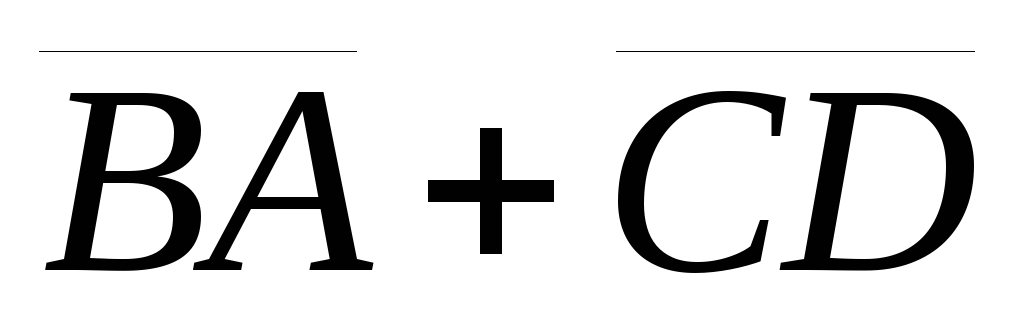 . .
-
Дано:
вектор
 =2i–j–6k,
вектор =2i–j–6k,
вектор
 =i–2j+4k.
Найти проекцию вектора =i–2j+4k.
Найти проекцию вектора
 на вектор
на вектор
 . .
-
Найти
произведение матриц АВ:
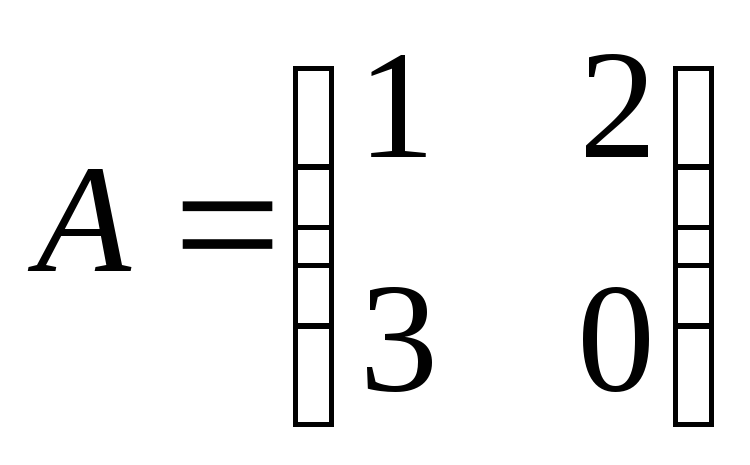 , ,
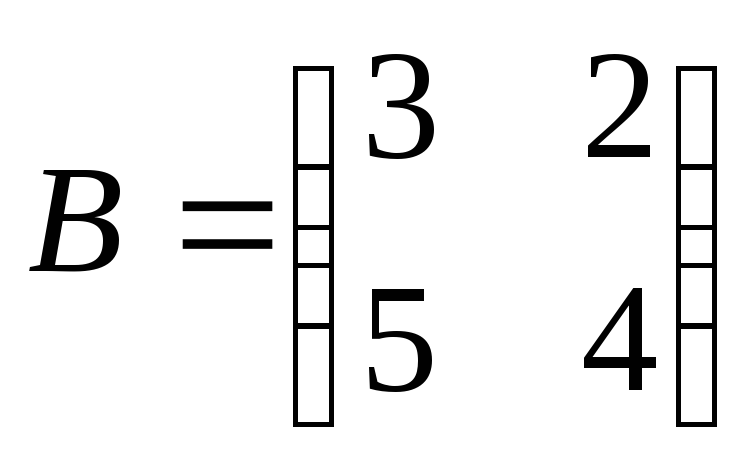 . .
-
Вычислить
определитель второго порядка
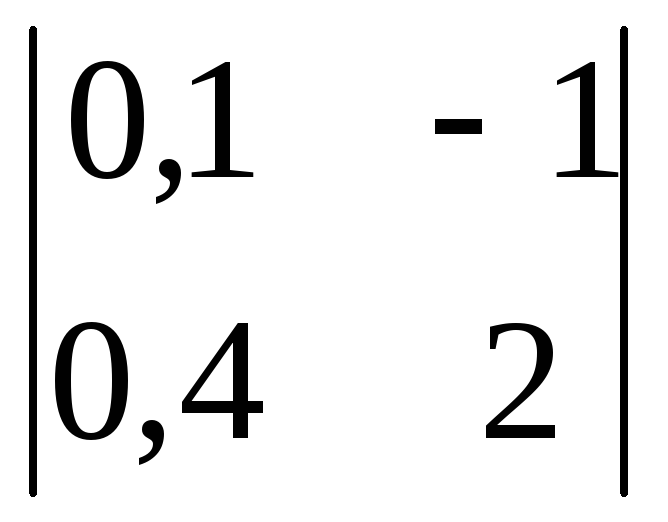 . .
-
Решить
систему:
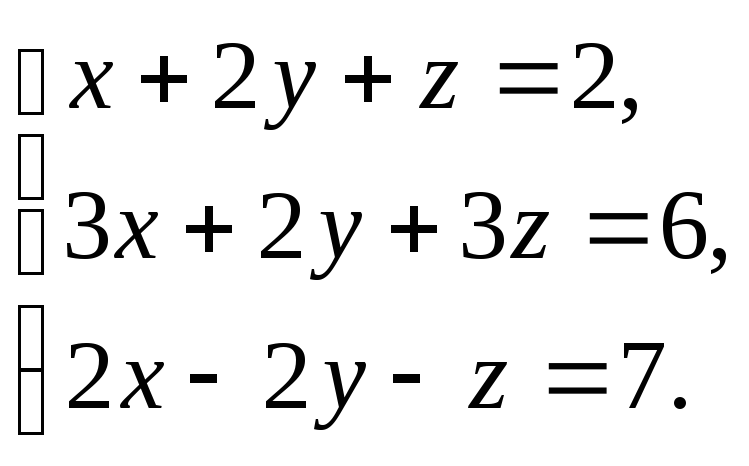
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
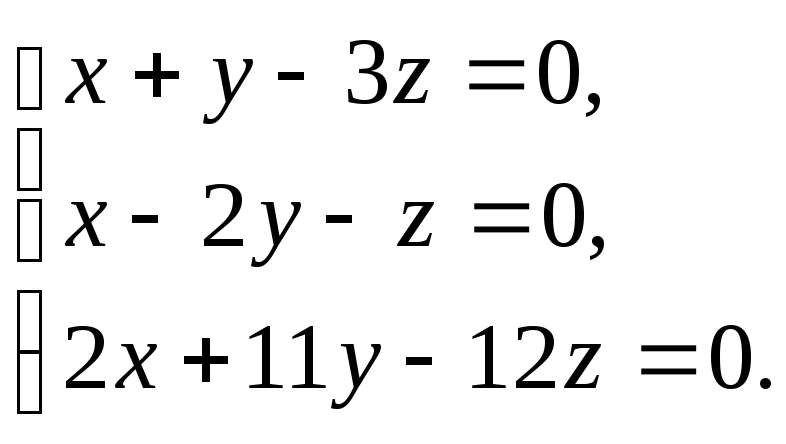
|
|
Вариант
22.
-
Найти
длину вектора ā= –i+5j–6k и его направление.
-
Дано:
модуль вектора
 равен 5, модуль вектора
равен 5, модуль вектора
 равен 4, угол между векторами
равен 4, угол между векторами
 и и
 равен 45º. Найти модуль вектора
равен 45º. Найти модуль вектора
 =2 =2 – – . .
-
Найти
произведение матриц ВА:
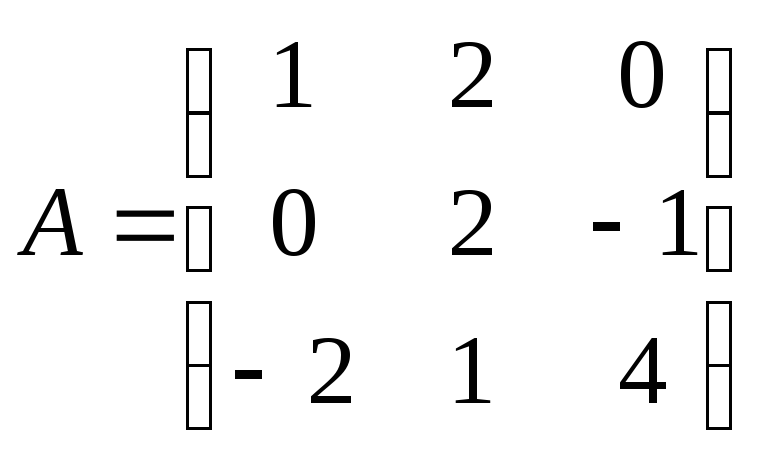 , ,
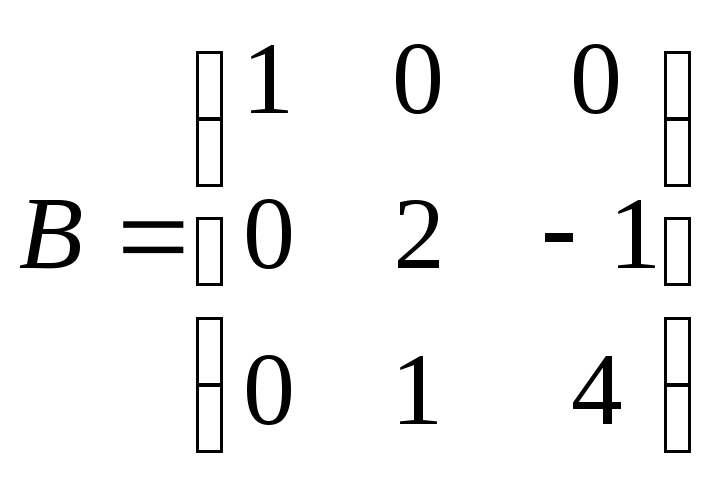 . .
-
Вычислить
определитель второго порядка
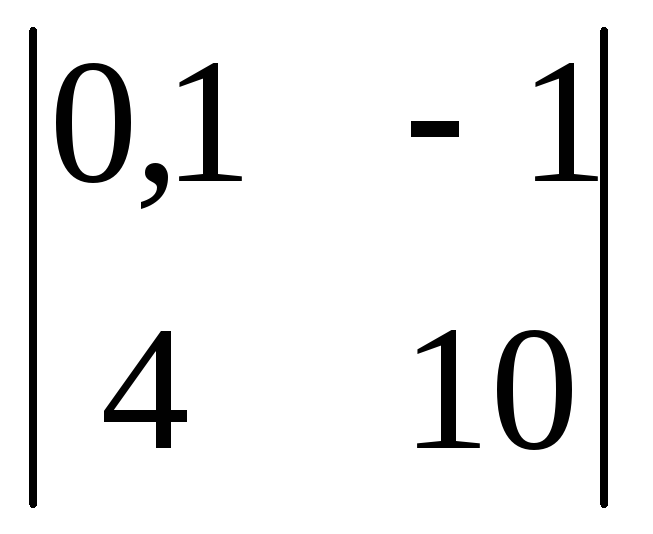 . .
-
Решить
систему:
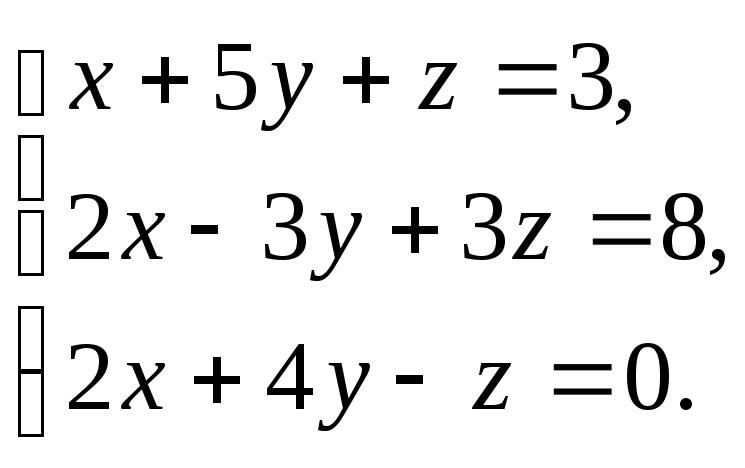
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
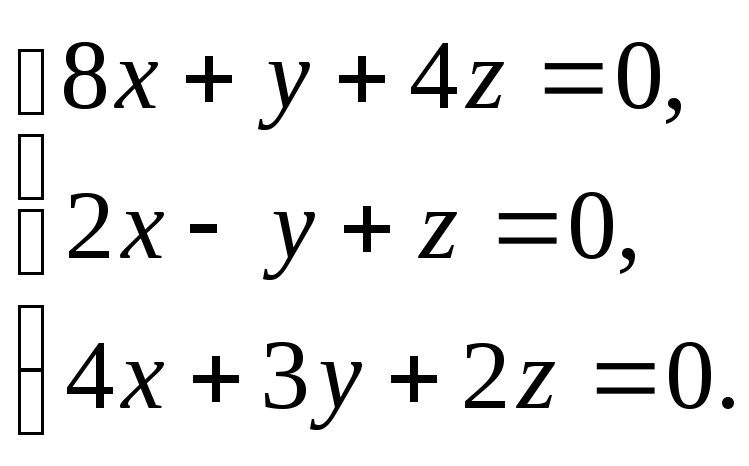
|
|
Вариант
23.
-
Дано:
т.А(0, 6, 2), т.В(-3, 4, 2). Найти длину вектора
 и направление.
и направление.
-
Дано:
вектор
 =
–i+3j+4k, вектор =
–i+3j+4k, вектор
 =2i–j+2k.
Найти проекцию вектора =2i–j+2k.
Найти проекцию вектора
 на вектор
на вектор
 . .
-
Найти
произведение матриц ВА:
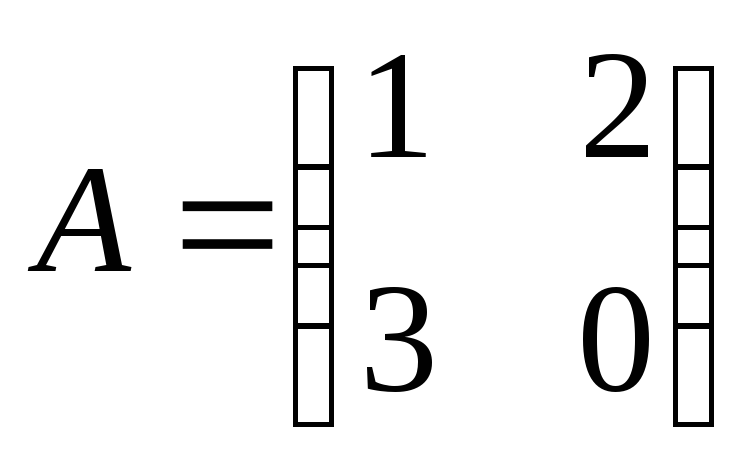 , ,
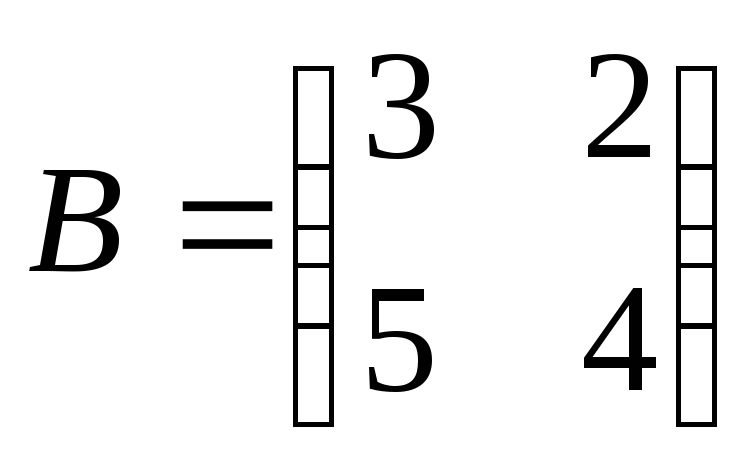 . .
-
Вычислить
определитель второго порядка
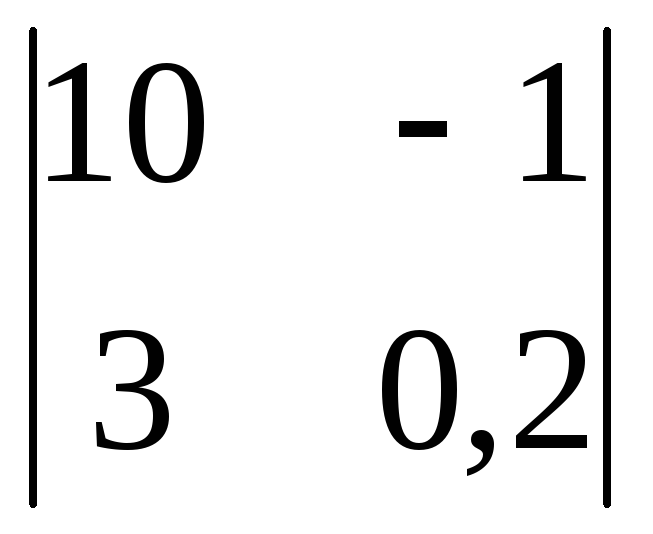 . .
-
Решить
систему:
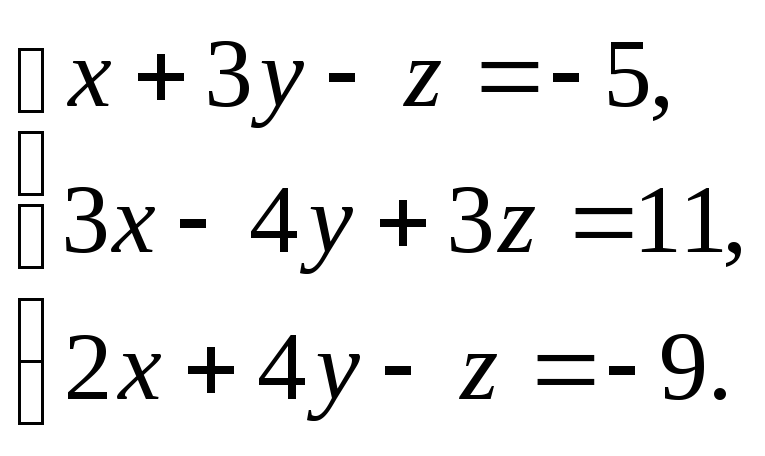
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
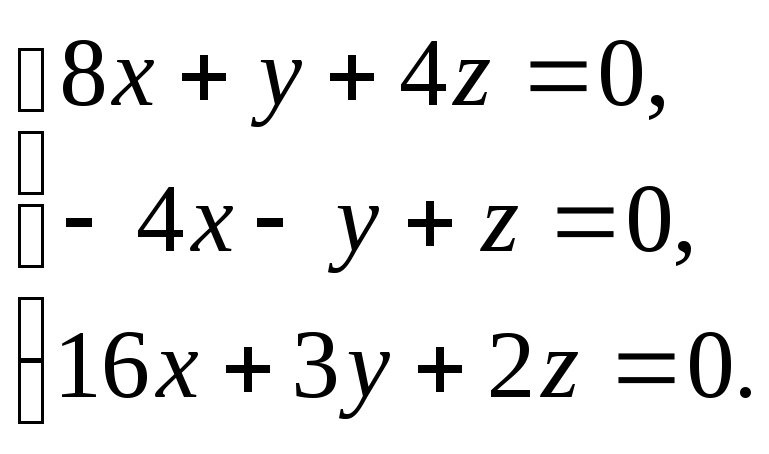
|
|
Вариант
24.
-
Дано:
вектор
 =–2i+3j–2k,
вектор =–2i+3j–2k,
вектор
 =2i+k.
Найти длину вектора =2i+k.
Найти длину вектора
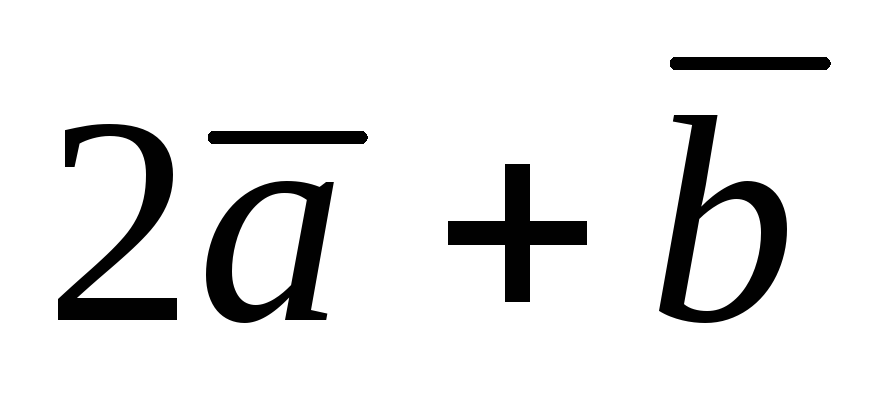 . .
-
Дан
треугольник с вершинами А(0, 3, 1), В(2,
0, 5), С(1, 2, 3). Найти угол при вершине A.
-
Найти
произведение матриц АВ:
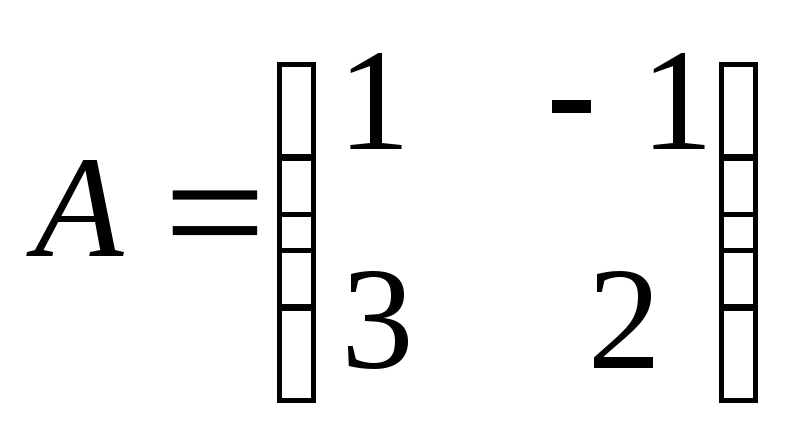 , ,
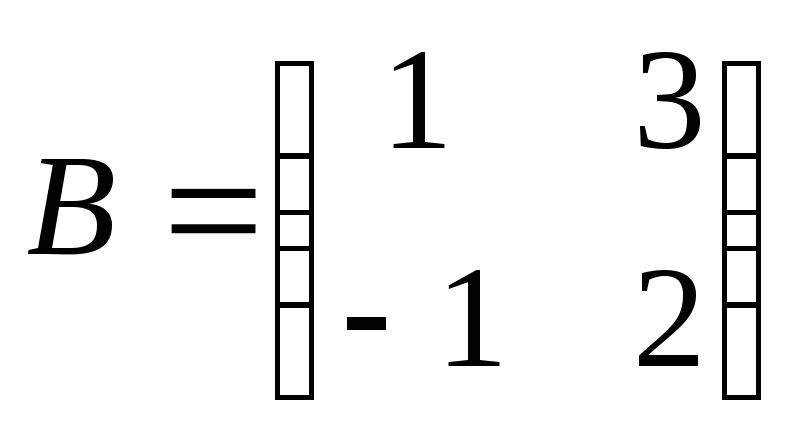 . .
-
Вычислить
определитель второго порядка
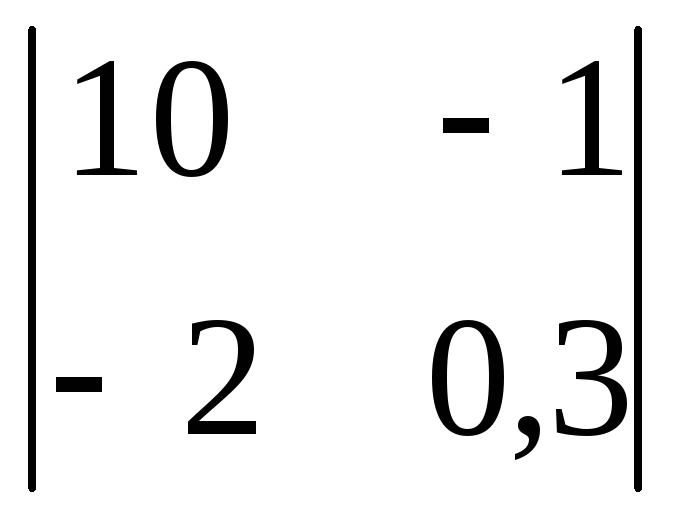 . .
-
Решить
систему:
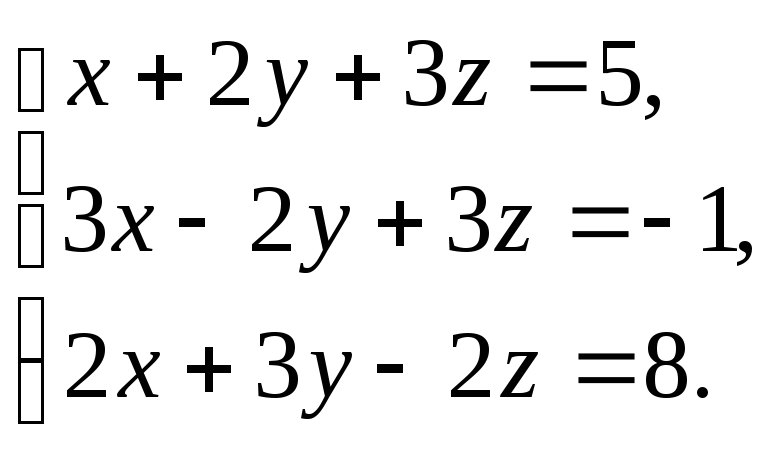
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
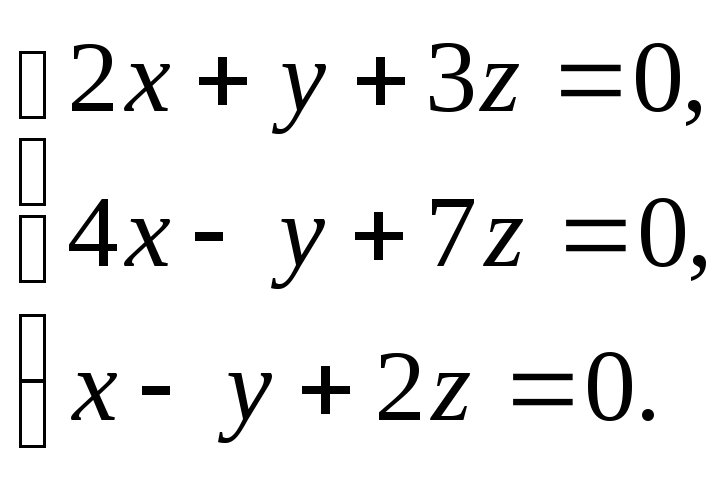
|
|
Вариант
25.
-
Дано:
вектор
 =–i+j,
вектор =–i+j,
вектор
 =2i+j+4k.
Найти длину вектора =2i+j+4k.
Найти длину вектора
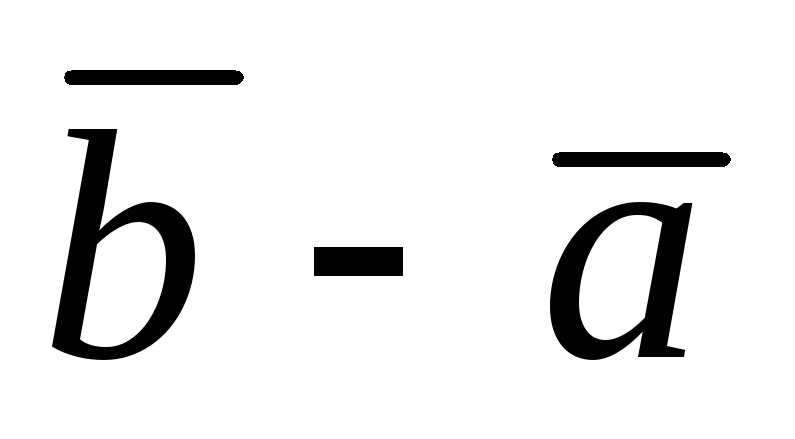 . .
-
Дано:
т.А(3, 3, 1), т.В(0, 1, -2), т.С(-1, 3, 2). Найти
проекцию вектора
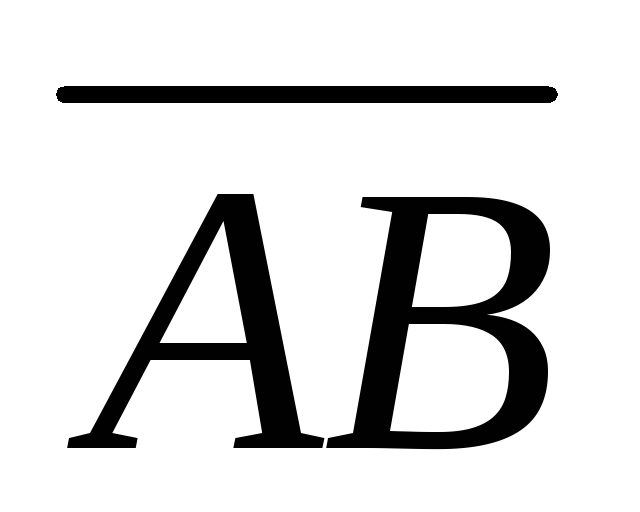 на вектор
на вектор
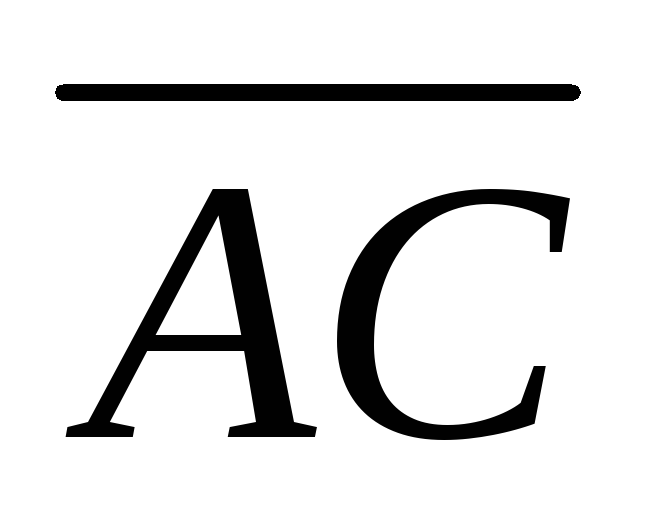 . .
-
Найти
произведение матриц АВ:
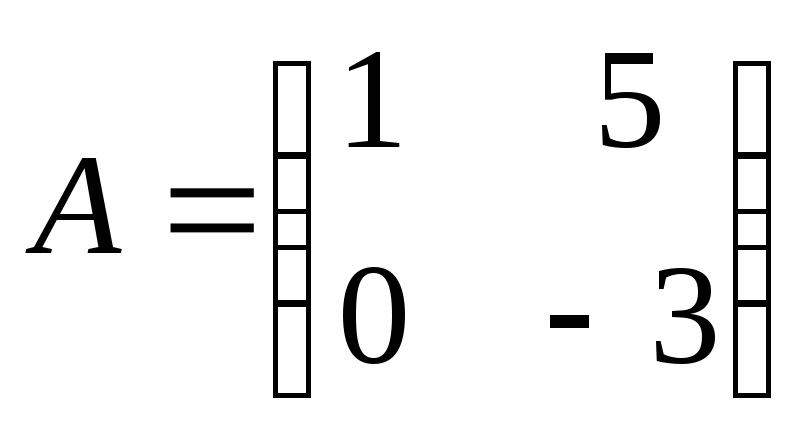 , ,
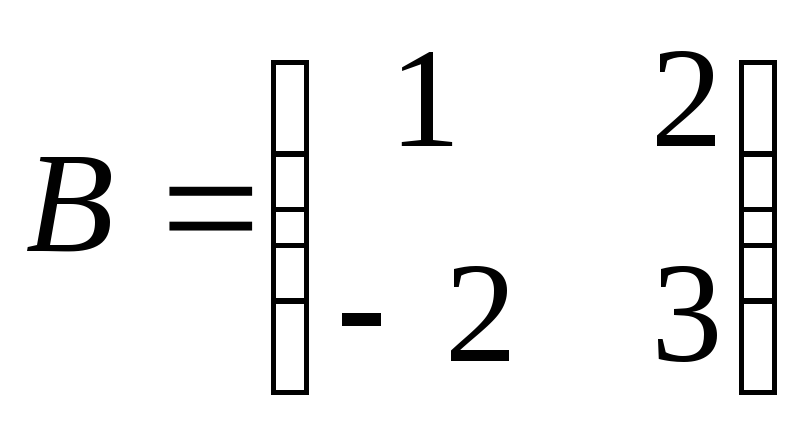 . .
-
Вычислить
определитель второго порядка
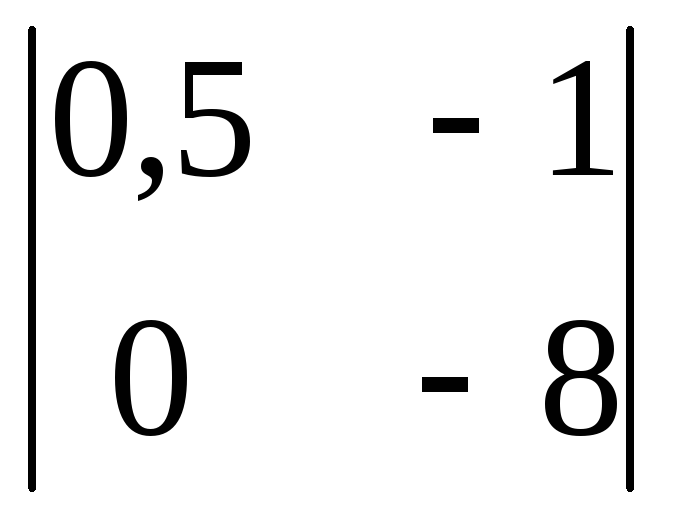 . .
-
Решить
систему:
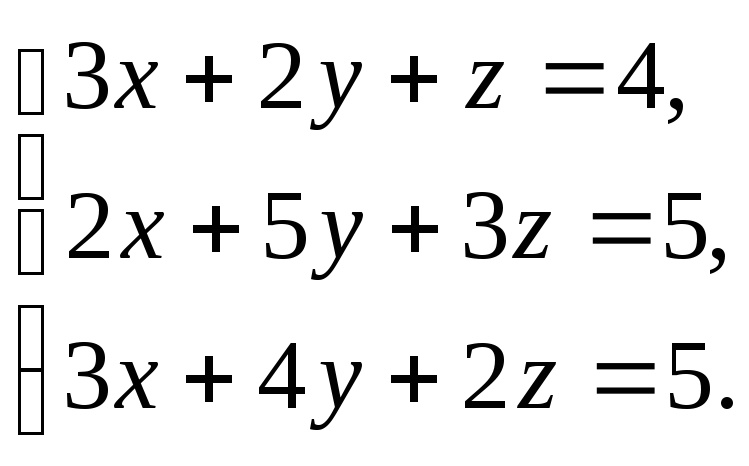
-
с
помощью обратной матрицы;
-
по
формулам Крамера;
-
методом
Гаусса.
-
Решить
систему уравнений
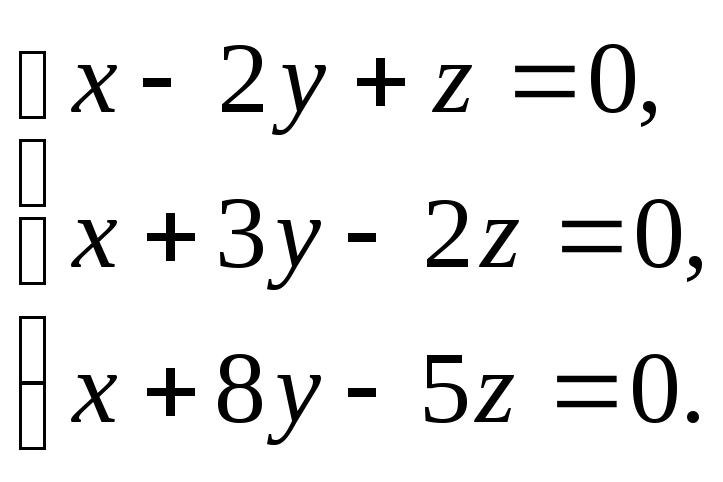
|


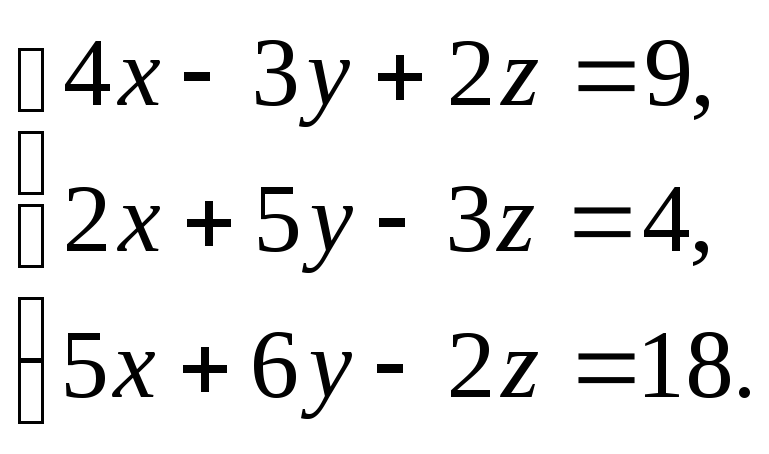
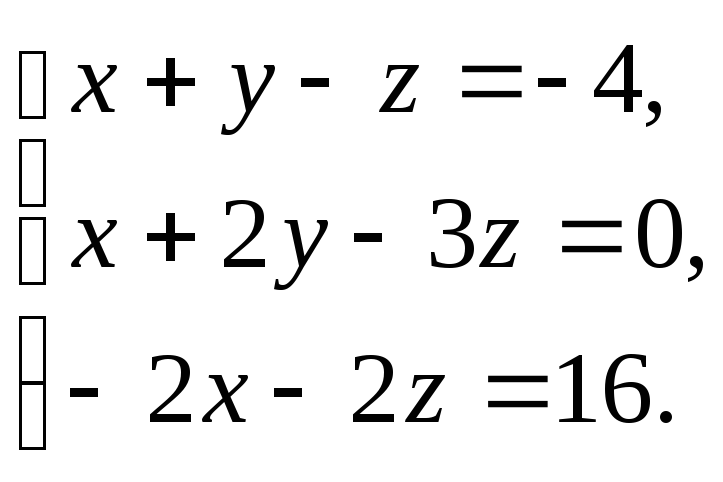
 ,
,
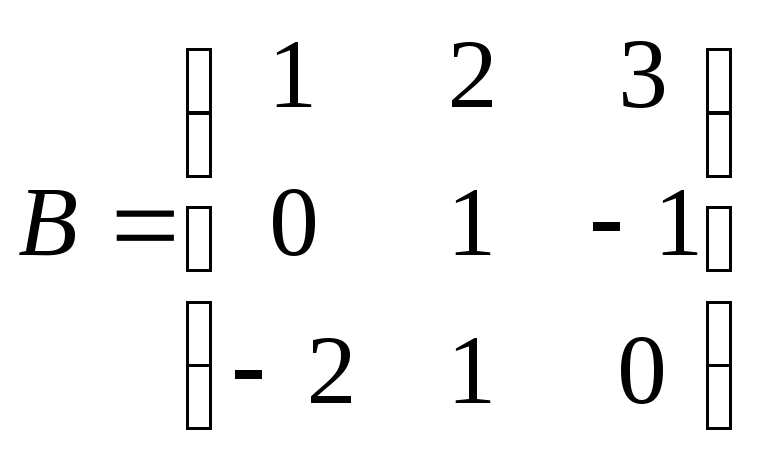 .
.
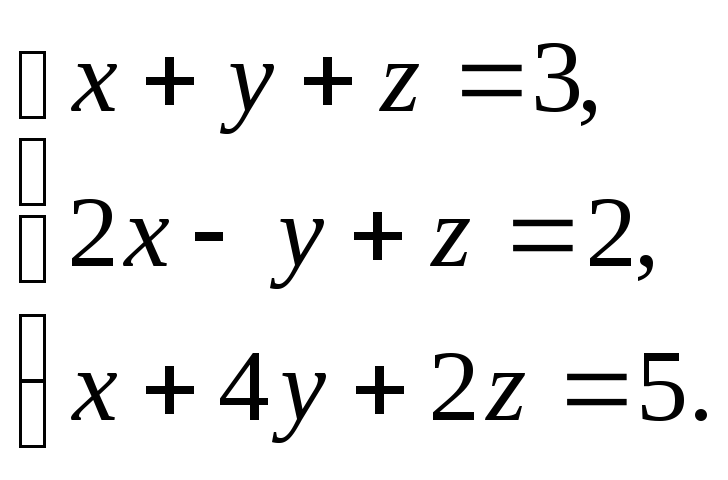
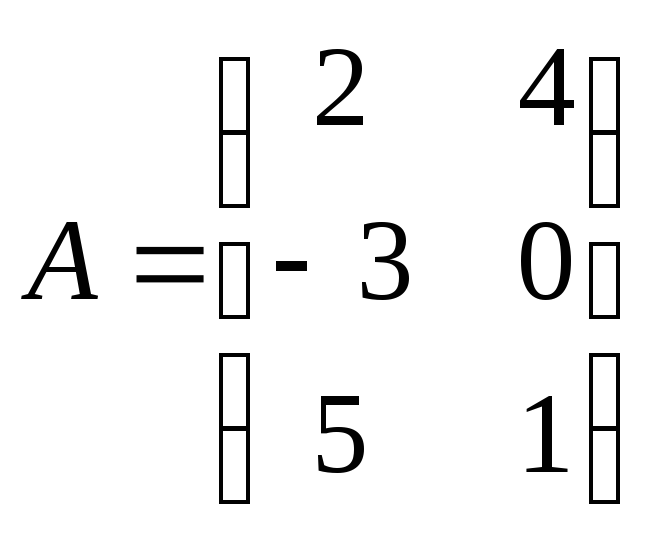 ,
,
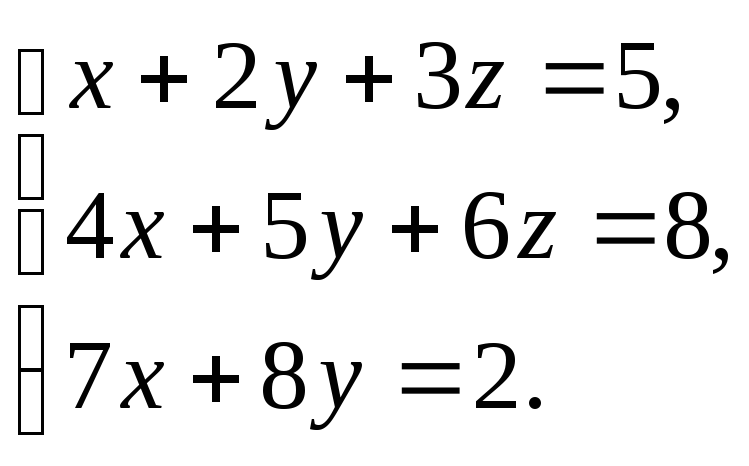
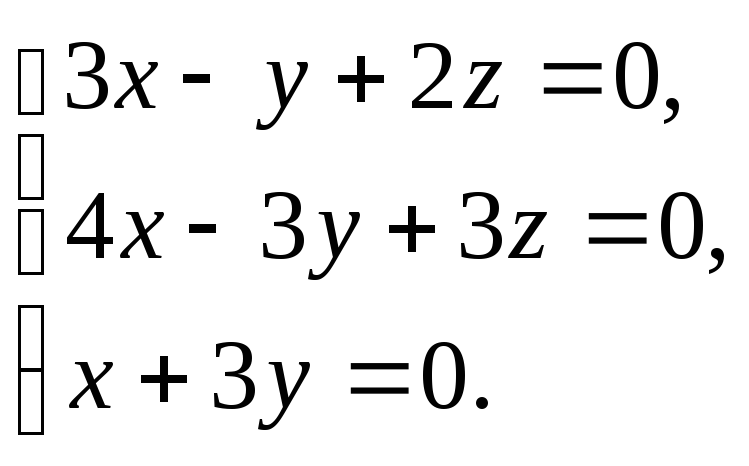
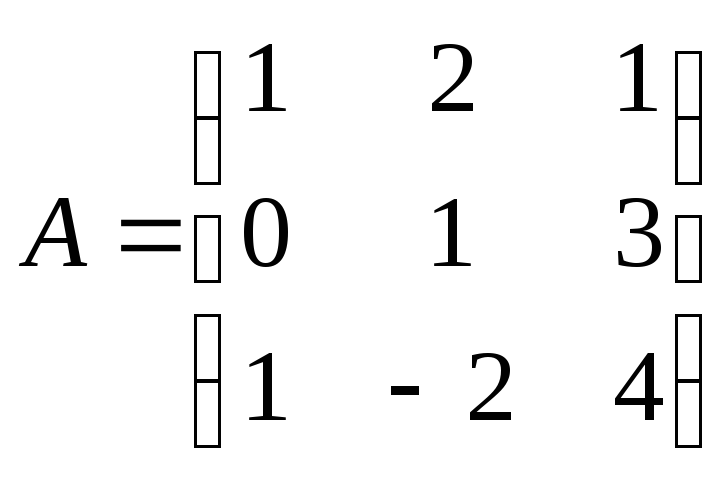 ,
,
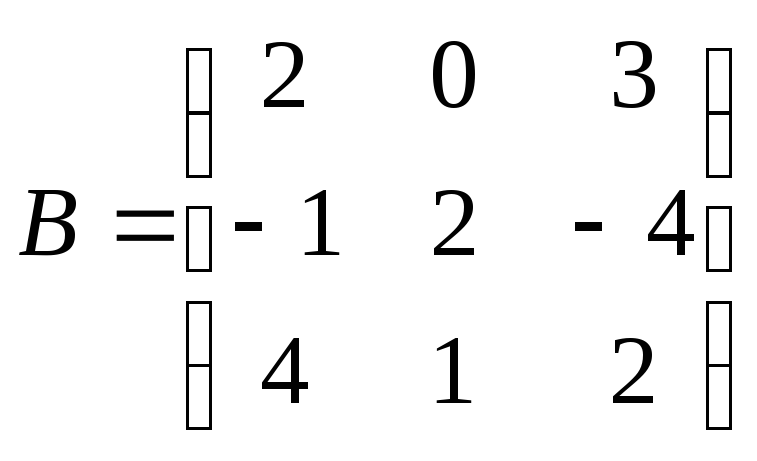 .
.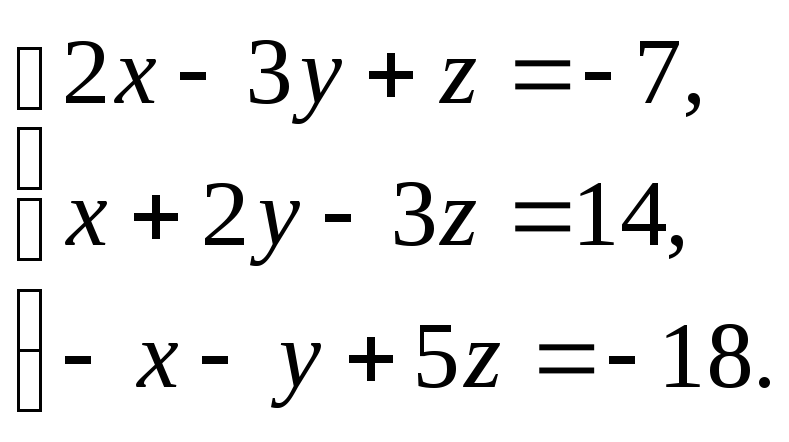
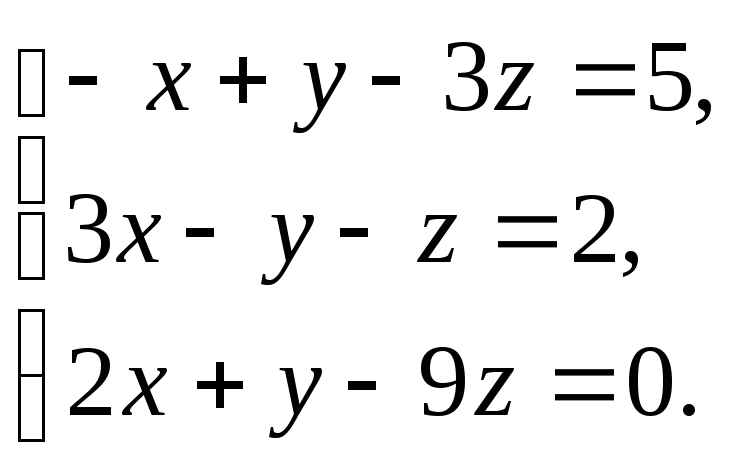
 ,
,
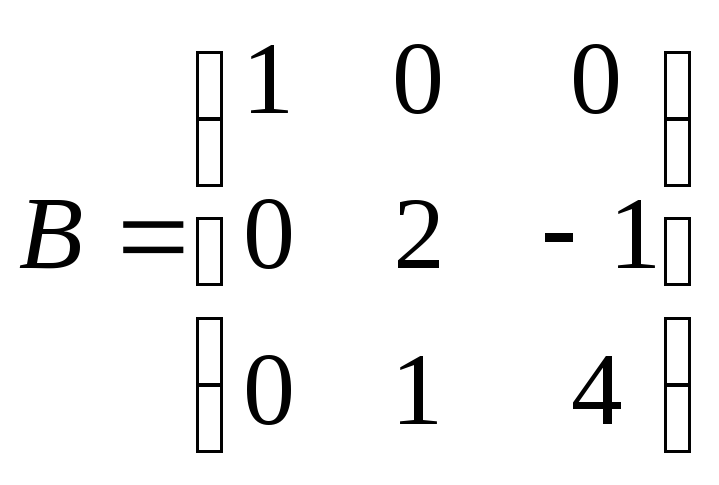 .
.
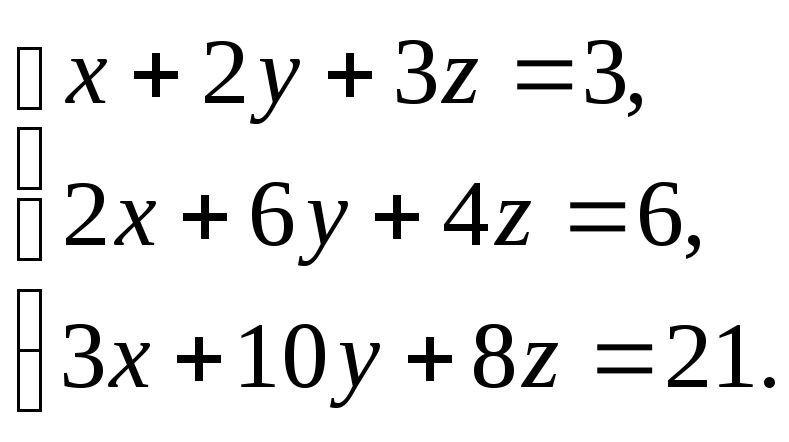
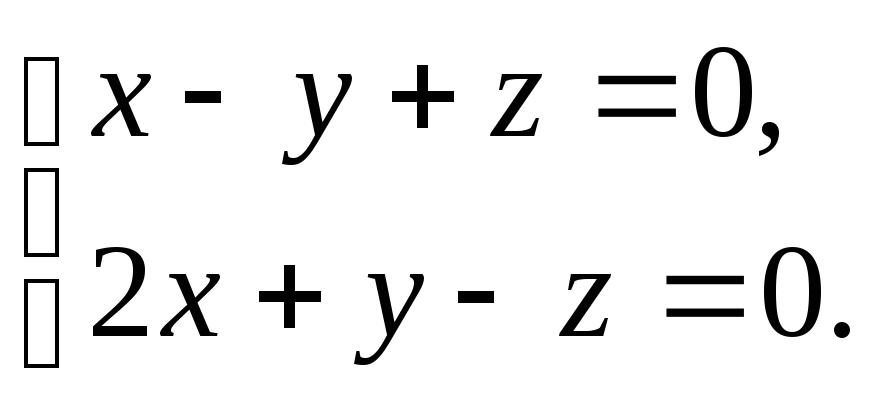
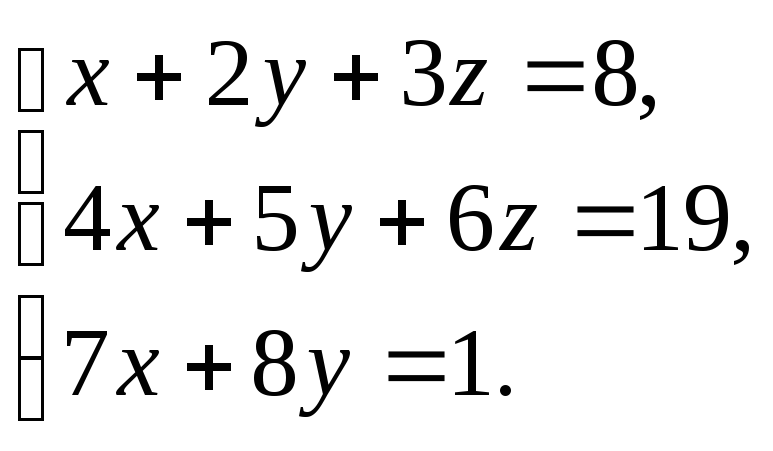
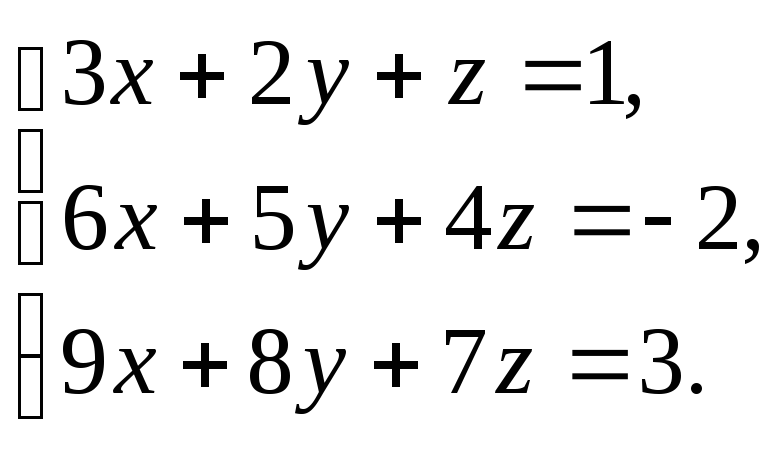
 ,
,
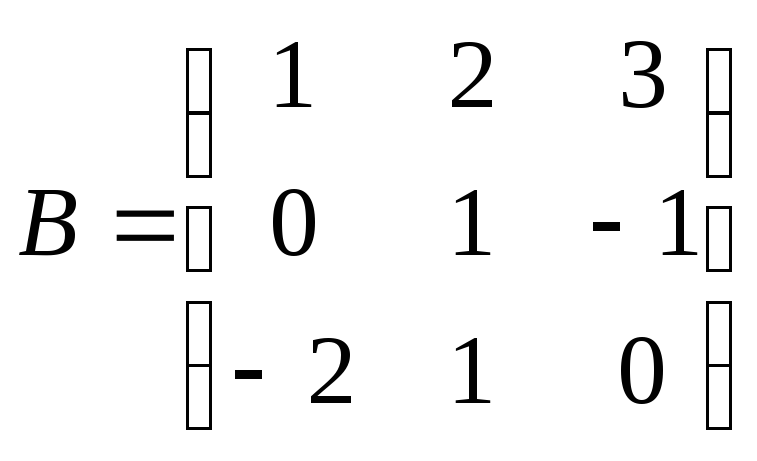 .
.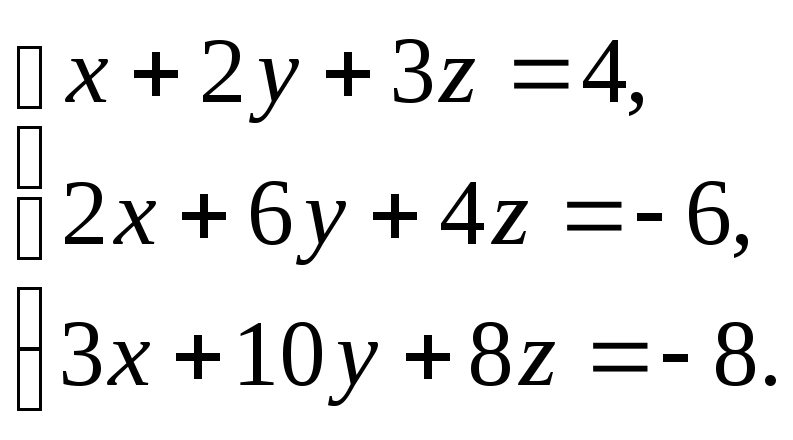
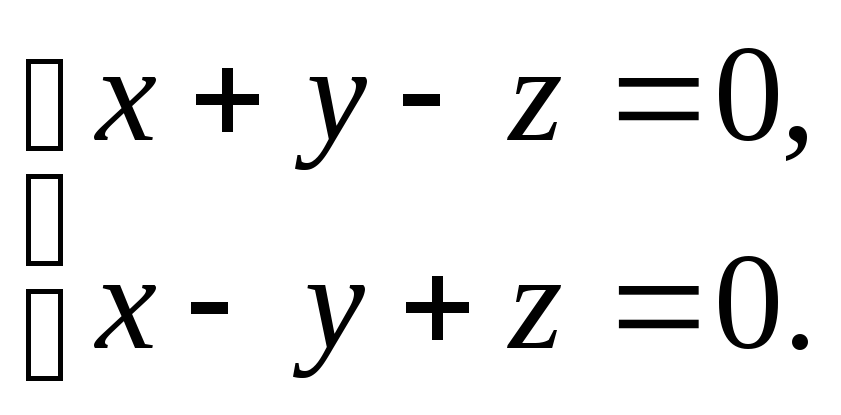
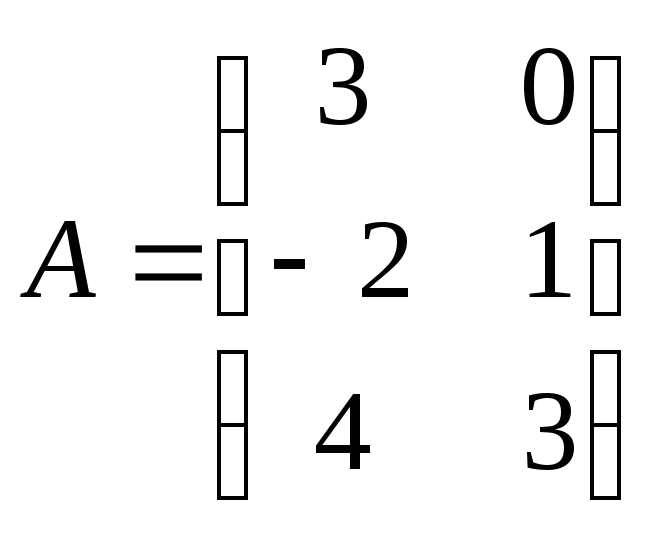 ,
,
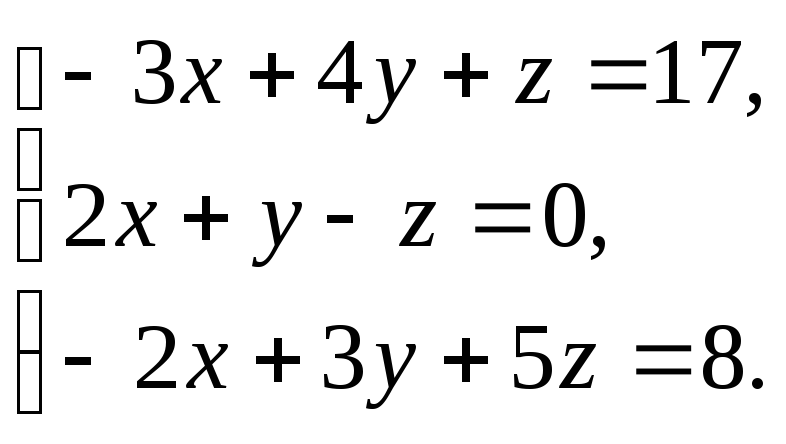
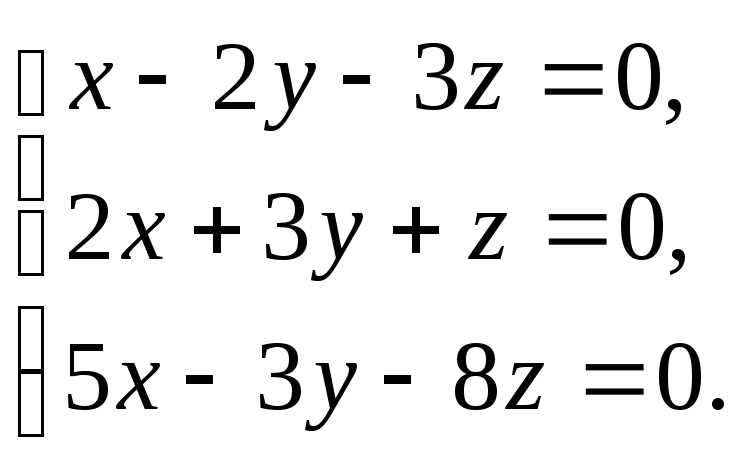
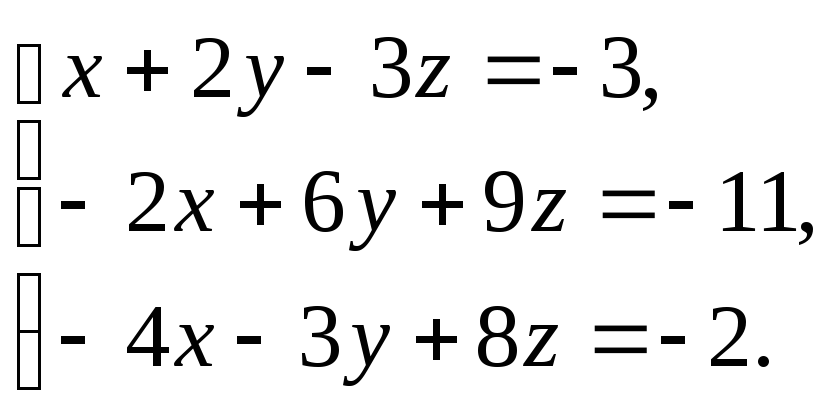
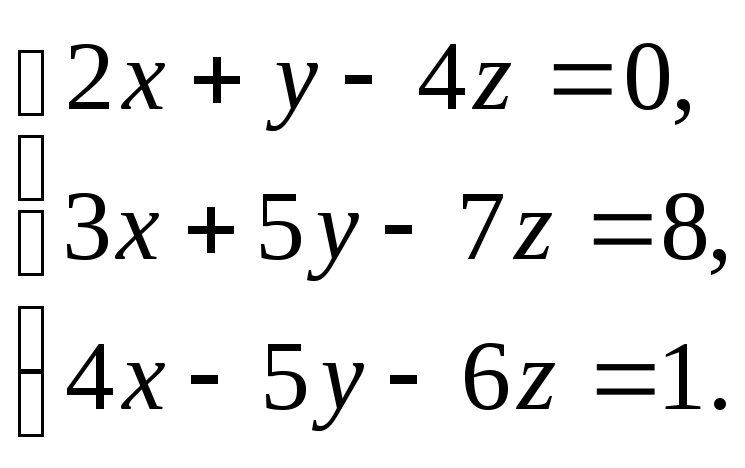
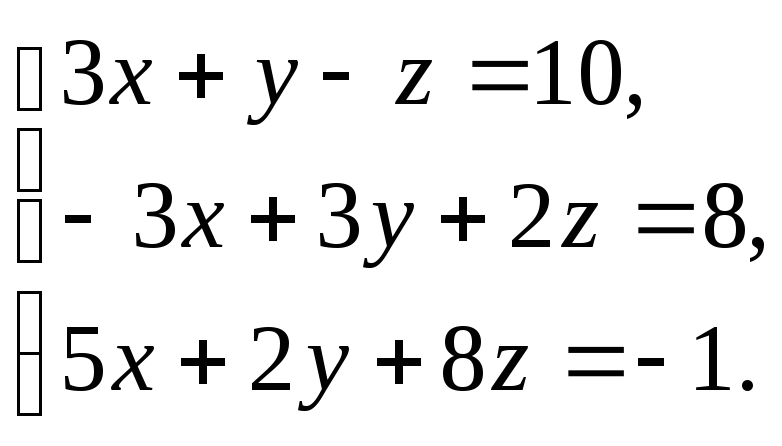
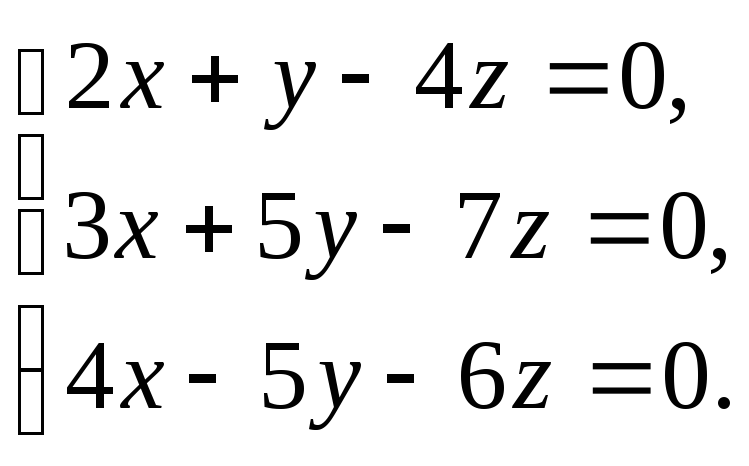
 ,
,
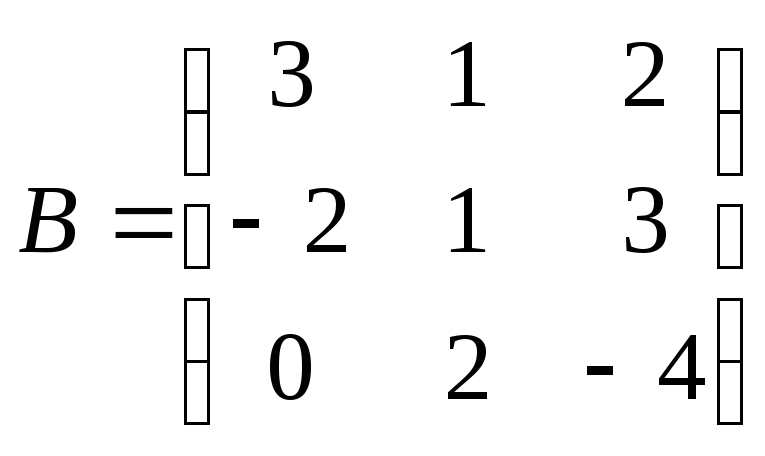 .
.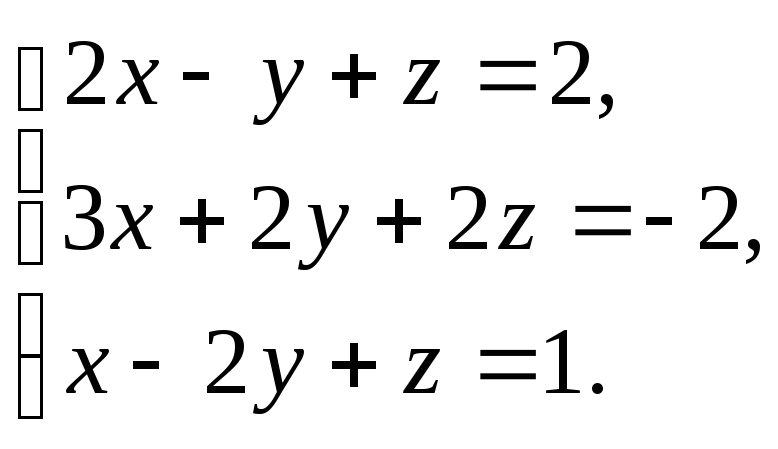
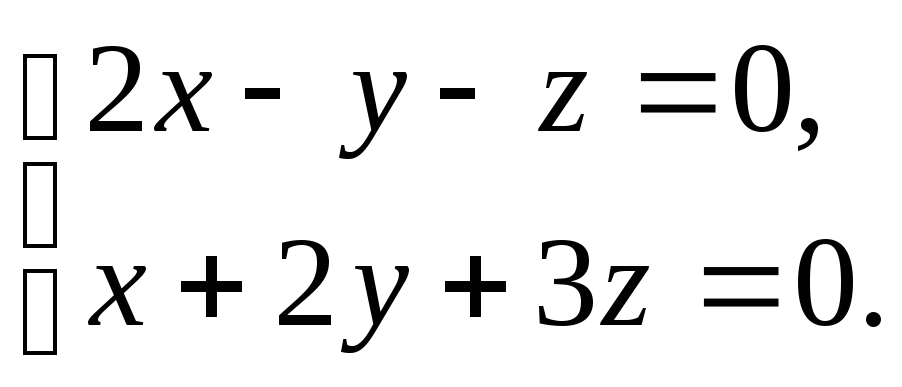
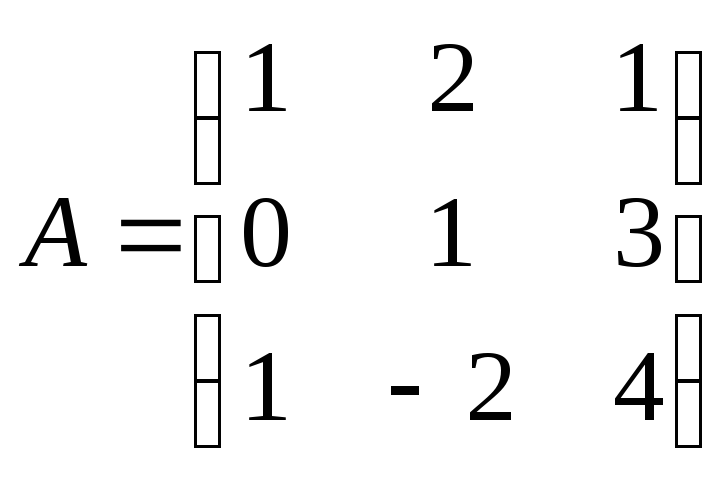 ,
,
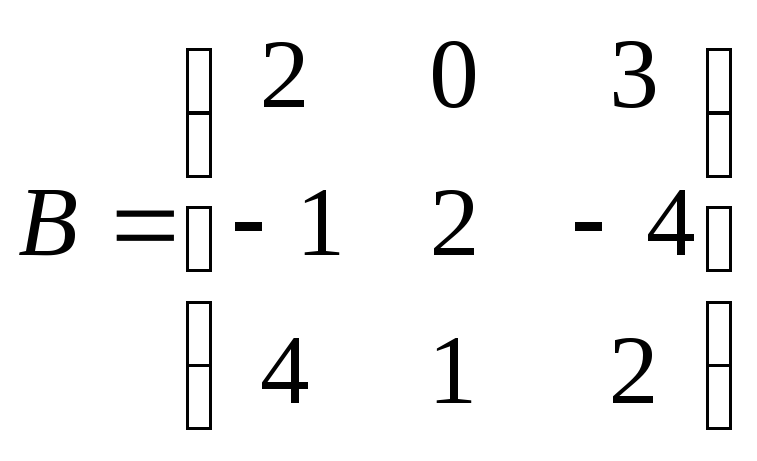 .
.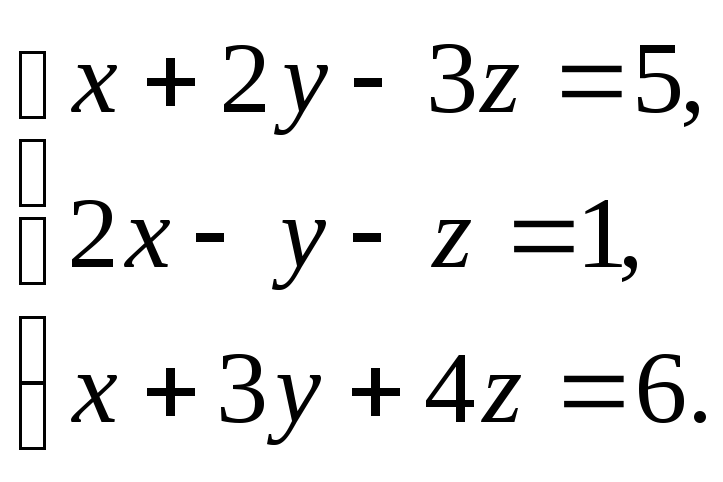
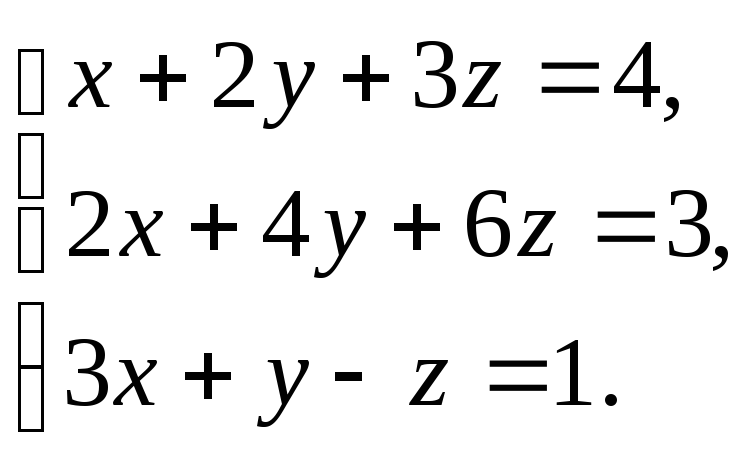
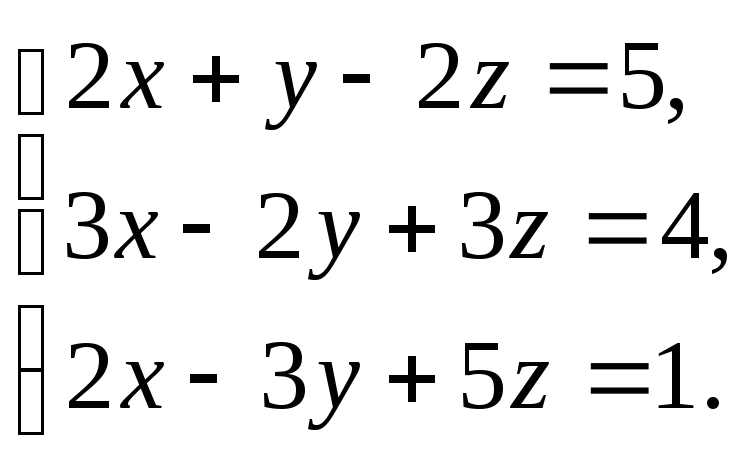
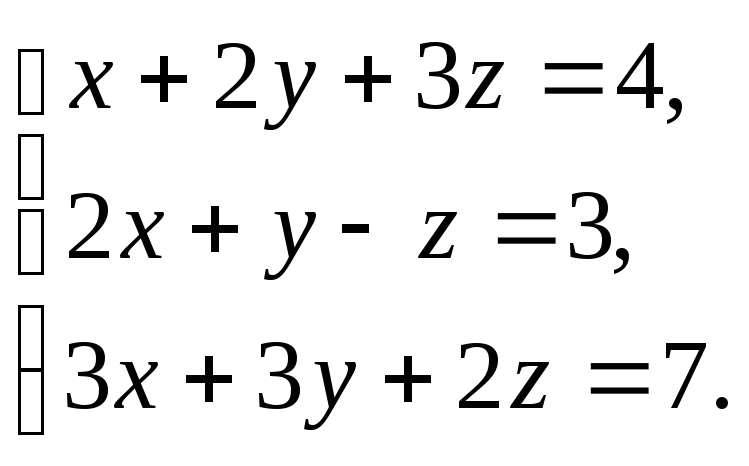
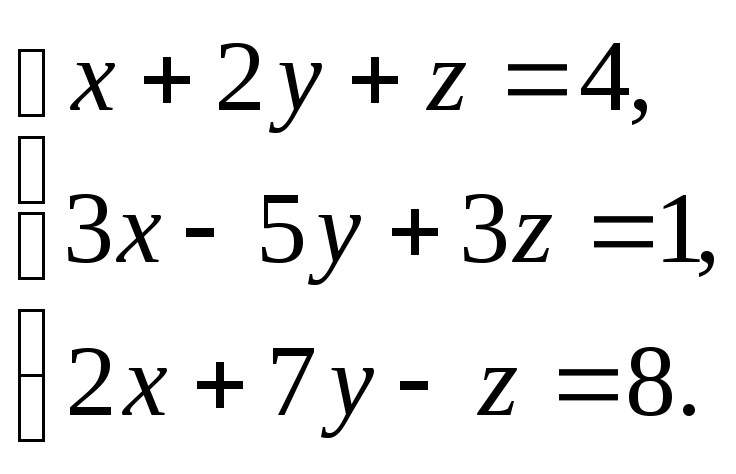
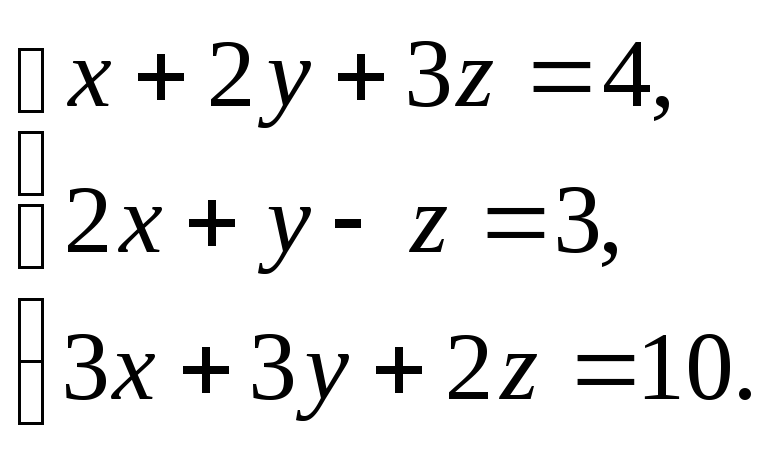
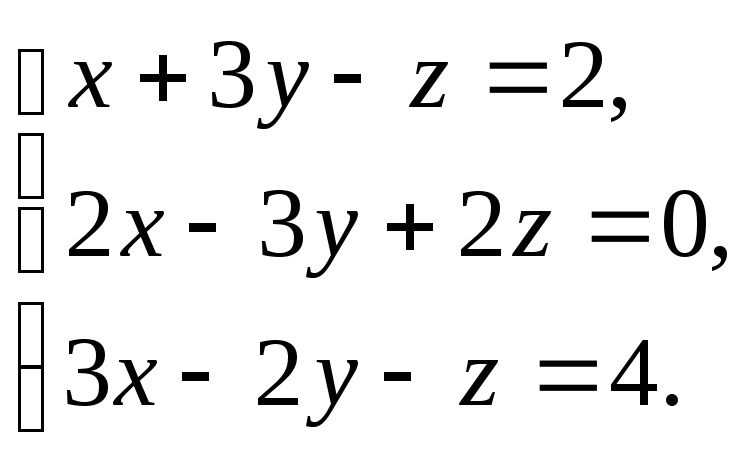
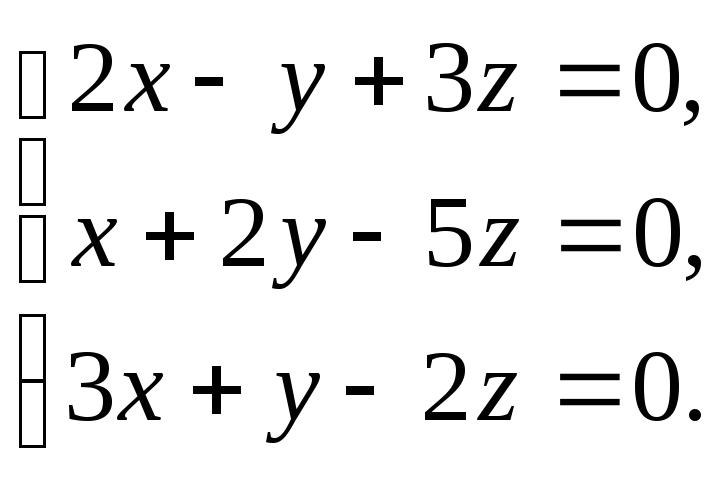
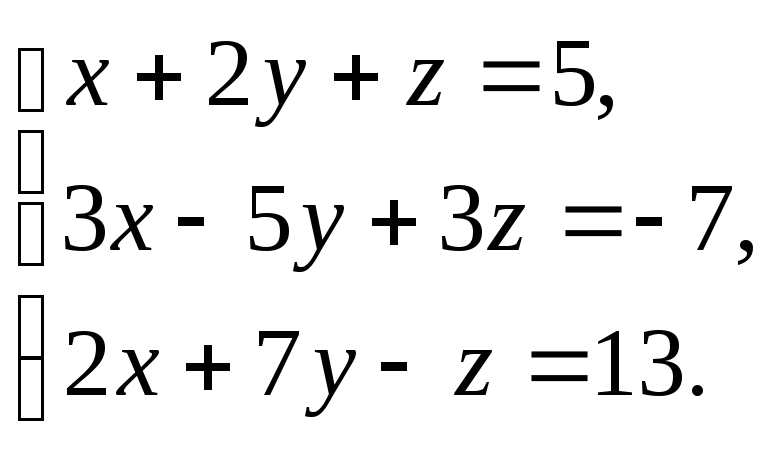

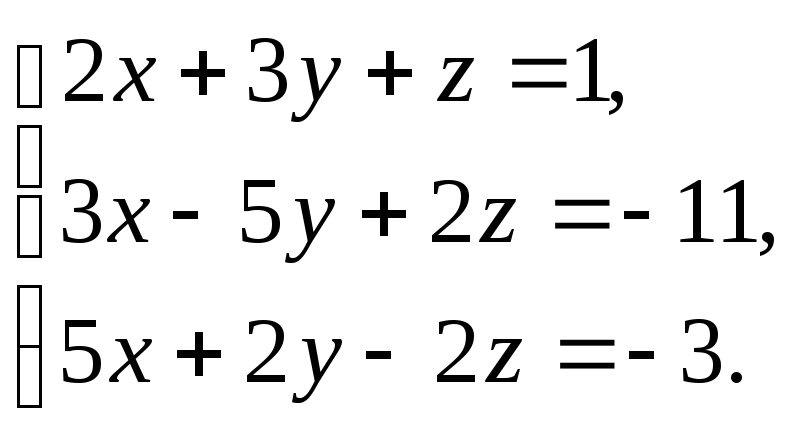

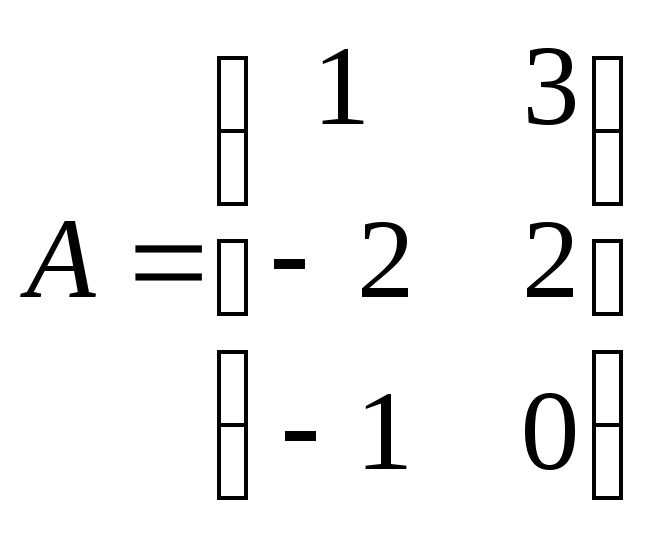 ,
,
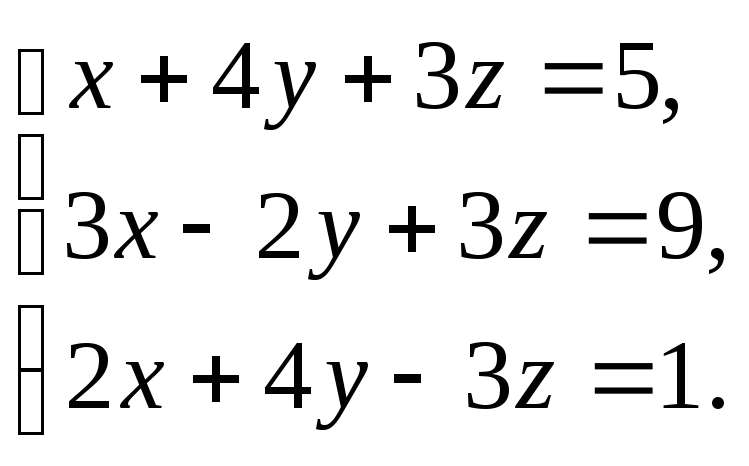

 ,
,
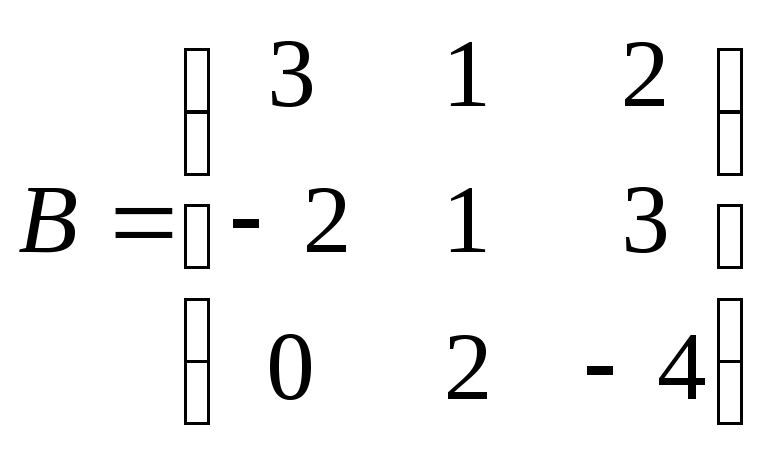 .
.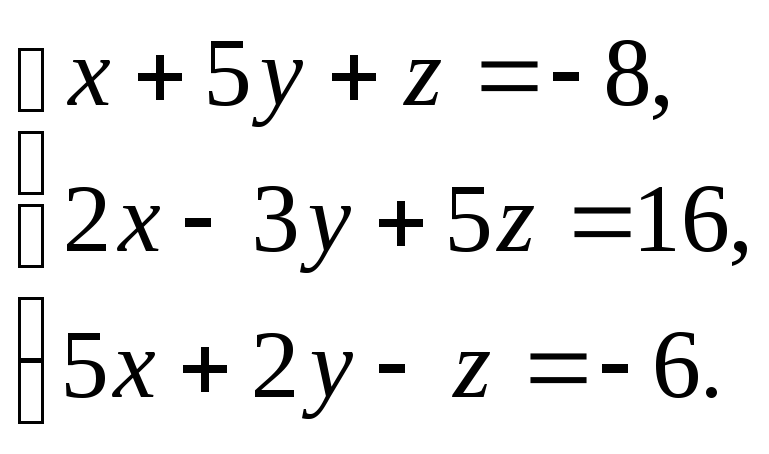
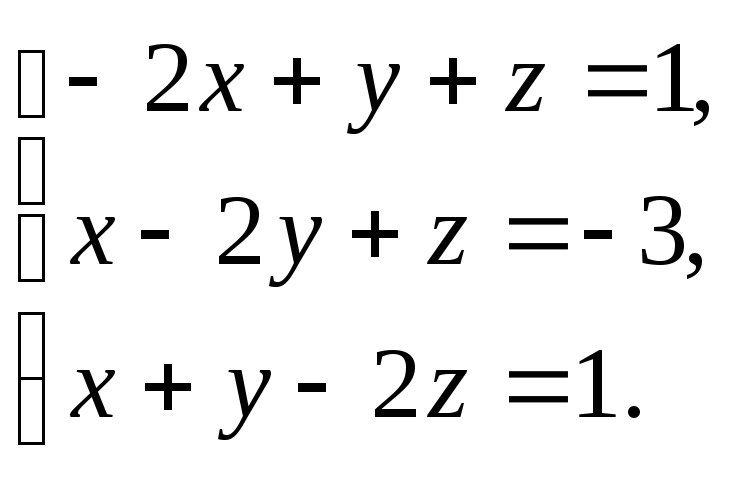
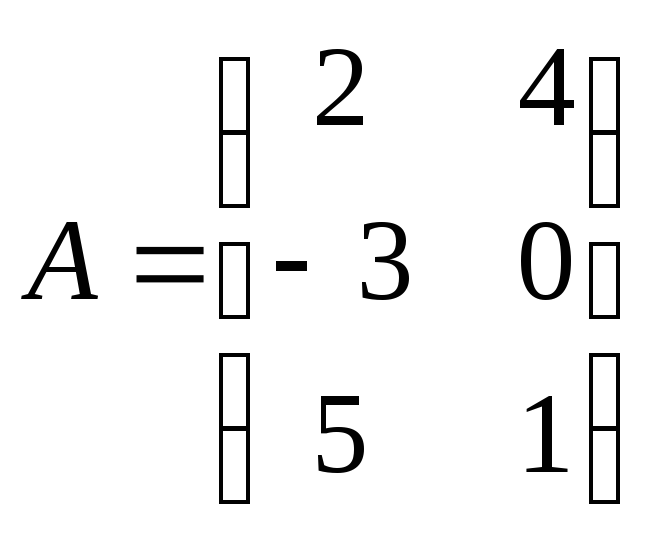 ,
,

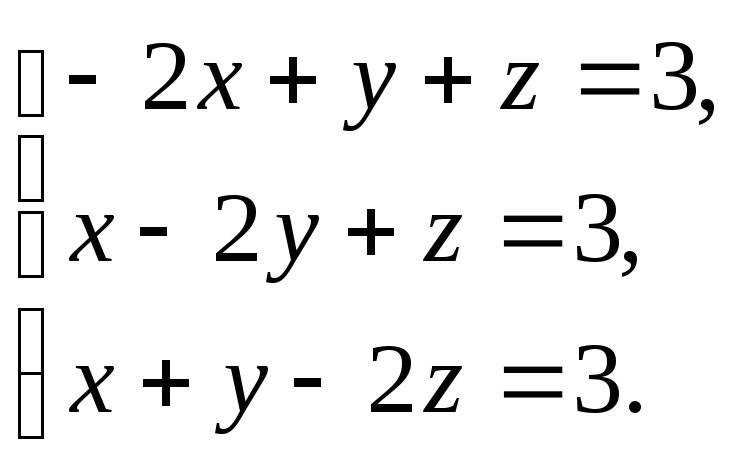
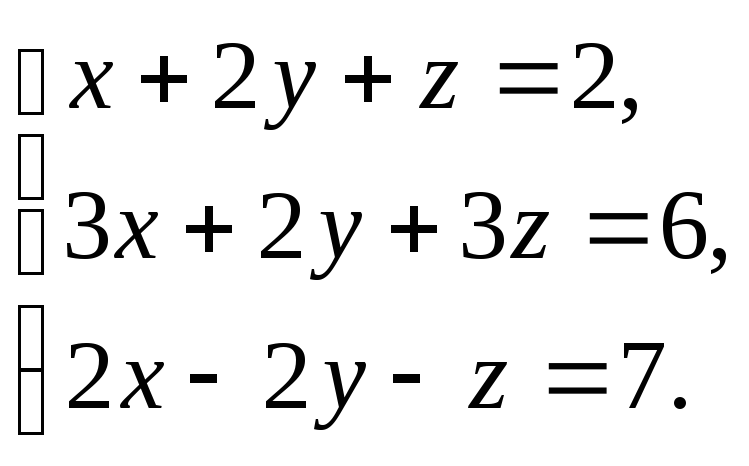
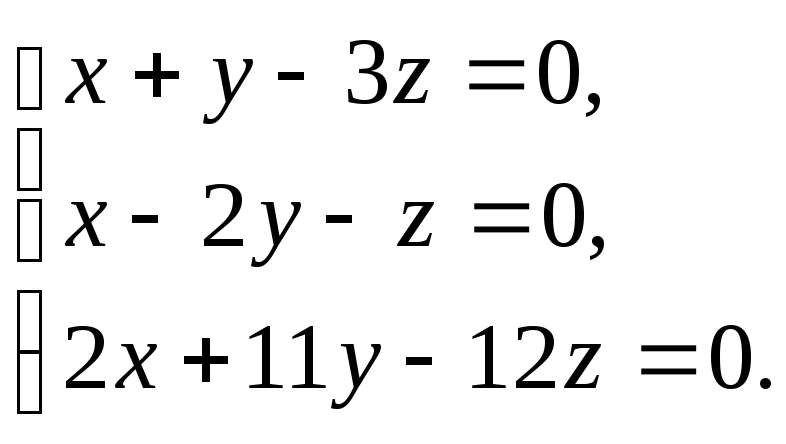
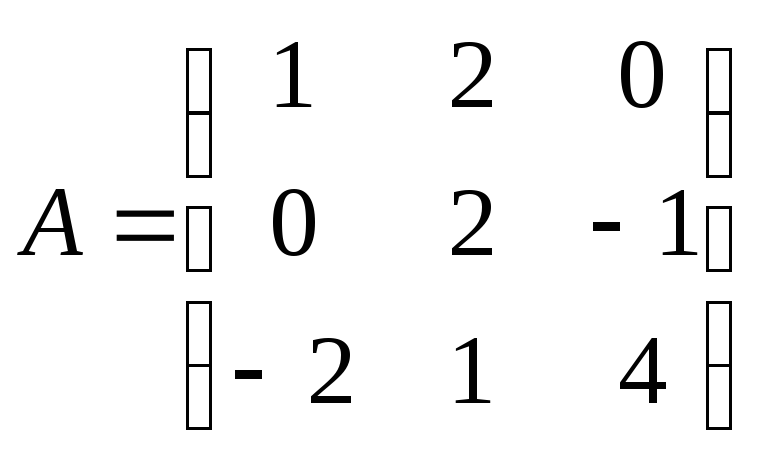 ,
,
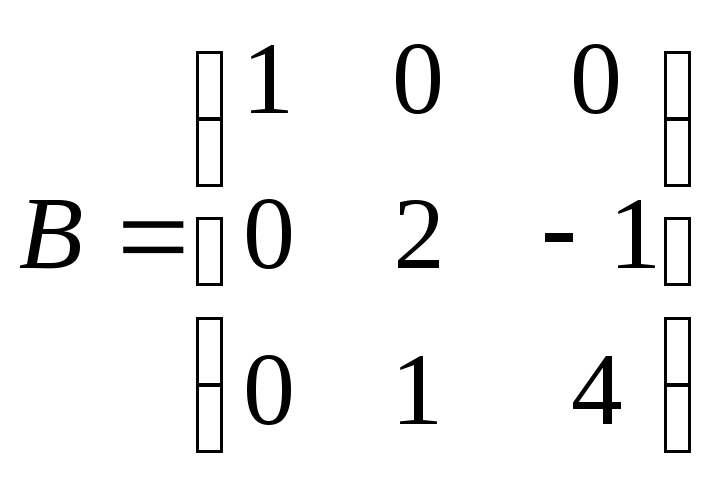 .
.