
- •Предисловие
- •Cвойства определителей
- •9). Определитель равен сумме произведений элементов какой-либо строки или столбца на соответствующие алгебраические дополнения элементов этих строк или столбцов.
- •Собственные числа и собственные векторы матрицы
- •Лекция. 3 Матричная запись и матричное решение систем уравнений 1-го порядка. Ранг матрицы.
- •Другой метод нахождения ранга матрицы
- •Лекция 4. Общая теория решения систем линейных уравнений.
- •Формулы крамера
- •Линейные однородные системы
- •Понятие базиса. Аффинные координаты
- •Декартова система координат ( д.С.К.)
- •Условия коллинеарности двух векторов
- •Деление отрезка в данном отношении
- •Определение. Скалярным произведением векторов и называется число, равное произведению модулей этих векторов на косинус угла между ними.
- •Лекция 8. Выражение векторного произведения через координаты перемножаемых векторов . Смешанное произведение.
- •Уравнение поверхности и линии в пространстве
- •Различные виды уравнения прямой на плоскости
- •Уравнение прямой в отрезках.
- •0 X ; ,m) ; пусть
- •Уравнение пучка прямых
- •Уравнение плоскости в отрезках
- •Уравнение плоскости в нормальном виде
- •Расстояние от точки до плоскости
- •Центриситет эллипса. ,
- •Лекция14. Поверхности второго порядка
- •Построение поверхностей по их уравнениям методом сечений
- •Поворот осей координат
- •Упрощение общего уравнения кривой второго порядка
- •Квадратичные формы
- •Понятие функции
- •Способы задания функции
- •Предел функции при X
- •Предел функции при X
- •Лекция17. Основные теоремы о бесконечно малых функциях и о пределах при X , X x0 , X
- •Определение.
- •Свойства непрерывных функций на отрезке
- •Лекция 20. Комплексные числа , действия над комплексными числами.
- •Алгебраическая форма комплексного числa
- •Тригонометрическая форма комплексного числа
- •Дифференцируемость функции
- •Лекция 24. Дифференциал функции.
- •Дифференциалы высших порядков
- •Математический анализ
Понятие базиса. Аффинные координаты
Определение.
3 линейно независимые вектора
 образуют в пространстве базис , если
любой вектор
образуют в пространстве базис , если
любой вектор
 может быть представлен в виде некоторой
линейной комбинации векторов
, то есть
может быть представлен в виде некоторой
линейной комбинации векторов
, то есть
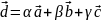 .
(1)
.
(1)
Это разложение вектора в базисе .
Определение.
Числа
 называются координатами вектора
в базисе
называются координатами вектора
в базисе
 то есть координаты вектора это коэффициенты
линейной зависимости , выражающие данный
вектор через данный базис.
то есть координаты вектора это коэффициенты
линейной зависимости , выражающие данный
вектор через данный базис.
Определение. Базис , в котором векторы произвольны называется аффинным . 23
Теорема 1. Всякий вектор может единственным образом разложен в данном базисе.
Доказательство. Пусть
(1)
и ещё есть разложение
 (2)
(2)
Вычтем
из (1) (2) 0 =
 , так как
- базис , то эта линейная комбинация
выполняется тогда, когда
, так как
- базис , то эта линейная комбинация
выполняется тогда, когда


 отсюда
отсюда
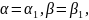
 ,
то есть разложения совпадают ч.т.д.
,
то есть разложения совпадают ч.т.д.
Определение. Три некомпланарных вектора с общим началом О называются аффинным базисом и обозначается { O, }.

= {

O
Определение.
Вектор
 ,
соединяющий начало и точку М, называется
радиусом вектором точки М.
,
соединяющий начало и точку М, называется
радиусом вектором точки М.
Декартова система координат ( д.С.К.)
Определение.
Аффинный базис { O,
}
, у которого векторы
лежат на взаимно ортогональных осях и
длины равны единицы, называется декартовым
ортогональным базисом , принято обозначать
{ 0,
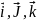 }.
}.
В
силу теоремы о разложении вектора в
базисе для д.с.к.
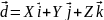
X,Y,Z
– координаты вектора ,
 – орты .
– орты .
Теорема. Декартовы прямоугольные координаты X,Y,Z вектора равны ортогональным проекциям этого вектора на оси OX, OY, OZ соответственно.
Доказательство. Сделаем рисунок
Z



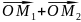
M
=
+
 xOM
;
xOM
;
k
 y
OM;
y
OM;
o
j
 y
y
 z
OM;
z
OM;
i по построению.
 P
P
x 24
 ;
;
 ;
;
 , так как коллинеарны.
, так как коллинеарны.
xOM
=
 °
° =
=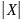 ;
y
OM=
;
y
OM=

z
OM =
 ч. т. д.
ч. т. д.
Определение. Проекции вектора на оси координат называются декартовыми прямоугольными координатами вектора.
Теорема
 Линейные операции над векторами
сводятся к точно таким же линейным
операциям над их одноимёнными координатами.
Линейные операции над векторами
сводятся к точно таким же линейным
операциям над их одноимёнными координатами.
Пример.
Найти координаты вектора
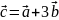 , если
, если
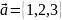 ;
;

Решение.
По теореме
xc=1+3 =1;
yc
=2+3
=1;
yc
=2+3 -13;
zc =
3+3
3=
12
-13;
zc =
3+3
3=
12
Ответ. = {1, -13, 12}.
Определение. Радиус вектор –
это вектор , соединяющий начало координат
и точку А , обозначается
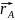 =
{ X,Y,Z}.
=
{ X,Y,Z}.
ЛЕКЦИЯ 6. Длина вектора. Направляющие косинусы.
Пусть вектор
 , так как он является диагональю
параллелограмма , то по теореме из школы
, так как он является диагональю
параллелограмма , то по теореме из школы
 2
=
2
= 2
=
2
=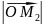 2
=
2
= 2
или
2
= X2 +Y2
+Z2 отсюда
2
или
2
= X2 +Y2
+Z2 отсюда
 (1)
(1)
Рассмотрим
вектор
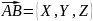 ; точки А(
; точки А( и В (
и В (
z A
B

 ;
;
 ;
={
;
={
 }
,
}
,
k
так как
 и
и
 - проекции , то
- проекции , то
x
i j
y
= {
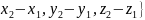 , a модуль вектора
, a модуль вектора
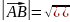
Обозначим углы наклона вектора c осями координат ox,oy,oz соответственно .
Определение.
Косинусы углов, образованных между
вектором и осями координат , называются
направляющими косинусами вектора

z
Если вектор
={
x,y,z}
, то x =
 ;
;



 y=
y= ; z =
; z =
 , как проекции ,отсюда
, как проекции ,отсюда
x o
y
 ,
,
 или
или
 =
=
 ;
;
 =
=
 ;
;
 =
=
 (1)
(1)
Возведём в квадрат обе части равенств (1) и сложим , получим
25
co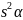 + co
+ co +co
+co =
=
 +
+
 +
= 1.
+
= 1.
 условие того , что
условие того , что
 углы вектора с осями координат.
углы вектора с осями координат.
