9). Определитель равен сумме произведений элементов какой-либо строки или столбца на соответствующие алгебраические дополнения элементов этих строк или столбцов.
Находить алгебраические дополнения таким образом нерационально, есть дру-
гой способ.
Определение. Минором данного элемента определителя n-го порядка называ- ется определитель ( n – 1 ) –го порядка , получаемый из данного определителя путём вычёркивания той строки и того столбца на пересечении которых стоит данный элемент.
Минор элемента
=
=
=
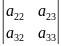, а минор элемента
=
=
=
-
.
Сравним эти миноры с алгебраическими
дополнениями этих же элементов. Приходим
к выводу, что миноры и алгебраические
дополнения с точностью до знака совпадают,
аналитически это выражается формулой
Замечание. Сумма произведений элементов какой –либо строки или столбца на алгебраические дополнения элементов другой строки или столбца равна 0.
Вывод: девятое свойство является способом вычисления определителей порядка выше третьего.
Пример. Применяя свойства , вычислить определитель 4-го порядка.
D
=
Решение. Произведём следующие действия: 1) из элементов 1-й строки вычтем утроенные элементы 2-й строки; 2) к элементам 3-й строки прибавим удвоенные элементы 2-й строки; 3) из элементов 4-й строки вычтем элементы 2-й строки. Тогда исходный определитель преобразуется к виду
D
=
.
Разложим этот определитель по элементам 1-го столбца:
D
= -
.
Прибавляя к элементам 1-й строки элементы 3-й строки и вычитая из элементов 2-й строки элементы 3-й строки, получим
7
D
= -
.
Разложим определитель по элементам 1-го столбца:
D
= -
= 70.
Определение. Определитель, у которого элементы , стоящие ниже или выше диагонали все нули , имеет диагональный вид.
Примеры.
.
Лекция 2 . Понятие матрицы. Основные операции над матрицами. Собственные числа и собственные векторы матрицы.
Определение.Матрицей называется прямоугольная таблица из m строк и n столбцов элементов некоторого множества.
m
n
- порядок матрицы. Если m=n
, то матрица называется квадратной , m
n
– прямоугольной. Обозначается:
A
=
или A
=
, или A
=
Коротко
А =
(i
=
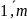j
=
) , числа
- элементы матрицы.
(
)
- матрица строка;
- матрица столбец.
Если m = n , то матрица называется квадратной, если m ≠ n , то матрица прямоугольная.
Определение. Определитель, составленный из элементов квадратной матрицы называется определителем матрицы.
Если матрица
A
=
, то определитель
=
Если ≠ 0 , то матрица называется невырожденной; если = 0 ,то матрица называется вырожденной.
8
A
=
– нуль матрица . E
=
- единичная диагональная матрица.
Порядок матрицы обозначается так : m n , где m – количество строк , а n - количество столбцов.
ОСНОВНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ
Определение. Две матрицы A и B называются равными ( A = B ) , если они имеют одинаковое число строк и столбцов и их соответствующие элементы совпадают.
=
;
≠
; ( 1 2 3) ≠
.
1).
Суммой
2-х матриц A
=
и B
=
( i
=
;
j=
) называется матрица C
=
, ( i
=
; j
=
) ,того же порядка, где
=
+
,т.е.
С=A+B.
Если
A
=
и B
=
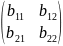, то С =
или
+
=
CВОЙСТВА СЛОЖЕНИЯ
а). А + В = В + А.
б). ( А+ В) +С = А + ( В + С ).
2). Умножение матрицы на число.
Определение.
Произведением матрицы
А =
(i
=
;
j
=
)
на вещественное число
называется матрица С =
(i=
; j
=
) , т.е.
С = А. Пусть матрица
А
=
, тогда матрица
А
=
.
СВОЙСТВА ПРОИЗВЕДЕНИЯ НА ЧИСЛО
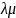а).
А =
(
А).
9
б). ( А + В ) = А + В.
в). ( + ) А = А + В.
г).
0
А
= 0
д). С = А-В это С = А + (-1)В.
3). Умножение матриц.
А
=
и B
=
C
= A∙B
=
Определение.
Произведением матрицы
А =
, ( i
=
j
=
) на матрицу В =
( i
=
; j
=
) называется матрица С =
, ( i
=
),
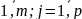имеющая порядок m p , элементы определяются формулой
i = 1,2,
m ; j = 1,2,
p. С = А ∙ В
(1)
=
=
+
+
Вывод. Матрицу А можно умножить на матрицу В , если число столбцов матрицы А равно числу строк матрицы В и получается матрица , у которой , столько строк сколько их имеет матрица - множимое и столько столбцов , сколько их имеет матрица - множитель.
Пример. Перемножить матрицы.
Решение.
=
СВОЙСТВА ПРОИЗВЕДЕНИЯ
а). А∙В ≠ В ∙ А.
б). А ( ВС) = ( АВ )С.
в). (А + В )С = АС + ВС.
ОБРАТНАЯ МАТРИЦА .
Определение. Матрица , у которой строки заменены столбцами , называется транспонированной по отношению к первой матрице.
А
=
=
10
Определение.
Матрица
,
составленная из алгебраических дополнений
к элементам матрицы
называется присоединённой
к матрице А или
взаимной.
Определение.
Обратной матрицей
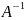к квадратной матрице А называется
матрица , удовлетворяющая условию
Элементами
обратной матрицы являются алгебраические
дополнения элементов присоединённой
матрицы
, делённые на число , равное определителю
матрицы А , т. е. det
A
=
=
=
.
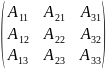Из этой формулы следует, что обратную матрицу имеет только невырожденная матрица.
Пример.
Найти обратную матрицу для матрицы
A
=
Решение. Вычислим сначала определитель матрицы А.
= 4+0+0 – 0 -1 – 12 = - 9,
определитель матрицы не равен нулю ,
поэтому матрица А имеет обратную. Находим
алгебраические дополнения.
= 3
= - 4
= 2
=-6
= 2
= - 1
=
.
= 3
= - 1
= -4
Чтобы проверить вычисления , найдём А .
А
=
=
= Е .