Квадратичные формы

Определение. Квадратичной формой Q ( x ) в n-мерном пространстве называется скалярное произведение следующего вида : Q ( 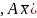, если = ( ,если же , то ( =

= , то есть Q ( ,где .

Определение. Квадратичная матрица называется симметричной , если она не меняется при транспонировании , то есть

Пусть n=3 , A = если n=2 , то Q ( .

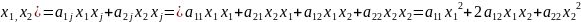Определение. Канонической квадратичной формой называется квадратичная форма , содержащая только квадраты переменных.

Если n = 2 , то Q ( 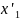, , где 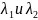собственные числа матрицы А = . С помощью квадратичных форм можно кривые второго порядка приводить к каноническому виду , а также определять тип кривой.

Определение. Кривые второго порядка : эллипс , гипербола , парабола задаются квадратичными формами в двумерном пространстве , причём , если :

1). - эллипс.

2). 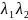, то – гипербола .

3). = 0 , то – парабола.

Пример 1. Определить тип кривой второго порядка , заданной уравнением:

Решение. Составим симметрическую матрицу из коэффициентов при переменных А = , характеристическое уравнение на собственные числа имеет вид = ( 1 - = 0 , . = . Ответ. Кривая - эллипс.

Пример 2. Определить тип кривой второго порядка : xy = 1.

60

Решение. Матрица А = ; = = 0, Произведение = . Ответ. Кривая - гипербола .

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Лекция 16. Понятие множества, функции, предела функции.

Понятие множества

Определение. Множество – это совокупность каких – либо объектов . Обозначаются множества А , В , М… . Элементы множества обозначаются a,b,c ,x ,y … .

Если элемент принадлежит множеству,то x Є M , если не принадлежит,то x M.

Определение. Объединением или суммой множеств М_i называется множество М всех элементов , принадлежащих хотя бы одному из множеств М_{i .}

Обозначается: М = М₁ М₂ … М_n или М =

М₁

М₂

М₃

М₄

ММ

М = М₁ М₂ М₃ М₄

Определение. Пересечением множеств М₁ , М₂ …..М_n называется множество

М = М₁ М₂ М₃ … М_n , которому принадлежат элементы всех множеств М_n одновременно.

М₁

М₂

М

М = М₁ М₂

Символ _x означает ‘’ для всех x ‘’ или ‘’ для каждого x ‘’ или ‘’каково бы ни было x “,” для любого x “ . Символ _x читается “ существует такое x ,что “ или “ для некоторых x “. А В из А следует В ; А В из А следует В и наоборот из В следует А.

61