Уравнение плоскости в отрезках

Рассмотрим общее уравнение плоскости Ax + By + Cz + D = 0. Перенесём D вправо и разделим на D: 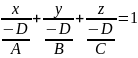, обозначим

= b, уравнение примет вид: уравнение плоскости в

отрезках, где a, b , c отрезки , которые плоскость отсекает от осей координат.

Пример. Построить плоскость 2 x + 5 y – 10 = 0. Приведём это уравнение к уравнению в отрезках На оси ox отложим отрезок x = 5, на оси oy отложим отрезок y = 2. z

o 2 y

x 5

Лекция 11. Угол между плоскостями . Условия параллельности и перпендикулярности плоскостей.

Плоскости заданы общими уравнениями. и

=

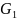1). Если 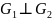, то ( или в координатах

→условие перпендикулярности плоскостей.

42

2). Если , то в координатах →условие параллельности плоскостей.

Пример 1. Составить уравнение плоскости , проходящей через точку параллельно плоскости 3x + 2y – 7z +8 = 0.

Решение. 3(x+2y) + 2(y-1) – 7(z-4) = 0. Ответ. 3x + 2y - 7z +14 = 0

Пример 2. Через точку провести плоскость , перпендикулярную плоскостям

Решение. Уравнение плоскости находим по формуле уравнения плоскости , проходящей через точку , то есть А(x + 2) + B(y – 3) + C (z – 6)=0. Из рисунка вид-

но , что нормальный вектор иско-

мой плоскости перпендикулярен

нормальным векторам данных

плоскостей . ⊥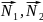 , поэтому

= = = 13 .

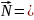{ 13 , -8 , 1 } .Ответ.

Уравнение плоскости , проходящей через 3 различные

точки ,не лежащие на одной прямой

; ; ;

.М . М( x,y,z). Соединим эти точки векторами , усло-

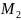. вие принадлежности 3-х векторов одной плоскос-

. ти- равенство нулю их смешанного произ-

ведения ( , или в коор-

динатах

= 0 →уравнение плоскости, проходящей через

3 – и точки.

Пример. Получить уравнение плоскости , проходящей через три известные точки :

Решение. Найдём координаты векторов ; ; 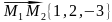. Уравнение плоскости запишем в виде:

43

= 0 , раскрываем определитель по элементам 1-й строки ,

получаем (x-1)5 – (y+1)(-5) + z 5 =0 или 5x+5y +5z =0. Ответ. x+y+z =0 .