Статические звенья

К статическим относятся такие звенья, которые при ступенчатом входном воздействии переходят из начального положения равновесия в новое равновесное состояние.

Статические звенья делятся на:

1) Пропорциональные;

2) Апериодические первого порядка;

3) Апериодические второго порядка;

4) Колебательные.

1. Пропорциональное звено

Это звено называют также усилительным и безынерционным. Звено описывается алгебраическим уравнением:

х_вых = kх_вх, [3.1]

где k - коэффициент передачи (усиления), имеющий размерность: единицы выходной величины, делённые на единицы входной величины (та­кую размерность имеют коэффициенты передачи всех статических звень­ев).

Передаточная функция звена W(p) = k . [3.2]

Переходная функция h(t) = k₁(t). [3.3]

Представляет собой ступенчатую функцию высотой k (рис. 3.1)

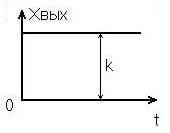
Рис. 3.1. Переходная функция пропорционального звена

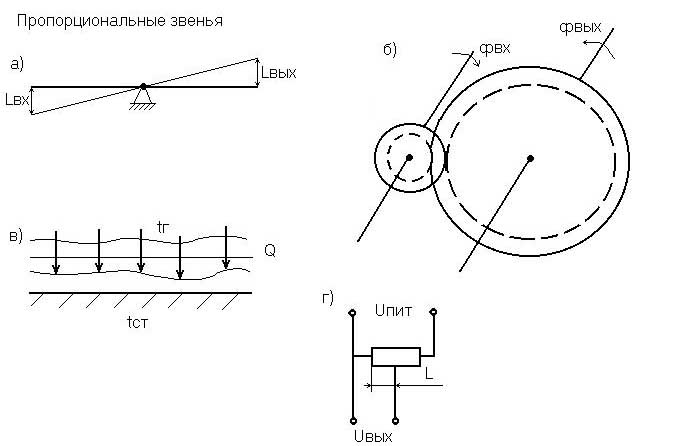
Рис. 3.2. Примеры пропорциональных звеньев

Примерами пропорционального звена могут служить: рычаг (рис. 3.2,а), если входная величина перемещение (усилие) на одном конце рычага, а выходная величина – перемещение (усилие) на втором конце; зубчатая передача (редуктор), если х_вх = _вх – угол поворота малой шестерни, а х_вых = _вых – то же для большой шестерни (рис. 3.2,б); тепло­отдача конвекцией от движущегося газа к стенке, если х_вх - разность температур газа и стенки t = t_г – t_ст, а х_вых - количество отдавае­мого тепла Q (рис. 3.2,в); потенциометрический датчик измерительного прибора, если х_вх - перемещение движка реохорда L, а х_вых - снимаемое о датчика напряжение U_вых (рис. 3.2,г).

Обычно пропорциональное (безынерционное) звено является некоторой идеализацией реальных звеньев, и к нему сводятся позиционные звенья, рассмотренные ниже, если можно пренебречь переходными процессами в них. В этих условиях, например, большинство датчиков самых различных физических величин относятся к пропорциональному звену.

2. Апериодическое (инерционное) звено первого порядка

Описывается дифференциальным уравнением:

, [3.4]

где k – коэффициент передачи;

Т – постоянная времени, с.

Передаточная функция звена W(p) = k/(Tp + 1); [3.5]

Переходная функция звена h() = k (1 – е^-/T). [3.6]

Переходная функция представляет собой экспоненту (рис. 3.3). Отрезок, отсекаемый касательной, проведенной в начальной точке, при установившемся значении выходной величины равен постоянной времени Т.

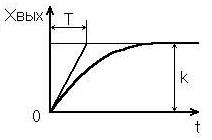
Рис. 3.3. Переходная функция апериодического звена 1-го порядка

Постоянная времени - это время, за которое выходная величина достигла бы своего установившегося значения, если бы с постоянной начальной скоростью. Чем больше Т, тем длительнее переходный процесс. Строго говоря, установившееся значение Х_вых = k достигается при   , но практически переходный процесс считается закончившимся через время   3Т.

Постоянная времени характеризует "инерционность" апериодического звена. Если она мала, то апериодическое звено по существу становится безынерционным.

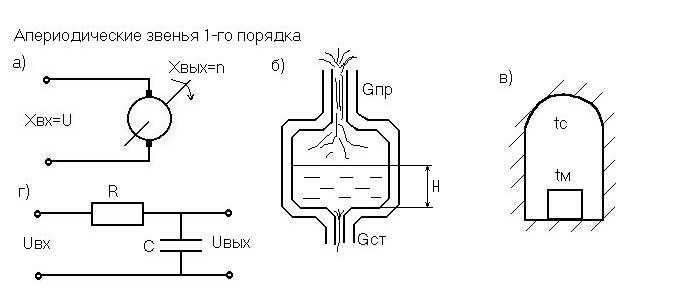
Рис. 3.4. Примеры апериодических звеньев 1-го порядка

Примерами апериодических звеньев могут служить: электропривод постоянного токи, если входная величина - подводимое напряжение х_вх = u, а выходная величина х_вых = n - скорость вращения (рис. 3.4,а); проме­жуточный ковш МНЛЗ, если х_вх = G_пр - G_cт - разность поступления и расхода жидкого металла, а х_вых = Н - уровень металла в ковше (рис. 3.4,6); нагрев тела, помещённого в среду с температурой t_c (теплоотдача оце­нивается по закону Ньютона q = (t_c – t_м), где q - плотность теплового потока на нагреваемое тело;  - коэффициент теплоотдачи), если t_c.- входная величина, а средняя температура тела t_м - выходная величина (рис. 3.4,в); цепочка RC (рис. 3.4,г), если х_вх = u_вх – подводимое напряжение, х_вых = u_вых – снимаемое напряжение.

3. Апериодическое (инерционное) звено второго порядка

Описывается уравнением:

. [3.7]

Для этого звена корни характеристического уравнения p² +T₁p +1 = 0 должны быть действительными, что выполняется при условии: Т₁ > 2Т₂.

Передаточная функция звена W(p) = k/( p² +T₁p +1). [3.8]

Знаменатель передаточной функции может быть разложен на множите­ли. и тогда передаточная функция будет иметь вид:

W(p) = k/[(T₃p+1)( T₄p+1)], [3.9]

где .

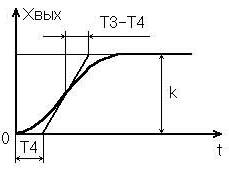
Рис. 3.5. Переходная функция апериодического звена 2-го порядка

Переходная функция (рис. 3.5) может быть получена по формуле Хевисайда

. [3.10]

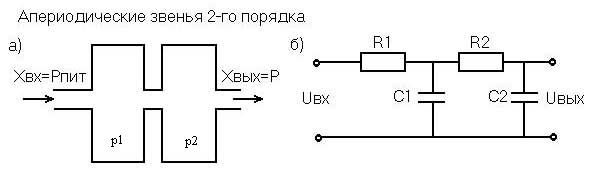
Рис. 3.6. Примеры апериодических звеньев 2-го порядка

Примеры апериодического звена второго порядка: последовательное соединение двух пневматических ёмкостей, если входная величина х_вх = Р_пит, а выходная величина - давление в емкости х_вых = р (рис. 3.6,а); цепочка RC (рис. 3.6,б), если х_вх = u_вх – подводимое напряжение, х_вых = u_вых – снимаемое напряжение.

4. Колебательное звено.

Дифференциальное уравнение звена обычно представляется в виде:

, [3.11]

где  - коэффициент затухания, 0 <  < 1.

Корни характеристического уравнения равны

и у колебательного звена должны быть комплексными. Комплексные корни получаются при  < 1.

Передаточная функция звена: . [3.12]

Переходная функция звена:

. [3.13]

где  = /Т , а носит затухающий колебательный харак­тер около значения х_вых()  k. Ее затухание определяется действи­тельной частью корней характеристического уравнения , а частота - мнимой частью . Существует характеристика переходного процесса, на­зываемая степенью колебательности т = /, которая для колебательного звена находится в интервалах 0 < т < . Колебательность переходного процесса может также характеризоваться степенью затухания:

, [3.14]

где х₁ и х₃ - величины первой и третьей амплитуд выходных колебаний (рис. 3.7).

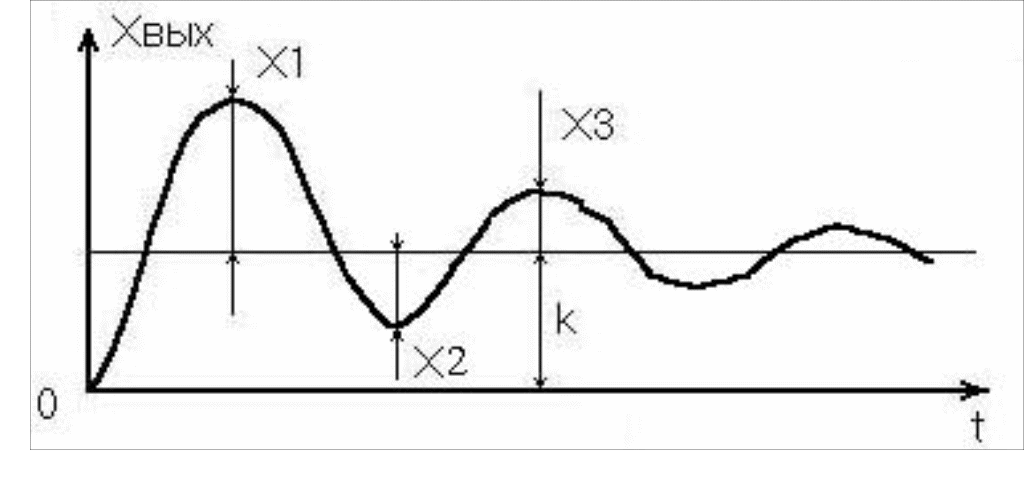
Рис. 3.7. Переходная функция колебательного звена

Значение степени затухания связано с действительной и мнимой час­тями корней характеристического уравнения колебательного звена

, [3.15]

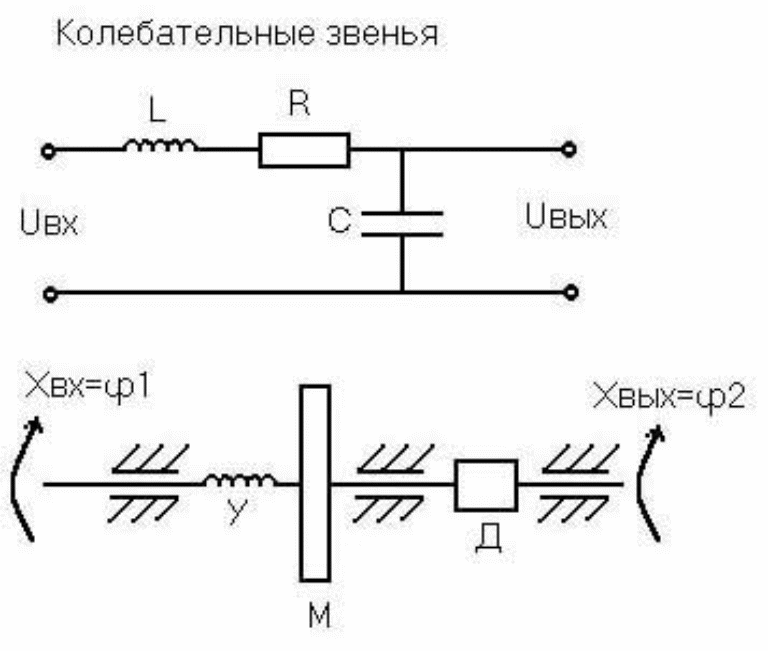
Рис. 3.8. Примеры колебательных звеньев

Примерами колебательных звеньев могут служить колебательный LRC -контур (рис. 3.8,а), если х_вх = u_вх – подводимое напряжение, х_вых = u_вых – снимаемое напряжение и упругая механическая передача (рис. 3.8,б). В передаче имеется упругий элемент У, маховик М и демпфер Д, оказывающий сопротивление вращению вала. Входная величина х_вх - угол поворота входного вала ₁, выходная величина х_вых - угол поворота выходного вала ₂.

АСТАТИЧЕСКИЕ (ИНТЕГРИРУЩИЕ) ЗВЕНЬЯ

Это такие звенья, у которых после поступления на вход ступенчато­го воздействия выходная величина не приходит к установившемуся значе­нию (как у статических), а непрерывно изменяется. Они делятся на 2 вида:

1. Идеальное

2. Реальное

1. Идеальное интегрирующее звено.

Дифференциальное уравнение звена:

, [3.16]

где k₁ – коэффициент передачи, имеющий размерность: единицы скорости изменения выходной величины, делённые на единицы входной величины.

Передаточная функция звена: W(p) = k₁/p. [3.17]

Переходная функция звена: h() = k₁, [3.18]

(рис. 3.9,а) представляет собой прямую линию с углом наклона агсtg k₁.

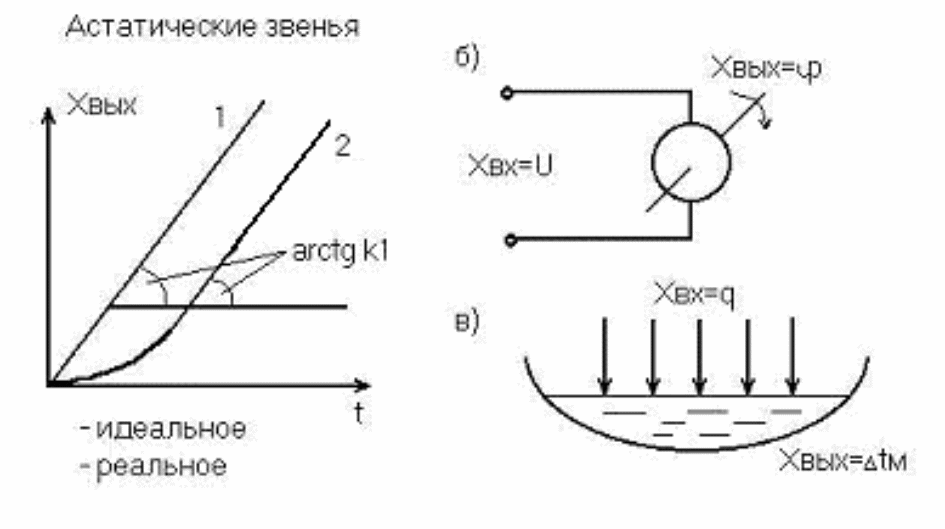
Рис. 3.9. Переходная функция и примеры идеального интегрирующего звена

Примеры интегрирующих звеньев: электродвигатель, если входная ве­личина - напряжение питания, а выходная величина - угол поворота яко­ря  (рис. 3.9,б); кристаллизатор МНЛЗ, если входная величина - рас­ход металла из промежуточного ковша (при постоянной скорости вытяги­вания слитка.), а выходная величина - уровень металла в кристаллизато­ре; ванна жидкого металла в сталеплавильной печи, если входная величина ^- тепловой поток через поверхность ванны q, а выходная величина - изменение средней температуры металла t_м (рис. 3.9,в)

2. Реальное интегрирующее звено (интегрирующее звено с замедлением).

Звено описывается дифференциальным уравнением:

, [3.19]

Передаточная функция звена: W(p) = k₁/p(Tp+1). [3.20]

Переходная функция реального интегрирующего звена: . [3.21]

отличается от переходной функции идеального эвена в начальный момент времени, а затем переходит в прямую линию с тем же углом наклона.

Примерами реальных интегрирующих звеньев могут служить те же звенья, что показаны на рис. 3.9, если более точно, без допущений рассматривать их уравнения движения. Например, электродвигатель с постоянной скоростью будет идеальным интегрирующим звеном. Однако в момент пуска постоянная скорость установится не сразу, а с некоторым замедлением, и электродвигатель следует рассматривать как реальное интегрирующее звено.

ДИФФЕРЕНЦИРУЮЩИЕ ЗВЕНЬЯ.

Делятся на 2 вида: идеальное и реальное.

1. Идеальное дифференцирующее звено.

Дифференциальное уравнение звена

, [3.22]

где k₂ – коэффициент передачи дифференцирующего звена, имеющий размерность: единицы выходной величины, делённые на единицы скорости изменения входной величины.

Передаточная функция звена W(р) = k₂p. [3.23]

Переходная функция звена h() = k₂(), [3.24]

где () - так называемая дельта-функция, которая равна нулю всюду, кроме нулевого момента времени, где её значение стремиться к беско­нечности.

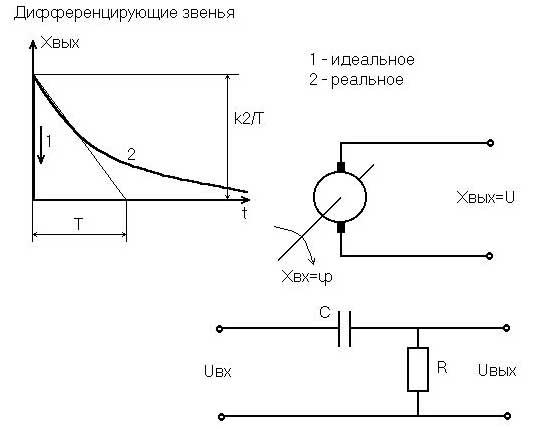
Рис. 3.10. Переходная функция и примеры дифференцирующих звеньев

Переходная функция идеального звена (рис. 3.10,а) представляет собой мгновенный бросок выходной величины в бесконечность в момент нанесения ступенчатого входного воздействия и столь же мгновенное возвращение к нулю.

Наиболее близко к идеальному звену приближается тахогенератор постоянного тока (рис. 3.10,б), если входной величиной считать угол поворота якоря, а выходной - ЭДС якоря, а также операционный усили­тель в режиме дифференцирования, применяемый в аналоговых ЭВМ.

2. Реальное дифференцирующее звено (дифференцирующее звено с замедлением)

Звено описывается дифференциальным уравнением

Передаточная функция звена W(р) = k₂p/(Tр + 1)

Переходная функция звена представляет собой экспоненту, касательная к которой в точке наиболь­шей крутизны отсекает на нулевом значении выходной величины постоянную времени Т (рис. 3.10,а).

Примером реального дифференцирующего звена может служить цепочка RC (рис. 3.10,в), если х_вх = u_вх – подводимое напряжение, х_вых = u_вых – снимаемое напряжение.