Плотность вероятности

Пусть   является вероятностной мерой на  , то есть определено вероятностное пространство  , где   обозначает борелевскую σ-алгебру на  . Пусть  обозначает меру Лебега на  .

Определение 1. Вероятность   называется абсолютно непрерывной (относительно меры Лебега) ( ), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

Если вероятность   абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция   такая, что

,

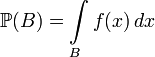где использовано общепринятое сокращение  , и интеграл понимается в смысле Лебега.

Определение 2. В более общем виде, пусть   — произвольное измеримое пространство, а   и   — две меры на этом пространстве. Если найдется неотрицательная  , позволяющая выразить меру   через меру   в виде

то такую функцию называют плотностью меры   по мере  , или производной Радона-Никодима меры   относительно меры  , и обозначают

.

Свойства плотности вероятности

• Плотность вероятности определена почти всюду. Если   является плотностью вероятности   и 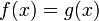  почти всюду относительно меры Лебега, то и функция   также является плотностью вероятности  .

• Интеграл от плотности по всему пространству равен единице:

.

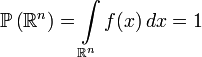Обратно, если   — неотрицательная п.в. функция, такая что  , то существует абсолютно непрерывная вероятностная мера   на   такая, что   является её плотностью.

• Замена меры в интеграле Лебега:

,

где   любая борелевская функция, интегрируемая относительно вероятностной меры  .

Плотность случайной величины

Пусть определено произвольное вероятностное пространство  , и   случайная величина (или случайный вектор).   индуцирует вероятностную меру   на  , называемую распределением случайной величины  .

Определение 3. Если распределение   абсолютно непрерывно относительно меры Лебега, то его плотность   называется плотностью случайной величины  . Сама случайная величина   называется абсолютно непрерывной.

Таким образом для абсолютно непрерывной случайной величины имеем:

.

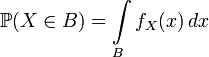Замечания

• Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.

• Функция распределения абсолютно непрерывной случайной величины   непрерывна и может быть выражена через плотность следующим образом:

.

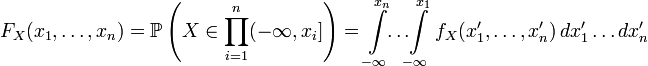В одномерном случае:

.

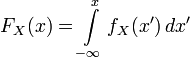Если  , то  , и

.

В одномерном случае:

.

• Математическое ожидание функции от абсолютно непрерывной случайной величины может быть записано в виде:

,

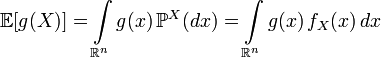где   — борелевская функция, так что   определено и конечно.

Плотность преобразования случайной величины

Пусть   — абсолютно непрерывная случайная величина, и   — инъективная непрерывно дифференцируемая функция такая, что  , где   — якобиан функции   в точке  . Тогда случайная величина   также абсолютно непрерывна, и её плотность имеет вид:

.

В одномерном случае:

.

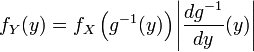Примеры абсолютно непрерывных распределений

• Бета распределение;

• Распределение Вейбулла;

• Гамма распределение;

• Распределение Коши;

• Логнормальное распределение;

• Нормальное распределение;

• Непрерывное равномерное распределение

• Распределение Парето;

• Распределение Стьюдента;

• Распределение Фишера;

• Распределение хи-квадрат;

• Экспоненциальное распределение;

• Многомерное нормальное распределение.

Флуктуация (от лат. fluctuatio — колебание) — термин, характеризующий любое колебание или любое периодическое изменение. В квантовой механике — случайные отклонения от среднего значения физических величин, характеризующих систему из большого числа частиц; вызываются тепловым движением частиц или квантовомеханическими эффектами.

Примером термодинамических флуктуаций являются флуктуации плотности вещества в окрестностях критических точек, приводящих, в частности, к сильному рассеянию светавеществом и потере прозрачности.

Флуктуации, вызванные квантовомеханическими эффектами, присутствуют даже при температуре абсолютного нуля. Они принципиально неустранимы. Пример проявления квантовомеханических флуктуаций — эффект Казимира, а также силы Ван-дер-Ваальса. Непосредственно наблюдаемы квантовомеханические флуктуации для заряда, прошедшего через квантовый точечный контакт — квантовый дробовой шум.

Средние значения физических величин

В классической механике каждая динамическая величина имеет определённое значение. В квантовой механике дело обстоит иначе. Например, система находится в состоянии, которое является результатом суперпозиции состояний   с собственными значениями  .

Если система находится либо в состоянии  , либо в состоянии  , то соответствующее измерение даст определенное число   или   соответственно. Какое значение будет получатся, когда система находится в состоянии

   Обобщенная схема сетевой архитектуры

Здесь в классической физике получилось бы одно строго определённое число.

В квантовой механике получается не одно определённое число, а одно из двух чисел: или  , или   и никаких других. То или другое значение получается не с достоверностью, а лишь с определённой вероятностью. В квантовой механике нельзя приписать динамической переменной определённого значения, но всегда можно приписать определённую вероятность.

А если известны вероятности, то можно вычислить среднее значение.

Среднее значение координаты х.

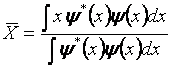
Если волновая функция нормирована к единице, то

  

Учитывая, что оператор координаты “ ”есть просто умножение на х: