Вопросы с выводом формулы и доказательством

1. Формулы полной вероятности.

Определение:

Набор событий Н₁, Н₂,…,Н_n называется полной группой событий, если они попарно несовместны и их сумма составляет достоверное событие:

Н₁, Н₂,…,Н_n = Ω и Ɏ i, j: H_i*H_j = Ø.

Любое событие А может появиться вместе с одним из событий Н₁, Н₂,…,Н_n, образующих полную группу событий. События Н₁, Н₂,…,Н_n называются гипотезами для события А.

Справедлива следующая теорема (формула полной вероятности):

Пусть события Н₁, Н₂,…,Н_n образуют полную группу событий и Р(H_i)>0. Тогда для любого события А:

Р(А) = 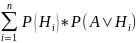(1)

Доказательство:

В силу свойств операций над событиями

А=А*Ω = А*( Н₁, Н₂,…,Н_n) = А* Н₁ + А*Н_2+…+А*Н_n

Поскольку, по условию теоремы, события 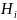попарно несовместны, то и события 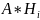тоже попарно несовместны. Тогда, применяя теорему сложения, получим

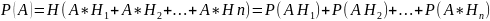(2)

Теперь, используя теорему умножения для зависимых событий, каждое слагаемое в ф.(2) можно подставить в следующем виде:

(3)

Из соотношений ф. (2) и (3) получим утверждение теоремы (1).

2. Доказать свойство дисперсии D(C*X) =C²*D(X)

Для любой случайной величины Х и постоянной С справедлива формула:

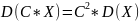
Доказательство:

Из определения дисперсии имеем

D(CX) = M(CX - M(CX))²

Применяя свойство математического ожидания, получаем

M(CX - M(CX))² = M(CX – С*M(X))² = M(C² (X - M(X)²) = C²M(X - M(X))² = С²*D(X).

т.е.

D(CX) = C²*D(X)

3. Доказать свойство дисперсии: D(X -Y) = D(X) + D(Y)

Теорема:

Если случайные величины Х и У независимы, то

D(X -Y) = D(X) + D(Y) (1)

Доказательство:

Сначала докажем формулу:

D(X +Y) = D(X) + D(Y) (2)

Из определения дисперсии имеем

D(X + Y) = М(Х + У - М(Х + У))²

Применяя свойство суммируемости математического ожидания, получаем

D(X + Y) = М(Х + У - М(Х) – М(У))² = М((Х - М(Х)) + (У - М(У))² =

= М((Х - М(Х))² + 2* (Х - М(Х))*( У - М(У)) + (У - М(У))²) =

= М((Х - М(Х))² + М(2*(Х – М(Х))*(У – М(У))) + М(У-М(У))² =

= D(X) + D(Y) + M(2*(X – M(X))*(Y- M(Y)). (3)

Осталось установить, что

M(2*(X – M(X))*(Y- M(Y))= 0.

Из независимости случайных величин Х и У следует независимость случайных величин:

(Х –М(Х)) и (У – М(У)).

Тогда, в силу свойства математического ожидания, для независимых величин получаем

М(2*(Х – М(Х))*(У – М(У))= 2*М (Х - М(Х))*( У - М(У))=

= 2* (М(Х) - М(Х))*( М(У) - М(У))=2*0*0 = 0

Отсюда и из формулы (3) получаем

D(X +Y) = D(X) + D(Y)

Из последней формулы следует

D(X -Y) = D(X+(-Y))=D(X)+D(-Y)=D(X)+(-1)²*D(Y) = D(X) + D(Y).

4. Теорема сложения вероятностей несовместных случайных событий.

Определение. Два события А и Б называются несовместными, если их совместное наступление невозможно, т.е. нет такого исхода случайного эксперемента одновременно принадлежащего событию А и собитию Б.

Для несовместных событий: А*Б=Ø, вероятность совместного наступления Р(А*Б)=0.

Теорема. Для двух несовместных событий А и Б (А*Б=Ø), вероятность события наступления хотя бы одного из них (А+Б), вычесляется по формуле:

Р(А+Б)=Р(А)+Р(Б)

Доказательство. Эту формулу можно вывести из формулы теоремы сложения двух совместных событий:

Р(А+Б)=Р(А)+Р(Б)-Р(А*Б)

Учитывая, что Р(А*Б)=0 для несовместных событий, отсюда получаем утверждение теоремы.

Замечание 1. Утверждением теоремы является содержание аксиома 3 теории вероятности, т.е. доказательство не требуется.

Замечание 2. Если события А1, А2,…, Аn несовместны, т.е. Аi*A= Ø для любых i≠j, то Р(А1+А2+…+Аn) = Р(А1+А2+…+Аn)