Основные характеристики параметров генеральной и выборочной совокупности

В основе статистических выводов проведенного исследования лежит распределение случайной величины  , наблюдаемые же значения (х₁, х₂, … , х_n) называются реализациями случайной величины Х (n — объем выборки). Распределение случайной величины  в генеральной совокупности носит теоретический, идеальный характер, а ее выборочный аналог является эмпирическим распределением. Некоторые теоретические распределения заданы аналитически, т.е. их параметры определяют значение функции распределения   в каждой точке пространства возможных значений случайной величины  . Для выборки же функцию распределения определить трудно, а иногда невозможно, поэтому параметры оценивают по эмпирическим данным, а затем их подставляют в аналитическое выражение, описывающее теоретическое распределение. При этом предположение (или гипотеза) о виде распределения может быть как статистически верным, так и ошибочным. Но в любом случае восстановленное по выборке эмпирическое распределение лишь грубо характеризует истинное. Важнейшими параметрами распределений являются математическое ожидание   и дисперсия  .

По своей природе распределения бывают непрерывными и дискретными. Наиболее известным непрерывным распределением является нормальное. Выборочными аналогами параметров   и для него являются: среднее значение   и эмпирическая дисперсия  . Среди дискретных в социально-экономических исследованиях наиболее часто применяетсяальтернативное (дихотомическое) распределение. Параметр математического ожидания  этого распределения выражает относительную величину (или долю) единиц совокупности, которые обладают изучаемым признаком   (она обозначена буквой  ); доля совокупности, не обладающая этим признаком, обозначается буквой q (q = 1 — p). Дисперсия же   альтернативного распределения также имеет эмпирический аналог  .

В зависимости от вида распределения и от способа отбора единиц совокупности по-разному вычисляются характеристики параметров распределения. Основные из них для теоретического и эмпирического распределений приведены в табл. 9.1.

Долей выборки k_n называется отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

k_n = n/N.

Выборочная доля w — это отношение единиц, обладающих изучаемым признаком x к объему выборки n:

w = n_n/n.

Пример. В партии товара, содержащей 1000 ед., при 5% выборке доля выборки k_n в абсолютной величине составляет 50 ед. (n = N*0,05); если же в этой выборке обнаружено 2 бракованных изделия, то выборочная доля брака w составит 0,04 (w = 2/50 = 0,04 или 4%).

Так как выборочная совокупность отлична от генеральной, то возникают ошибки выборки.

Оценка параметров генеральной совокупности

Характеристики положения

Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение s. Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной.

Точечной оценкой генеральной средней является выборочное среднее  .

Выборочным средним называется среднее арифметическое значение признака выборочной совокупности.

Если все значения x₁, x₂,..., x_n признака выборки различны (или если данные не сгруппированы), то:

Если же все значения признака x₁, x₂,..., x_n имеют соответственно частоты n₁, n₂,..., n_k, причем n₁ + n₂ +...+ n_k = n (или если выборочное среднее вычисляется по вариационному ряду), то

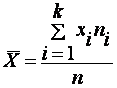
В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего   значениями вариант считают середины интервалов.

Выборочное среднее является основной характеристикой положения, показывает центр распределения совокупности, позволяет охарактеризовать исследуемую совокупность одним числом, проследить тенденцию развития, сравнить различные совокупности (выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0).

Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения.

Дисперсия выборки или выборочная дисперсия (от английского variance) – это мера изменчивости переменной. Термин впервые введен Фишером в 1918 году.

Выборочной дисперсией D_в называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения  .

Если все значения x₁, x₂,..., x_n признака выборки объема n различны, то:

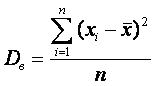
Если же все значения признака x₁, x₂,..., x_n имеют соответственно частоты n₁, n₂,..., n_k, причем n₁ + n₂ +...+ n_k = n, то

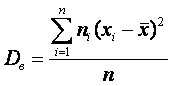
Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.

Среднее квадратическое отклонение (стандартное отклонение), (от английского standard deviation) вычисляется как корень квадратный из дисперсии.

Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.

Непараметрическими характеристиками положения являются мода и медиана.

Модой M_o называется варианта, имеющая наибольшую частоту или относительную частоту.

Медианой M_e называется варианта, которая делит вариационный ряд на две части, равные по числу вариант.

При нечетном числе вариант (n=2k+1)

M_e = x_k+1,

а при четном числе вариант (n=2k)

M_e = (x_k + x_k+1)/2.