Билет № 12

1. Случайные величины. Числовые характеристики дискретных и непрерывных случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение.

См.учебник Морозов стр.114-125

Часто в результате испытания происходят события, заключающиеся в том, что некоторая величина принимает одно из своих возможных значений.      В таких случаях удобно вместо множества событий рассматривать одну переменную величину (называемую случайной величиной). Случайная величина обозначается через X, Y, Z, … и т.д.      Случайной называется величина, которая в результате испытания может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.      Пример. В студенческой группе 25 человек. Пусть величина Х – число студентов, находящихся в аудитории перед началом занятий. Ее возможными значениями будут числа 0, 1, 2,…,25.      При каждом испытании (начало занятий) величина Х обязательно примет одно из своих возможных значений, т.е. наступит одно из событий Х = 0, Х = 1, …, Х = 25.      Пример. Измерение курса акции некоторого предприятия. Возможные события заключаются в том, что стоимость акции Y примет некоторое значение в пределах от 0 до ∞.      Пример. Однократное бросание игральной кости. Возможные события заключаются в том, что на верхней грани выпадает Z: 1, 2, 3, 4, 5, 6.      Пример. Подбрасывается монета n раз. Возможные результаты: герб выпал 0, 1, 2, …, n раз.      Различают дискретные и непрерывные случайные величины.      Если множество возможных значений случайной величины конечно или образуют бесконечную числовую последовательность, то такая случайная величина называется дискретной (примеры 3.1, 3.3, 3.4).      Случайная величина, множество значений которой заполняет сплошь некоторый числовой промежуток, называется непрерывной (пример 3.2). Заметим, что дискретные и непрерывные величины не исчерпывают все типы случайных величин.      Если случайная величина не относится ни к дискретным, ни к непрерывным случайным величинам, то ее называютсмешанной.      Очевидно, что для полной характеристики дискретной случайной величины мало знать ее значения. Необходимо им поставить в соответствие вероятности.      Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины. называется многоугольником (полигоном) распределения. Каждая случайная величина полностью определяется своей функцией распределения.

В то же время при решении практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся в первую очередь математическое ожидание и дисперсия.

 Математическое ожидание случайной величины

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .

Математическое ожидание дискретной случайной величины x , имеющей распределение

 

x1	x2	...	xn
p1	p2	...	pn

называется величина  , если число значений случайной величины конечно.

Если число значений случайной величины счетно, то  . При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Математическое ожидание непрерывной случайной величины с плотностью вероятностей p_x(x) вычисляется по формуле  .

Основные свойства математического ожидания:

• математическое ожидание константы равно этой константе, Mc=c ;

• математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и bсправедливо: M(ax + bh ) = a M(x )+ b M(h );

• математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).

 Дисперсия случайной величины

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x - Mx )².

Легко показать, что Dx = M(x - Mx )²= Mx ² - M(x )².

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx ² >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

,  .

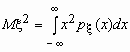Для определения меры разброса значений случайной величины часто используется среднеквадратичное отклонение  , связанное с дисперсией соотношением  .

Основные свойства дисперсии:

• дисперсия любой случайной величины неотрицательна, Dx 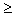  0;

• дисперсия константы равна нулю, Dc=0;

• для произвольной константы D(cx ) = c²D(x );

• дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x ±h ) = D(x ) + D (h ).