1.3. Выбор оптимального варианта компоновки редуктора

1.3.1. Идентификаторы программы REDUCE. Чтение распечатки

В процессе работы программы REDUCE по данным введенным по табл. 1.1 численным значениям параметров присваиваются идентификаторы, приведенные ниже. В верхней части содержатся исходные данные для расчетов, записанные в три строки и несколько столбцов. Показаны:

• обозначение группы, фамилия студента, обозначение схемы редуктора;

• MOM – момент на колесе тихоходной передачи T_2Т, Нм;

• I – передаточное отношение редуктора, i;

• SIG1 и SIG2 – предварительно назначенные значения допускаемых контактных напряжений для быстроходной и тихоходной передач редуктора, соответственно, [_H]_Б и [_H]_Т, МПа;

• PSI1 и PSI2 – коэффициенты ширины зубчатых колес для быстроходной и тихоходной передач, соответственно, _ba Б и _ba Т ;

• L1 и L2 – коды зубчатых быстроходной и тихоходной передач (напоминаем: 1 – прямозубая, 2 – косозубая, 3 – шевронная передача);

• CH – частота вращения быстроходного вала редуктора мин^-1, обозначаемое как n;

• TE – эквивалентное время работы L_he , час.

Ниже представлены варианты расчетов, сгруппированные в файлы, содержащие:

 строки идентификаторов, в которых:

• AW – межосевые расстояния передач a_w Б и a_w Т, мм;

• B – ширина венца зубчатого колеса быстроходной и тихоходной передач, b_w Б и b_w Т, мм. Внимание! Для шевронных передач указана суммарная ширина колес двух полушевронов;

• Z1 и Z2 – числа зубьев шестерни z₁ и колеса z₂ соответствующей передачи;

• U – передаточное число зубчатой пары для быстроходной u_Б и тихоходной u_Т передач;

• MOD – модуль зацепления (мм) для обеих передач, m_Б и m_Т;

• D1 и D2 – начальные (или делительные) диаметры шестерен и колес, d₁, d₂ или d_w1 и d_w2 (мм) – соответственно уточняются при наличии в распечатке коэффициентов смещения X, отличных от нуля;

• X – суммарные коэффициенты смещения для обеих передач;

• BETA – углы наклона зубьев (град) на делительном диаметре шестерни и колеса, _Б и _Т .

Ниже приведены значения требуемой динамической грузоподъемности C, кН для подшипников валов редуктора в двух колонках: левая содержит значения C для шариковых радиальных, правая – для конических радиально-упорных подшипников:

– ВАЛ1 – быстроходного вала;

– ВАЛ2 – промежуточного вала;

– ВАЛ3 – тихоходного вала.

1.3.2. Обработка результатов расчета на ПЭВМ. Оптимизация по критериям минимального объема и массы зубчатых колес

Для редукторов, выполненных по развернутой схеме (схема 20, 21 и 22) вид зубчатых передач изображают в двух проекциях.

На рис. 1.1. приведены основные размеры зубчатых передач редуктора по схеме 21 с шевронной быстроходной передачей и выделены размеры A, B и L, определяемые для каждого из содержащихся в распечатке варианта по следующим формулам:

A = d_a2 max ;

B = b_w Б + b_w Т + 3a;

L = 0,5(d_a2 Б + d_a2 Т) + a_w Б + a_w Т + (3…4)a;

b₀ = (3…4)a,

где d_a2 max – наибольшая из двух величин d_a2 Б или d_a2 Т; a – зазор между корпусом и вращающимися деталями передач (колесами) (мм), определяемый по формул:

.

Для других схем (схемы 20 и 22) эскиз по рис. 1.1 выполняется аналогично, однако, для схемы 24 принято соосное расположение быстроходного и тихоходного валов и изображение принимает другой вид, приведенный на рис. 1.2.

В этом случае, размеры, определяющие габаритно-массовые характеристики, находим по формулам:

A = d_a2 max ;

B = b_w Б + b_w Т + 2a + (0,45…0,55)a_w;

L = a_w + 0,5(d_a2 Б + d_a2 Т).

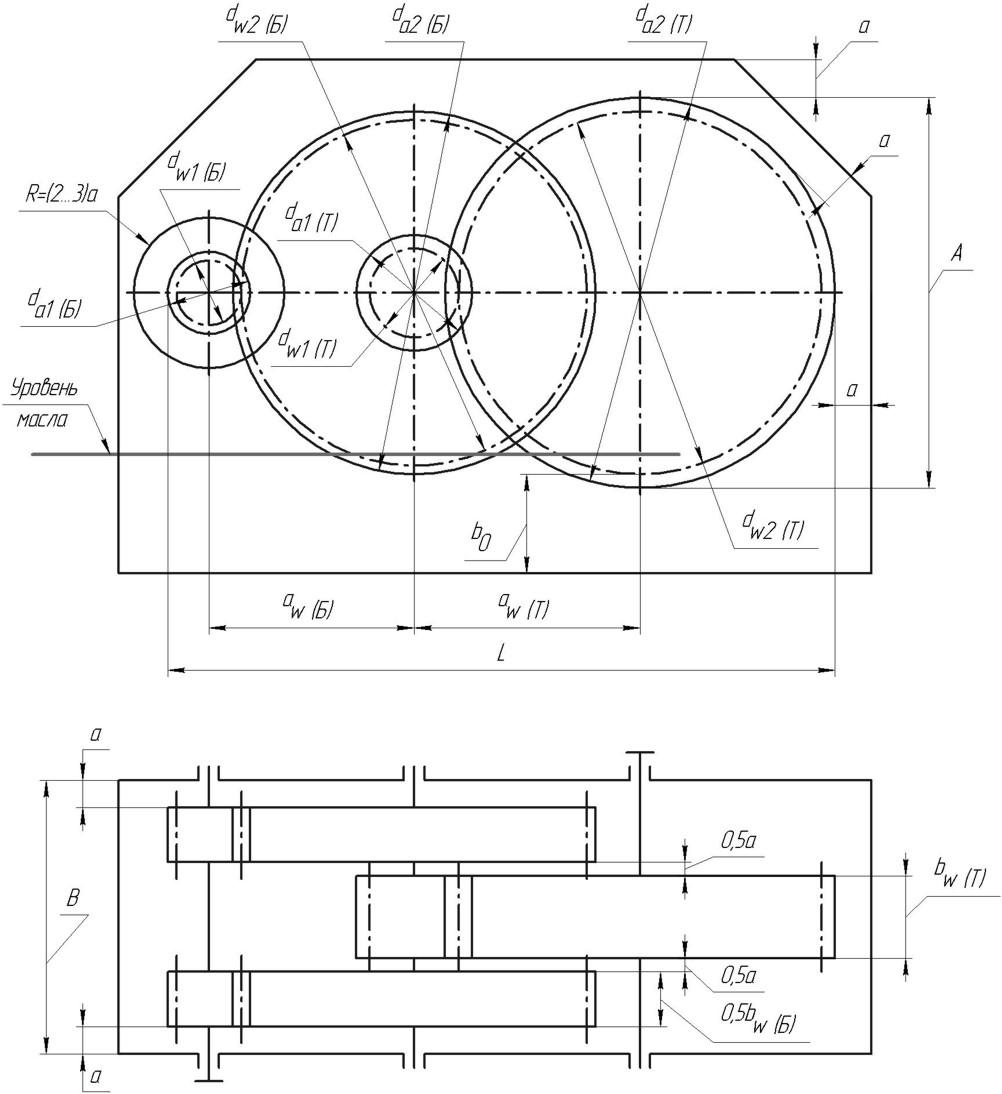
Рис. 1.1

Из условия оптимизации коэффициента перекрытия _  1,1… …1,2 ширину колеса быстроходной ступени b_w Б необходимо предварительно уточнить по формуле:

b_w Б = _m / sin.

Сравнение вариантов рекомендуется производить по диаграмме, которая строится в следующем порядке.

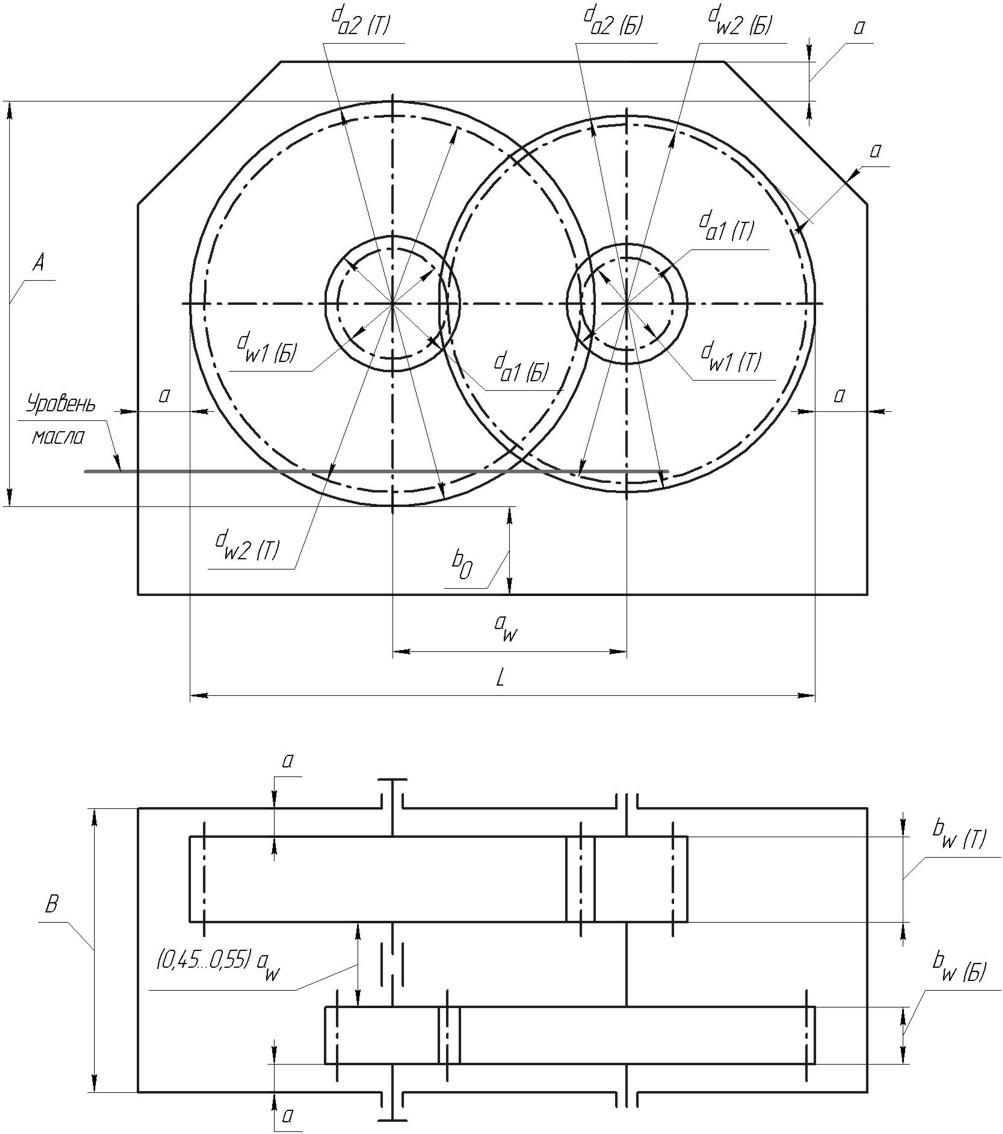
Рис. 1.2.

Объем корпуса редуктора, определяющий массу редуктора, можно оценить по формуле:

V = ABL.

Массу заготовок для зубчатых колес, характеризующую затраты на материалы, вычисляется по формуле:

.

где – коэффициент пропорциональности, для стальных зубчатых колес можно принять равным 6,12, кг/дм³. Если при расчетах V и m размеры колес выражать в дм, тогда объем выразится в литрах, а масса в кг.

Диаграмма, показывающая изменение массы и объема в зависимости от рассматриваемого варианта, представлена на рис. 1.3.

Рис. 1.3.

1.3.3. Оценка условий смазки и выбор способа смазки передач редуктора

Двухступенчатые редукторы обычно смазываются картерным способом, при этом в корпус редуктора заливается масло, которое при эксплуатации привода периодически заменяется. Такой способ рекомендуется при окружных скоростях колес до 5 м/с и контактных напряжениях _H  1000 МПа. Большинство проектируемых студентами редукторов соответствует этим условиям.

Выбранный вариант должен отвечать условию смазки зубчатых колес передач редуктора. Оптимальным считается случай, когда колесо быстроходной передачи редуктора при окружной скорости V_окр = 0,3…12,5 м/с погружено в масляную ванну на глубину (2… …2,5)m. При этом колесо тихоходной передачи погружается в масло не более, чем на 0,3d_a2 Т . Считают, однако, что при окружной скорости V_{окр Т}  1 м/с в масло можно погружать только тихоходное колесо, при этом смазка быстроходной передачи и подшипников надежно обеспечивается за счет разбрызгивания масла.

В редукторах, выполненных по соосной схеме, в масло погружают оба зубчатых колеса приблизительно на одинаковую глубину.

На рис. 1.1 и 1.2 отмечен уровень масла, отвечающий вышеприведенным требованиям, если объем масла V_м в корпусе не противоречит условию

V_м = (0,25…0,5)Р, (л)

1.3.4. Графическое оформление результатов по оптимальному варианту. Первый этап компоновки

Изображение, соответствующее первому этапу компоновки, вычерчивается на миллиметровой бумаге в масштабе 1:1. Желательно каждую проекцию представить на отдельном листе формата А1 с учетом дальнейшей проработки конструкции редуктора.

1.3.5. Геометрический расчет передач редуктора

Геометрический расчет выполняется в минимальном объеме. Определению подлежат: делительные d₁ и d₂ и начальные d_w1 и d_w2 диаметры колес; коэффициенты смещения X₁ и X₂; диаметры окружностей вершин d_a1 и d_a2; угол зацепления _w; коэффициент торцевого перекрытия _; коэффициент осевого перекрытия _ для косозубых колес. Все колеса нарезаются реечным инструментом или долбяком с исходным контуром по ГОСТ 13755-81 с параметрами: угол профиля  = 20; коэффициентом головки (ножки) зуба ; коэффициент радиального зазора с^* = 0,25.

1.3.5.1. Прямозубые передачи

Коэффициенты смещения колес определяем по блокирующим контурам [9], используя линию 15 – линию выровненных удельных скольжений. Суммарный коэффициент смещения X = X₁ + X₂ = X_ задан в распечатке. Далее:

– угол зацепления

;

– делительные диаметры приводятся в распечатке. Тем не менее:

– диаметры вершин:

– диаметры впадин:

– начальные диаметры:

– коэффициент перекрытия:

где – для каждого из колес.

1.3.6.2. Косозубые передачи

Расчет основных размеров проводят по формулам п. 1.3.6.1., за исключением диаметров d₁ и d₂ . Принимают:

Далее размеры d_a1 , d_a2 , d_f1 и d_f2 вычисляют в функции делительных диаметров d₁ и d₂.

Коэффициент торцового перекрытия для косозубых передач:

.

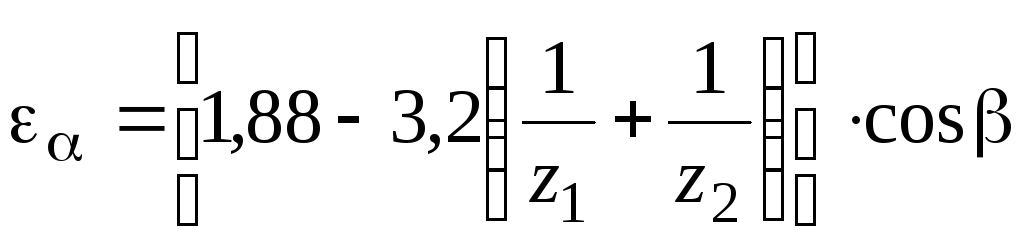Коэффициент осевого перекрытия:

.

Суммарный коэффициент перекрытия:

.