
- •Глава 2. Дифференциальное исчисление функций нескольких переменных
- •§1.Понятие функции нескольких переменных
- •§2.Предел и непрерывность функции нескольких переменных
- •2.1. Предел функции нескольких переменных
- •2.2. Непрерывность функции нескольких переменных
- •§3. Дифференцируемость функции нескольких переменных
- •3.1. Частные производные (ч.Пр.) функции двух переменных
- •Механический смысл частных производных
- •Геометрический смысл частных производных функции 2-х переменных
- •3.2. Понятие о дифференцирумости функции 2-х переменных
- •3.3. Дифференциал функции нескольких переменных. Приложение к приближенным вычислениям
- •3.4.Касательная плоскость к графику функции двух пременых Геометрический смысл дифференциала функции двух переменных
- •§4. Сложная функция и ее дифференцируемость
- •4.1. Понятие вектор-функции и композиции функций
- •4.2. Дифференцируемость сложной функции
- •Из дифференцируемости функции в точке м0 следует , что ее приращение
- •Где , 0, еслиX, у0.
- •4.3.Инвариантность формы дифференциала
- •§5. Производная по направлению. Градиент
- •§6. Неявные функции
- •§7.Частные производные и дифференциалы высших порядков
- •§8. Формула Тейлора для функции двух переменных
- •§9. Экстремумы функции двух переменных
- •9.1. Локальный экстремум
- •9.2. Абсолютный экстремум
- •9.3. Условный экстремум
- •Глава 3. Интегральное исчисление функций нескольких переменных §1. Двойной интеграл и его свойства.
- •1.1. Понятие двойного интеграла
- •1.2. Свойства двойного интеграла
- •1.3. Вычисление площадей фигур и объемов тел с помощью двойных интегралов
- •§2. Вычисление двойных интегралов
- •Пример 2.3. Поменять порядок интегрирования в интеграле §3. Замена переменных в двойном интеграле
- •§4.Площадь гладкой поверхности
- •§5. Тройной интеграл и его свойства
- •5.1. Определение тройного интеграла и его свойства
- •Свойства тройного интеграла
- •Геометрический смысл тройного интеграла
- •5.2. Вычисление тройного интеграла
- •§6. Замена переменных в тройном интеграле
- •Цилиндрические координаты
- •Сферические координаты
- •Глава 4. Криволинейные интегралы
- •1.1. Понятие криволинейного интеграла
- •1.2. Свойства криволинейного интеграла
- •1.3. Существование и вычисление криволинейного интеграла
- •§2. Формула Остроградского – Грина
- •Формула (2.3), связывающая криволинейный интеграл с двойным, называется формулой Остроградского – Грина.
- •§3 .Условие независимости криволинейного интеграла от пути интегрирования
- •§4. Восстановление функции по ее полному дифференциалу
- •1 Способ
§6. Неявные функции
Рассмотрим уравнение F(x,y) = 0 (6.1), где F – функция двух переменных, которая определена в прямоугольной области D = [a, b; c,d].
Пусть
для любого х
[a,b]
это уравнение имеет решение относительно
у.
Тем самым каждому х
[a,b]
ставится в соответствие определенное
число у
– решение уравнения(6.1) (заметим, что
уравнение (6.1) может иметь несколько
решений относительно у,
но мы выбираем какое-то одно из них). Это
означает , что на множестве [a,b]
определена функция y
= f(x).
При этом правило f,
ставящее
в соответствие каждому х
некоторое число у,
не указано здесь явно, а задано с
помощью уравнения (6.1).
Такой способ задания функции y
= f(x)
называется неявным, а сама функция
неявной. Основное свойство неявной
функции y
= f(x)
заключается в правдивости равенства
![]()
Определение
6.1. Если
функция двух переменных F(x,y)
определена в некоторой области D
![]() и существует такая функция f
одной переменной, определенная на
некотором подмножестве Х числовой
прямой, что для любого
х
Х
имеет место включение
и существует такая функция f
одной переменной, определенная на
некотором подмножестве Х числовой
прямой, что для любого
х
Х
имеет место включение
![]()
D
и выполняется равенство
D
и выполняется равенство
![]() ,
то функция f
называется неявной
функцией, определенной уравнением
F(x,y)
= 0.
Говорят также, что функция f
задана
неявно уравнением (6.1).
,
то функция f
называется неявной
функцией, определенной уравнением
F(x,y)
= 0.
Говорят также, что функция f
задана
неявно уравнением (6.1).
Пример
6.1. Уравнение
![]() определяет неявную функцию
определяет неявную функцию
![]() на множестве R.
на множестве R.
Пример
6.2.
Уравнение
![]() не определяет неявную функцию на
не определяет неявную функцию на
[-1,1],
т.к. каждому
![]() соответствует два значения
соответствует два значения
![]() Однако, потребовав сужение этого
соответствия
Однако, потребовав сужение этого
соответствия
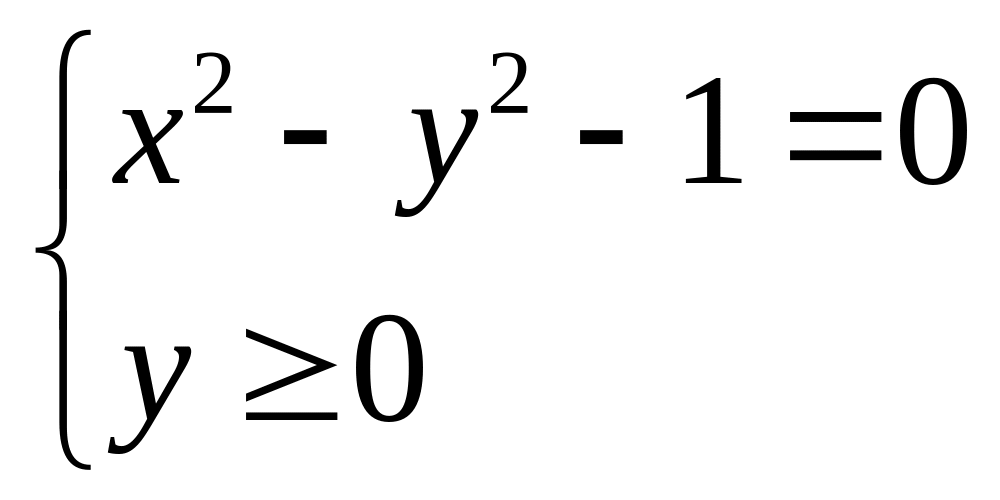 ,
получим, что рассматриваемое уравнение
определяет неявную функцию со значениями
,
получим, что рассматриваемое уравнение
определяет неявную функцию со значениями
![]() на
отрезке [-1,1].
на
отрезке [-1,1].
Теорема
6.1 (о
существовании неявной функции).
Пусть
дано уравнение (6.1) и функция
![]() удовлетворяет
следующим условиям:
удовлетворяет
следующим условиям:
1)определена
и непрерывная вместе со своими частными
производными
![]() в некоторой окрестности точки
в некоторой окрестности точки
![]()
2)![]()
3)![]()
тогда имеют место следующие утверждения:
в
некоторой
- окрестности точки х0
уравнение
(6.1) определяет неявную функцию
![]()
она дифференцируема в этой окрестности и ее производную можно вычислить по формуле

Теорему примем без док-ва.
Пример
6.3. Определяет
ли уравнение
![]() (6.3) неявную функцию в окрестности точки
х
= 0
?
(6.3) неявную функцию в окрестности точки
х
= 0
?
Рассмотрим точку
М0(0,1).
Функция
непрерывна
в некоторой
-окрестности этой точки как элементарная;
![]() производные
производные
![]() также непрерывные в этой окрестности;
также непрерывные в этой окрестности;
![]()
Таким
образом, согласно теореме 6.1, уравнение
(6.3) определяет в некоторой
-окрестности точки М0
непрерывную, дифференцируемую неявную
функцию
![]() ,
производную которой можно найти по
формуле (6.2):
,
производную которой можно найти по
формуле (6.2):
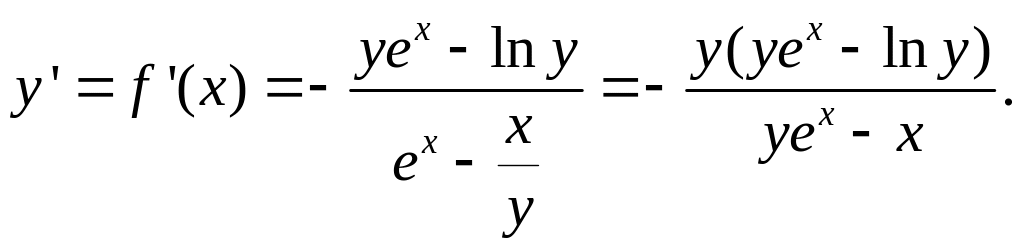
Замечание. Аналогично вводится понятие неявной функции n – переменных.
Пусть
дано уравнение F(x,y)
= 0 (6.4), где
![]() Функция z
= F(x,y)
– функция n
+ 1 переменной,
тогда решение уравнения (6.4) можно
представить в виде соответствия
Функция z
= F(x,y)
– функция n
+ 1 переменной,
тогда решение уравнения (6.4) можно
представить в виде соответствия
![]() ,
где
,
где
![]() ,
,
![]() Если в этом соответствии каждому
соответствует
единственное значение
,
то говорят, что уравнение (6.4) определяет
неявную функцию y
= f(x),
где
,
которая обращает уравнение (6.4) в тождество
Если в этом соответствии каждому
соответствует
единственное значение
,
то говорят, что уравнение (6.4) определяет
неявную функцию y
= f(x),
где
,
которая обращает уравнение (6.4) в тождество
![]()
![]()
Теорема
6.2. Пусть
дано уравнение (6.4), где
![]() ,
функция
удовлетворяет
следующим условиям:
,
функция
удовлетворяет
следующим условиям:
1)определена
и непрерывна вместе со своими частными
производными
![]() в некоторой окрестности
точки
в некоторой окрестности
точки
![]()
![]() ;
;
2)
3)![]()
тогда имеют место следующие утверждения:
в
некоторой
- окрестности точки х0Rn
уравнение
(6.4)
определяет единственную неявную функцию
![]()
она дифференцируема в этой окрестности;
частные производные ее находятся по формуле
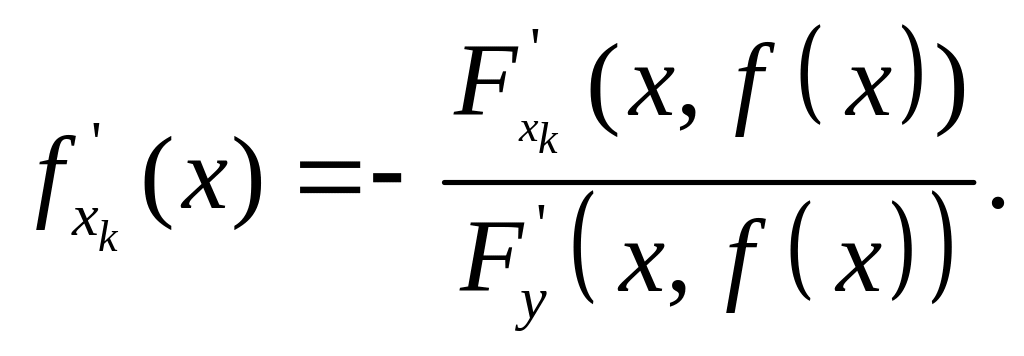 (6.5)
(6.5)
Пример
6.4. Найти
![]() функции
,
заданной уравнением
функции
,
заданной уравнением
![]() .
.
Напомним
уравнение касательной плоскости к
графику функции
в точке
![]() и нормали
и нормали
![]()
Если уравнение поверхности задано в неявном виде формулой F(x,y,z) = 0, то уравнение касательной плоскости и нормали имеют вид соответственно:
![]() ;
;
![]()
