1.3. Существование и вычисление криволинейного интеграла

Пусть кривая задана параметрически уравнениями

t [,] , где параметру  соответствует точка А, - точка В, функции  и  - непрерывно дифференцируемые на [,]. Пусть на кривой определены непрерывные функции P(x,y) и Q(x,y). Тогда криволинейный интеграл существует и вычисляется по формуле:

=

_{Если кривая АВ является графиком непрерывно дифференцируемой на отрезке [a,b] функции y=f(x), то криволинейный интеграл вычисляется переходом к определенному интегралу:}

=

_{Пример 1.1. Вычислить криволинейный интеграл:}

_{Пример1.2. Вычислить криволинейный интеграл}

_{, где АВ- верхняя половина эллипса , которую проходят в положительном направлении.}

§2. Формула Остроградского – Грина

Это формула устанавливает связь между криволинейным интегралом по замкнутому контуру С и двойным интегралом по области, ограниченной этим контуром.

Пусть D – область первого типа, ограниченная замкнутой кривой  = ABCDA: прямыми x = a, x = b, графиками функций y = f₁(x), y = f₂(x) (f₁(x)< f₂(x) x[a,b]). Пусть в этой области D определена функция P(x,y) , непрерывная вместе со своей частной производной . Рассмотрим двойной интеграл по области D:

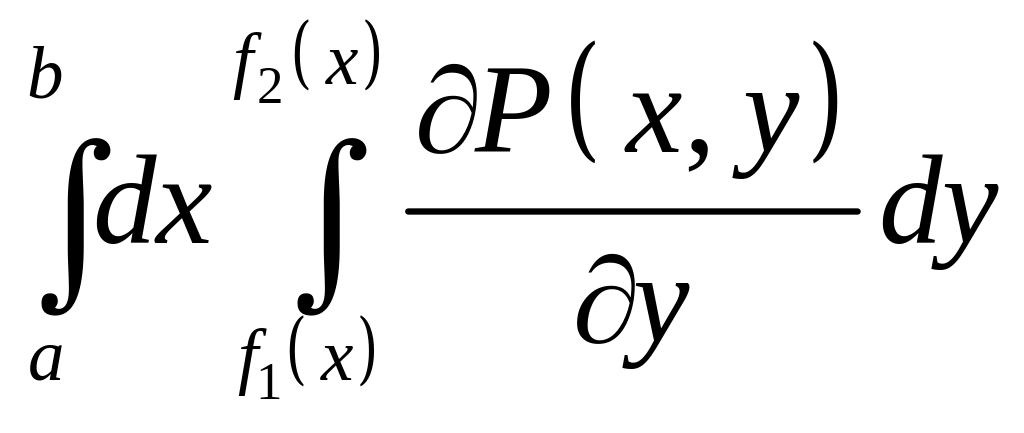= = = - =[1-й интеграл–криволинейный интеграл функции Р по кривой DC, второй – криволинейный интеграл функции Р по кривой АВ] = - =[т.к , , ] = - - - - = - = - = , где  = ABCDA – замкнутая кривая, ограничивающая область D. Таким образом получили формулу = - . (2.1)

Самостоятельно рассмотреть случай, когда область D – область 2-го типа и на ней определена функция Q(x,y), непрерывная вместе со своей частной производной . Получить формулу

. (2.2)

Определение 2.1. Область D называется простой областью, если ее можно разбить на конечное число областей первого типа и независимо от этого на конечное число областей второго типа.

Теорема 2.1. Пусть в простой области заданы функции P(x,y) и Q(x,y), непрерывные вместе со своими частными производными и Тогда имеет место формула

= . (2.3)

где С – замкнутый контур области D.

Формула (2.3), связывающая криволинейный интеграл с двойным, называется формулой Остроградского – Грина.

 Т.к. область D простая, то, если разбить ее на конечное число областей 1 типа, то получим формулу (2.1), а если на конечное число областей 2-го типа, то формулу (2.2). Если сложить обе формулы, то получим формулу (2.3). 

Пример2.1. С помощью формулы Остроградского – Грина вычислить

, где  - окружность которую проходят в положительном направлении.

§3 .Условие независимости криволинейного интеграла от пути интегрирования

Определение 3.1. Говорят, что замкнутая квадрируемая область D односвязна, если любую замкнутую кривую l D можно непрерывно деформировать в точку так, чтобы все точки деформируемой кривой принадлежали этой области D (область без “дырок” – D₁), если такая операция не выполнима, то область называется многосвязной (с “дырками” – D₂).

Определение 3.2. Если значение криволинейного интеграла по кривой АВ не зависит от вида кривой, соединяющей точки А и В, то говорят, что этот криволинейный интеграл не зависит от пути интегрирования:

.

Теорема 3.1. (о независимости крив. интеграла от пути интегрирования) Пусть в замкнутой квадрируемой односвязной области D определены непрерывные вместе со своими частными производными функции P(x,y) и Q(x,y). Тогда следующие 4 условия равносильны (эквивалентны):

1) криволинейный интеграл по замкнутому контуру

= 0 (3.1),

где С – любой замкнутый контур в D;

2) криволинейный интеграл не зависит от пути интегрирования в области D, т.е. (3.2);

3) дифференциальная форма P(x,y)dx + Q(x,y)dy является полным дифференциалом некоторай функции F в области D, т.е. что существует такая функция F, что (х,у)  D будет иметь место равенство

dF(x,y) = P(x,y)dx + Q(x,y)dy; (3.3)

4) для всех точек (х,у)  D будет выполняться следующее условие:

= (3.4)

докажем по схеме .

Докажем, что из .

Пусть дано условие (3.1), т.е. = 0  по свойству (2) = 0   по свойству(1)  .

Докажем, что из .

Дано, что крив.интегррал не зависит от пути интегрирования, а только от выбора начала и конца пути 

₌ .

Рассмотрим функцию F(x,y) =

Пакажем, что дифференциальная форма P(x,y)dx + Q(x,y)dy является полным дифференциалом функции F(x,y), т.е.

P(x,y) = (3.5 ), G(x,y)= (3.6).

Дадим приращение _хF (x,y)= F( х + х,у) –F (x,y)=

= = _{, где x<c<x+x. Тогда}

=P(x,y) (в силу непрерывности функции Р). Получили формулу (3.5). Аналогично получается формула (3.6). Таким образом, доказали: если выполняется 2, то дифференциальная форма является полным дифференциалом функции

F(x,y) =

_{Для которой выполняется равенство (3.3).}

Докажем, что из .

Дано dF(x,y) = P(x,y)dx + Q(x,y)dy.

Ясно, что = Р(х,у). Тогда (3.7)

Аналогично =Q(x,y) . (3.8)

Т.к. по условию теоремы правые части равенств (3.7) и (3.8) непрерывные функции, то и левые части этих равенств непрерывные функции по теореме о равенстве смешанных производных левые части будут равны , а значит и

= .

Докажем, что из 41.

Выберем любой замкнутый контур С в области D, ограничивающий область D₁.

Функции P и Q удовлетворяют условию теоремы Остроградского-Грина:

= . (3.9)

В силу равенства (3.4) в левой части (3.9) интеграл равен 0, а значит и правая часть равенства равна 0  = 0. 

Замечание 3.1. Теорема 3.1. может быть сформулирована в виде трех самостоятельных теорем:

Теорема 3.1*. Для того, чтобы в односвязной квадрируемой области D крив.интеграл не зависел от пути интегрирования  чтобы выполнялось условие (3.1), т.е.

= 0  С  D.

Теорема 3.2*. Для того, чтобы в односвязной квадрируемой области D крив.интеграл не зависел от пути интегрирования  чтобы выполнялось условие (3.3): дифференциальная форма P(x,y)dx + Q(x,y)dy является полным дифференциалом некоторой функции F в области D.

Теорема 3.3*. Для того, чтобы в односвязной квадрируемой области D крив.интеграл не зависел от пути интегрирования  чтобы выполнялось условие (3.3):

= .

Замечание 3.2. В теореме 3.2* область D может быть и многосвязной.