§5. Тройной интеграл и его свойства

5.1. Определение тройного интеграла и его свойства

Пусть R³ ограниченная замкнутая кубируемая область, на которой определена функция , а Т – разбиение области Е на частичные кубируемые области Е_к(k= ) без общих внутренних точек, причем . Диаметром области Е_к называется число , где есть расстояние между точками области Е_к. Величину будем называть диаметром разбиения Т. В каждой области Е_к выберем произвольную точку . Сумма , где -- объем частной области Е_к, называется интегральной суммой функции на области Е. Значение интегральной суммы зависит от разбиения Т области Е на частичные области и от способа выбора точек .

Определение. Число I называется пределом интегральной суммы при , если для любого существует такое число , что при любом Т-разбиении и при любом выборе точек , выполняется неравенство

Определение 5.1.Если существует конечный предел I интегральной суммы при :

то функцию f называют интегрируемой на области Е, а число I – тройным интегралом от функции f по области Е и обозначают или , т.е. .

Также как и для определенного интеграла Римана, двойного интеграла Римана, имеет место необходимое условие интегрируемости: если функция f интегрируема на множестве Е, то она ограничена на Е. Поэтому предел I может существовать только для ограниченной функции. Как и для двойного интеграла, вводится нижняя и верхняя суммы Дарбу и соответствующий критерий интегрируемости функции, при помощи которого нетрудно доказать интегрируемость непрерывной функции: если функция f непрерывна на Е, то она интегрируема на Е. Можно также доказать и более общую теорему.

Теорема 4.1. Если функция f ограничена на множестве Е и непрерывна на Е за исключением только тех точек области, которые имеют нулевой объем, то она интегрируема на Е.

Свойства тройного интеграла

Все свойства двойных интегралов справедливы и для тройных интегралов, поэтому, не приводя доказательств, назовем их.

Тройной интеграл по телу нулевого объема равен нулю.
Если функции f и g интегрируемы на кубируемой области Е, а и произвольные действительные числа, то и функция 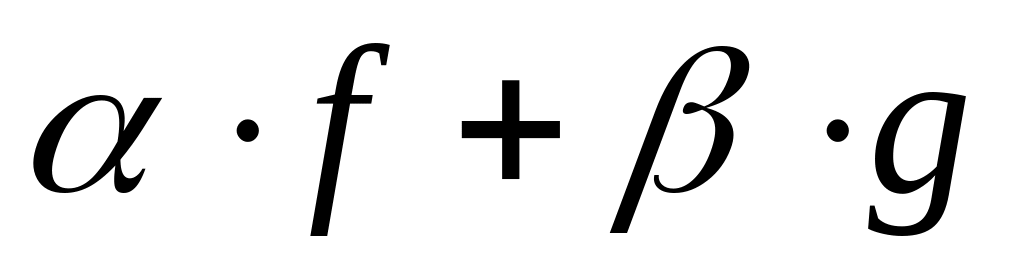интегрируема на Е, причем:

= + + .

Если множества {E_k},(к= ), -- разбиение области Е, то для интегрируемости функции f на Е необходимо и достаточно ее интегрируемость на каждой из областей E_k , причем .