§4. Восстановление функции по ее полному дифференциалу
Если функции P(x,y) и Q(x,y) непрерывные вместе со своими частными производными и в замкнутой , квадрируемой , односвязной области D и
= ,
то,
как следует с теоремы 3.1, дифференциальная
форма
-
полный
дифференциал функции F(x,y),
которую можно найти с помощью криволинейного
интеграла, который не зависит от пути
интегрирования:
1 Способ
Выберем за путь интегрирования ломаную АСВ.
Тогда
F(x,y)=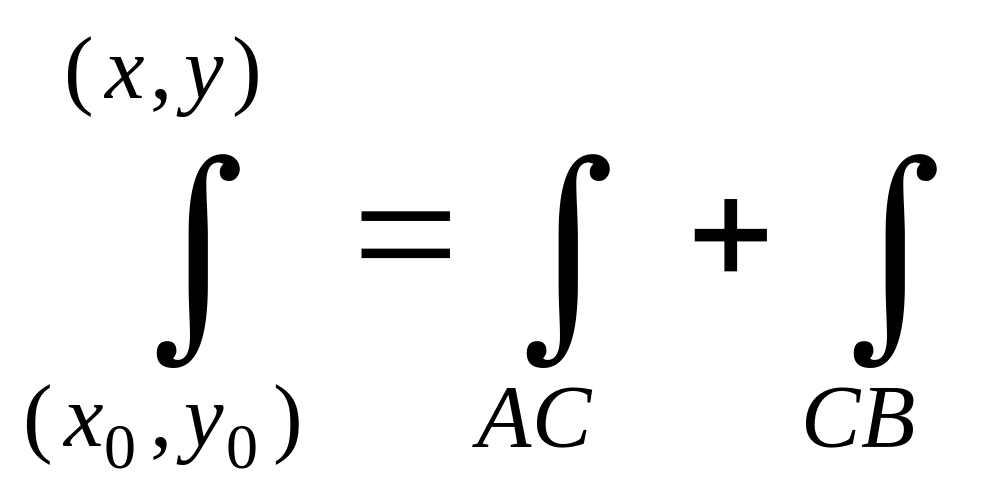
=
=
ІІ способ
Пусть выполняется равенство P(x,y)dx + Q(x,y)dy= dF(x,y).
для функции одной переменной известно , что если
df(x)=
f’(x)dx
, то
f(x)
=
или
f(x)=
. (4.1)
Т.к.
=
Р(х,у),
то в силу (4.1) F(x,y)=
,
(4.2) где (у)
– const,
которая не зависит от х.
Продифференцируем (4.2) по переменной у:
=
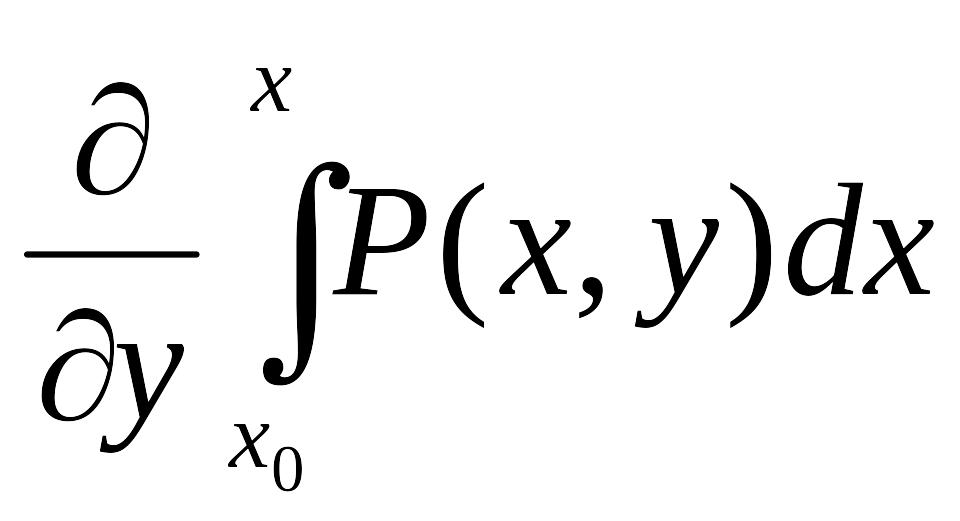+(у), (4.3)
но = Q(x,y) (4.4)
Приравняем правые части равенств (4.3) и (4.4) и найдем
(у )= Q(x,y )- , (4.5)
а затем и (у ) по формуле (4.1). Полученное выражение для (у) подставить в (4.3).