1. Электрические цепи с распределенными параметрами

Если размеры электрической цепи становятся сравнимы с длиной волны, то следует учитывать изменение электромагнитных процессов на участках цепи не только от времени, но и от положения участка в пространстве из-за конечной скорости распространения электромагнитной энергии. Элементы цепи с протяженными размерами называют цепями с распределенными параметрами. К таким цепям, например, можно отнести линию, соединяющую антенну и телевизор – коаксиальный кабель, а так же компьютерные сети. С повышением тактовой частоты и быстродействия соединяющие линии в компьютере (шины данных и т.п.) становятся все ближе к свойствам цепей с распределенными параметрами. Чтобы передать сигнал от одного участка цепи к другому с максимальным КПД, отсутствием отражений и искажений сигнала, связанных с потерей информации, нужно научиться рассчитывать подобные цепи. Впервые с проблемой длинных линий столкнулись в цепях передачи телеграфных сигналов на дальние расстояния. Кирхгоф и Томсон еще до того, как Максвелл сформулировал общие законы электромагнетизма, рассматривали малый элемент линии длиной как элементарный четырехполюсник, структура которого учитывала явления, происходящие в линии, и содержала следующие погонные параметры:  - сопротивление проводов линии (нагрев);    - индуктивность проводов (накопление магнитной энергии);    - емкость между проводниками (накопление электрической энергии);   - проводимость между проводниками (потери в изоляции в виде тепла).     

2. Уравнения линии с распределенными параметрами.

Составим уравнения по законам Кирхгофа для элементарного четырехполюсника:

 

  

 

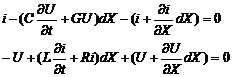
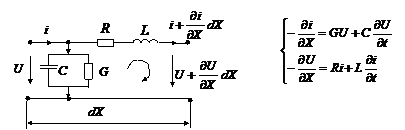
3. Решение уравнений однородной линии при установившемся синусоидальном режиме.

Полученная система уравнений для длинной линии записана в мгновенной форме и годится для расчета линии при любой форме сигнала. В частном случае гармонического сигнала можно, используя символический метод, переписать систему в комплексном виде: .

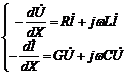Так как временная зависимость в комплексном виде опускается, уравнения записаны в обычных производных. Дифференцируя первое уравнение и подставляя в него второе, получим: , где  - коэффициент распространения в линии;  - коэффициент затухания  (Нп/м);  - коэффициент фазы (рад/м). Решение дифференциального уравнения ищем в виде: . Второе уравнение для нахождения постоянных интегрирования : ,  или , где  - волновое сопротивление линии (Ом).

Схема линии с распределенными параметрами, длиной :

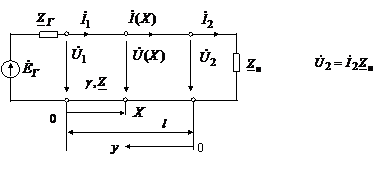
4. Характеристики однородной линии. Условия для неискажающей линии.

Комплексные числа =α+jβ и Z_В в формулах (2 – 9) являются вторичными параметрами однородной линии и называются:  – коэффициент распространения, Z_В – волновое, или характеристическое сопротивление, α – коэффициент затухания, β – коэффициент фазы. Волновое сопротивление Z_В можно определить по формуле(10) через параметры линии на единицу длины (R₀, L₀, G₀, C₀) либо по формуле(10,а) через известные значения входных сопротивлений Z_XX и Z_КЗ, соответственно при холостом ходе и коротком замыкании в конце линии. (10) . (10,а) Коэффициент распространения можно рассчитать по известным первичным параметрам линии (11) либо в соответствии с методикой, изложенной в п.1.2.1 Фазовая скорость волны v_Ф – скорость перемещения волны вдоль линии, понимаемая как скорость перемещения точки, фаза колебания в которой остается постоянной Для воздушных линий фазовая скорость приблизительно равна 3·10⁵ км/с. Длина волны λ – равна расстоянию между двумя точками линии, в которых фазы рассматриваемой величинами различаются на 2π. (13) Линии, физическая длина которых соизмерима с длиной волны считаются длинными линиями.

Условия для неискажающей линии

Вторичные параметры линии  и  зависят от частоты, поэтому чтобы информация при передаче не исказилась, следует выполнить определенные условия: фазовая скорость и коэффициент ослабления всех гармоник должны быть одинаковыми. Тогда все гармоники сигнала придут одновременно в нагрузку, ослабленными в одинаковое число раз, с одинаковым коэффициентом отражения. Для этого необходимо выполнить соотношение: .  Действительно: . .      . 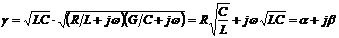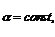Затухание и фазовая скорость не зависят от частоты.