
- •1)Два режима движения жидкости. Опыты Рейнольдса.
- •11) Формула Дарси-Вейсбаха
- •12)Природа коэффициента гидравлического трения λ и основные зависимости для определения его значений
- •25) Вывод формулы Борда (потери напора при внезапном расширении).
- •29)Решение второй задачи расчёта трубопроводов.
- •30)Решение третьей задачи расчёта трубопроводов.
- •35)Истечение жидкости из насадков. Скорость истечения струи
- •36) Расход при истечении реальной жидкости из насадков.
- •37)Гидравлический удар в трубах. Физический механизм появления ударной волны
- •38)Гидравлический удар в трубах. Величина повышения давления при гидравлическом ударе
- •6)Профиль скоростей при ламинарном движении жидкости в круглой трубе.
- •7)Определение максимальной скорости жидкости при движении ламинарного потока в трубе.
- •8)Потери напора при ламинарном режиме движения жидкости (формула Пуазейля)
- •10)Связь между максимальной и средней (расходной) скоростью жидкости при движении потока в трубе.
29)Решение второй задачи расчёта трубопроводов.
Задача 2-ого типа
Дано: |
напор – Н вязкость жидкости – размеры трубопровода – l, d шероховатость стенок – |
Найти – Q |
Порядок решения задачи:
Определяется режим движения путем сравнения напора Н с его критическим значением:
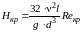 ,
Reкр = 2320.
(9.10)
,
Reкр = 2320.
(9.10)
Если Н Нкр, режим ламинарный, если Н Нкр – турбулентный.
2. Задача решается методом последовательных приближений. В случае ламинарного режима расход определяется из формул (9.4) или (9.7); (9.8') или (9.9'). Однако прямое вычисление здесь затруднено, так как коэффициенты м и являются функцией числа Re. Поэтому в первом приближении определяется из выражения:
 .
(9.11)
.
(9.11)
Далее
определятся расход Q
и средняя скорость
 .
По найденной средней скорости определяется
число Re1. Число
Re1 сравнивается
с Reкр,
если разность между Reкр
и вновь рассчитанным Re1
оказывается
5 %, то расчет считают оконченным.
Если же разность оказывается > 5 %, то
по формуле (9.11) определяется величина
1, где уже
вместо Reкр
подставляют значение Re1.
Далее по одной из формул (9.4) или (9.7);
(9.8') или (9.9') определяют значение Q1,
затем – среднею скорость 1
и далее число Re2.
Затем Re2 сравнивают
с Re1, если разность
5 %, то расчет считают
оконченным. Если же разность оказывается
> 5 %, то повторяют расчет до тех пор,
пока разность между последним значением
числа Rei
и предыдущим Rei–1
не окажется 5 %.
Такой метод решения задачи называется
методом последовательно приближения.
.
По найденной средней скорости определяется
число Re1. Число
Re1 сравнивается
с Reкр,
если разность между Reкр
и вновь рассчитанным Re1
оказывается
5 %, то расчет считают оконченным.
Если же разность оказывается > 5 %, то
по формуле (9.11) определяется величина
1, где уже
вместо Reкр
подставляют значение Re1.
Далее по одной из формул (9.4) или (9.7);
(9.8') или (9.9') определяют значение Q1,
затем – среднею скорость 1
и далее число Re2.
Затем Re2 сравнивают
с Re1, если разность
5 %, то расчет считают
оконченным. Если же разность оказывается
> 5 %, то повторяют расчет до тех пор,
пока разность между последним значением
числа Rei
и предыдущим Rei–1
не окажется 5 %.
Такой метод решения задачи называется
методом последовательно приближения.
В случае турбулентного режима в качестве первого приближения предполагают, что трубопровод работает в области квадратичного сопротивления. Такое предположение позволяет по известным d и определить величину по формуле Шифринсона:
 .
.
По
формулам (9.4) или (9.7) определятся Q.
По найденному Q
рассчитывается Re1.
Далее по формуле
 определяют нижнюю границу области
квадратичного сопротивления. Если Re1
Reкв,
то сделанное предположение подтверждается
и на этом расчет окончен. Если же Re1
Reкв,
то по значению Re1 определяют
в какой области работает трубопровод
(см. модуль 7, п. 3.5 и рис. 7.11). Для этой
области по соответствующей формуле
определяют 1,
затем находят Q1 и далее Re2.
После чего Re2
сравнивают с Re1,
если разность 5 %,
то расчет считают оконченным. Если же
разность оказывается > 5 %, то повторяют
расчет до тех пор, пока разность между
последним значением числа Rei
и предыдущим Rei–1
не окажется
5 %. При этом следят в какой области
сопротивления работает трубопровод и
i
определяют по соответствующей формуле.
определяют нижнюю границу области
квадратичного сопротивления. Если Re1
Reкв,
то сделанное предположение подтверждается
и на этом расчет окончен. Если же Re1
Reкв,
то по значению Re1 определяют
в какой области работает трубопровод
(см. модуль 7, п. 3.5 и рис. 7.11). Для этой
области по соответствующей формуле
определяют 1,
затем находят Q1 и далее Re2.
После чего Re2
сравнивают с Re1,
если разность 5 %,
то расчет считают оконченным. Если же
разность оказывается > 5 %, то повторяют
расчет до тех пор, пока разность между
последним значением числа Rei
и предыдущим Rei–1
не окажется
5 %. При этом следят в какой области
сопротивления работает трубопровод и
i
определяют по соответствующей формуле.
Целесообразно графическое решение задачи, основанное на построении характеристики трубопровода Н = f (Q). Характеристика строится по уравнениям (9.8) или (9.9) с учетом вида истечения жидкости из трубопровода. Для построения графика задаются значениями Q и для каждого Q определяют значение Н. Строят график (рис. 9.5).

По оси ординат откладывается заданный напор Н (известный из задания) и по графику определяется соответствующий ему расход Q.
