8)Свободные затухающие механические колебания, уравнение и характеристики.

Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой.

Затухание свободных механических колебаний вызывается главным образом трением, сопротивлением окружающей среды.

Закон затухания колебаний зависит от свойств колебательной системы.

Колебательная система называется линейной, если параметры, характеризующие физические свойства системы, не изменяются в ходе процесса.

Декремент затухания - отношение двух последних амплитуд, отличающихся условным периодом.

Логарифмический декремент затухания – отношение логарифмов этих амплитуд.

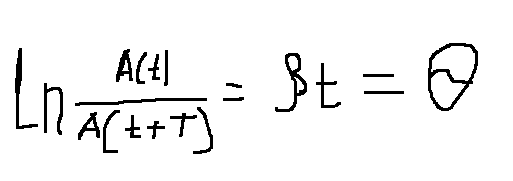
Добротностью колебательной системы называется безразмерная величина Q, равная произведению 2П на отношение энергии колебаний системы в произвольный период времени к убыли этой энергии за условный период.

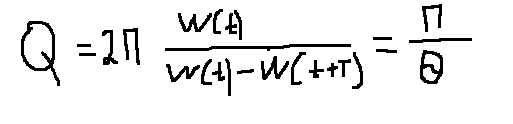
График свободных затухающих колебаний:

9)Вынужденные механические колебания. Резонанс.

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Переменная внешняя сила, приложенная к системе и вызывающая её вынужденные механические колебания, называется вынуждающей или возмущающей силой.

После приложения возмущающей силы к маятнику, у него вначале возникает переходный режим вынужденных колебаний, при котором маятник одновременно участвует в двух колебаниях:

S(t) = x1(t)+x2(t).

Первый член соответствует свободным затухающим колебаниям маятника, а второй соответствует незатухающим периодическим колебаниям маятника.

Амплитудное значение х1(t) = А0 * (е^-βt) более или менее быстро уменьшается после начала вынужденных колебаний: за время t = 4,6/β амплитуда х1(t) уменьшается в 100 раз. Следовательно, через некоторое время t после начала колебаний свободные затухающие колебания маятника практически прекращаются : x1(t) = x2(t). Маятник переходит в состояние установившихся вынужденных колебаний, совершающихся с частотой возмущающей силы.

График вынужденных колебаний:

Резкое возрастание амплитуды вынужденных механических колебаний при приближении циклической частоты ω возмущающей силы к значению Ω называется явлением механического резонанса. Ω =

Графики зависимости А от Ω называются резонансными кривыми.

По мере увеличения коэффициента затухания β пики на резонансных кривых быстро сглаживаются, а резонансная частота Ω медленно уменьшается.

10)Сложение колебаний. Фигуры Лиссажу.

Под сложением колебаний понимают нахождение закона результирующего колебаний системы в тех случаях, когда эта система одновременно участвует в нескольких колебательных процессах. Различают два предельных случая: сложение колебаний одинакового направления и сложение взаимно перпендикулярных колебаний. Первый случай соответствует, например, колебаниям грузика 1, который колеблется относительно грузика 2 на пружине а и вместе с ним на пружине б.

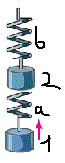
Сложение двух одинаково направленных гармонических колебаний

S1= A1sin(ω1*t+φ1), s2 = A2sin(ω2*t+φ2) можно произвести, воспользовавшись методом векторных диаграмм.

Фазы этих колебаний: Ф1(t) = (ω1*t+φ1) и Ф2 = (ω2*t+φ2),

Результирующему колебанию сооветствует вектор s = A(t)sinФ(t).

По теореме косинусов:

Разность фаз двух гармонических колебаний s1 и s2 равна: Ф2(t)-Ф1(t) = (ω2- ω1)t+( φ2- φ1).

Два колебательных процесса называются когерентными, если их разность фаз со временем остается постоянной.

В зависимости от разности начальных фаз складываемых колебаний амплитуда А результирующих колебаний изменяется в пределах:

от

Аmin=А1-А2 при φ2- φ1 = (2m+1)П.

До

Amax=А1+А2 при φ2- φ1 = 2mП.

, где m – 0,1,2.. – целое число.

Если φ2- φ1 = 2mП, то колебания синфазны(находятся в одной фазе), а если φ2- φ1 = (2m+1)П, то в противофазе.

Негармонические колебания, получающиеся в результате наложения двух одинаково направленных гармонических колебаний с близкими частотами (ω2-ω1<<ω1),называются биениями.

График таких колебаний выглядит так:

Величина A(t), характеризующая размах колебаний при биениях, изменяется в пределах от Amin до Аmax c циклической частотой Ω = ω2-ω1, называемой циклической частотой биений.

Период биений: Т = 2П/Ω.

Сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты.

Пусть точка М одновременно колеблется вдоль осей координат ОХ и ОY по законам: x = A1sin(ωt+φ1), y = A2sin(ωt+φ2).

Уравнение траектории результирующего колебания точки М в плоскости XOY можно найти, исключив из выражений для x и y параметр t

x/A1 = sin(ωt+φ1) = sin(ωt)*cosφ1+cos(ωt)*sinφ1,

y/A2 = sin(ωt+φ2) = sin(ωt)*cosφ2+cos(ωt)*sinφ2.

После преобразования получится уравнение траектории, имеющей вид эллипса:

Ориентация в плоскости XOY эллипса, а также его размеры зависят от амплитуд A1 и A2 складываемых колебаний и разности их начальных фаз.

Если складывать взаимно перпендикулярные колебания с циклическими частотами pω и qω, где p и q – целые числа, то значения координат x и y колеблющейся точки М одновременно повторяются через одинаковые промежутки времени Т, равные общему наименьшему кратному Т1=2П/(pω) и T2 = 2П/(qω). – периодов колебаний вдоль оси OX и OY. Поэтому траектория точки М – замкнутая кривая, форма которой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Такие замкнутые траектории точки М, одновременно совершающей гармонические колебания в двух взаимно перпендикулярных направлениях, называются фигурами Лиссажу.