Рассмотрим теперь неоднородную систему линейных дифференциальных уравнений:

dy^->/dx=A(x)y^->+f^->(x) (6). Теорема. О структуре общего решения линейной неоднородной системы.

Пусть ₁^->(х),......., _n^->(х) – фундаментальная система решений однородной системы (1), а ^->(x) –

частное решение неоднородной системы (6). Тогда общее решение неоднородной системы

записывается в виде: y^->= c_i_i^->(х)+ ^->(x) (7). Доказательство: сначала проверим: является

ли вектор-функция (7) решением неоднородной системы (6)? Для этого подставим (7) в левую часть (6)

d/dx( c_i_i^->(х)+ ^->(x))= c_i(d/dx)_i^->(х)+ (d/dx)^->(x). Поскольку вектор-функции

_i^->(х) (i= ) удовлетворяет однородному уравнению (1), а вектор-функция ^->(x) неоднородному,

то справедливы тождества: (d/dx) _i^->(х)A(x) _i^->(х), (d/dx) ^->(x)A(x) ^->(x)+f^->(x), и поэтому

(d/dx)( c_i_i^->(х)+ ^->(x)) c_iA(x) _i^->(х)+A(x) ^->(x)+ f^->(x)A(x)( c_i _i^->(х)+ ^->(x))+ f^->(x).

Полученное тождество доказывает, что (7) является решением неоднородной системы.

Перейдем к доказательству общности решения. Покажем, что из (7) можно получить любое частное

решение неоднородной системы. Зададим произвольное начальное условие: y^->(x₀)=b^->. Разложим

постоянный вектор b^->-^->(x₀) по системе линейно независимых векторов (базису) ₁^->(х₀),......., _n^->(х₀):

b^->-^->(x₀)= c₁^*₁^->(х₀)+.......+ c_n^*_n^->(х₀). Если теперь в (7) заменить c_i на c_i^*, то полученное частное

решение будет выбранному начальному условию.

Билет №55

Метод вариации произвольных постоянных для отыскания частного решения линейной неоднородной системы.

Существует прием отыскания частного решения линейной неоднородной системы с произвольной

правой частью f^->(x) по известной фундаментальной системе решений ) ₁^->(х),......., _n^->(х) однородной

системы. Будем искать частное решение системы (6) в виде: y^->= c_i(x)_i^->(х) (8), где

c_i(x) (i= )- неизвестные функции. Потребуем, чтобы при подстановке (8) в (6) получалось

тождество. Тогда,

c_i^/(x)_i^->(х)+ c_i(x)_i^->/(х)=A(x) c_i_i^->(х)+f^->(x)

или c_i^/(x)_i^->(х)+ c_i(x)_i^->/(х)-A(x) _i^->(х)=f^->(x). Учитывая, что _i^->(х) – решения однородной

системы, придем к: c_i^/(x)_i^->(х)= f^->(x) (9). В результате пришли к линейной алгебраической

сумме уравнений для неизвестных c_i^/(x),........, c_n^/(x). Определитель неоднородной системы (9) является

определителем Вронского ∆=₁^->(х) ....... _n^->(х) =W(x). Для системы линейно независимых функций

₁^->(х),......., _n^->(х) определитель W(x)0 при всех х. Следовательно, неоднородная линейная

алгебраическая система (9) имеет единственное решение, которое можно записать как

c_i^/(x)=₁(x),.........., c_n^/(x)=_n(x). Вычисляя n неопределенных интегралов без произвольных постоянных

и подставляя их в (8), получаем искомое частное решение.

Билет №56

Линейные однородные системы с постоянными коэффициентами. Характеристическая матрица и характеристическое уравнение. Вид фундаментальной системы решений в случае простых корней (действительных и комплексных).

Рассмотрим подробнее линейную однородную систему уравнений с постоянными коэффициентами:

dy^->/dx=Ay^-> (10), где А – (nxn) матрица постоянных коэффициентов: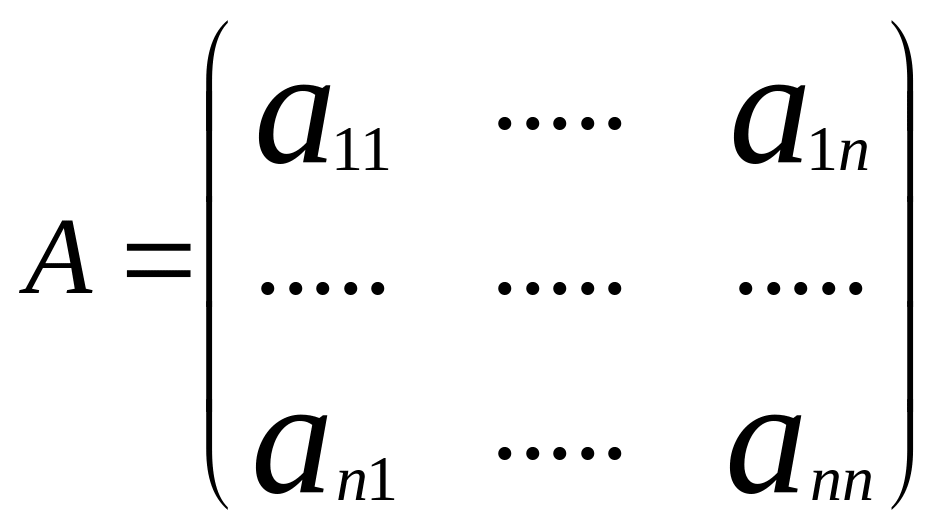

Система (10) удовлетворяет теореме существования во всем пространстве E_n+1. Приемом, который был

рассмотрен ранее, данную систему можно свести к линейному однородному уравнению n-го порядка

для одной из переменных y_k, решение которого, как известно, ищется в виде y_k=_ke^x. Исходя из этих

соображений, будем искать нетривиальное решение однородной системы (10) в форме следующей

вектор – функции: y_k^->=^->e^x (11), где ^-> - неизвестный постоянный вектор,  - неизвестная константа.

Подставляя (11) в (10), придем к: ^->e^x=A^-> e^x или (A-E) ^->=0 (12), где Е=_ij- единичная

матрица. Однородная система (12) имеет ненулевое решение, когда: det(A-E)=0 или

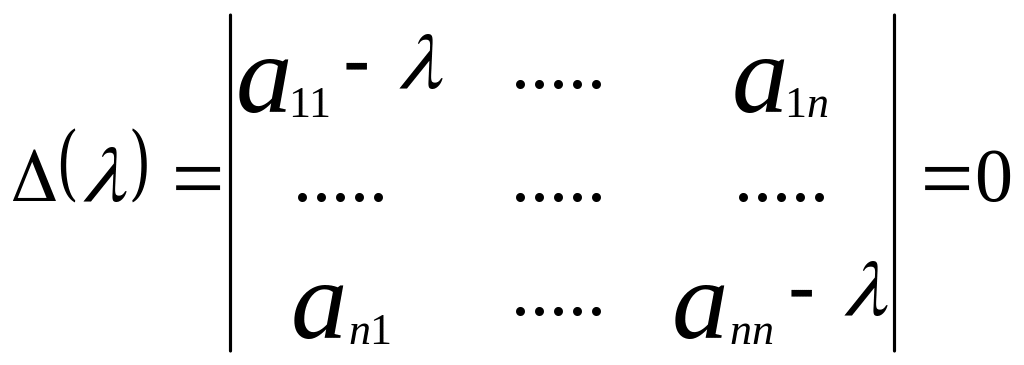(13)

Соотношение (13) представляет собой характеристическое уравнение для определения  (в полной

аналогии с уравнением n-го порядка). Если раскрыть определитель, то левая часть (13) окажется

многочленом n-ой степени по , который называют характеристическим. Вернемся к соотношению

(12), которое можно переписать в виде: А^->=^-> (14). Уравнение (14) – известное из курса

“Аналитическая геометрия и высшая алгебра” уравнение на определение собственных значений  и

собственных векторов ^-> матрицы А. Заметим, что в зависимости от собственных значений матрицы А

вид решений системы (10) может быть весьма различным.

1. Случай простых корней характеристического уравнения.

Пусть все корни характеристического уравнения (13) простые: ₁,........, _n. В этом случае характеристический многочлен ∆() допускает представление в виде: ∆()=(-_k) ∆₁() (15), причем ∆₁(_k)0. Из (15) следует, что: ∆^/()=∆₁()+(-_k) ∆₁^/(), и поэтому ∆₁(_k) =∆₁^/(_k)0. С другой стороны, по правилам дифференцирования функционального определителя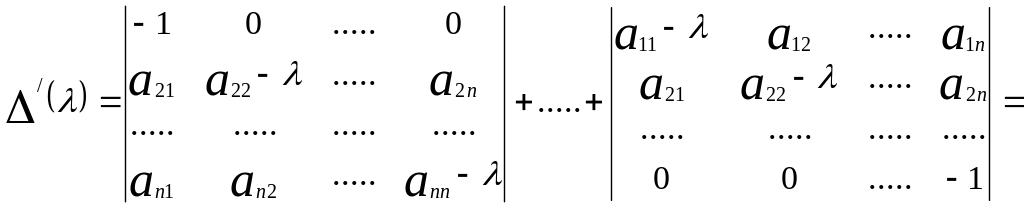

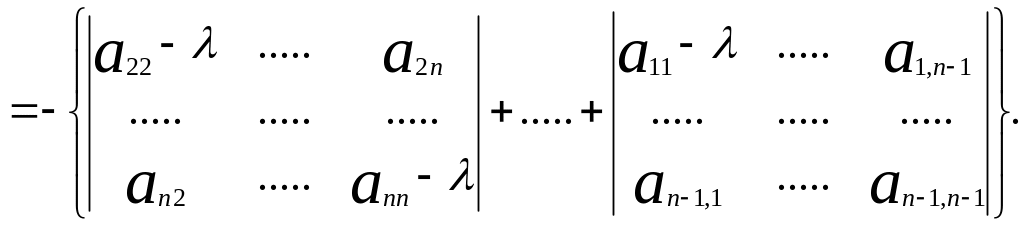
Поскольку сумма диагональных миноров (n-1) порядка матрицы 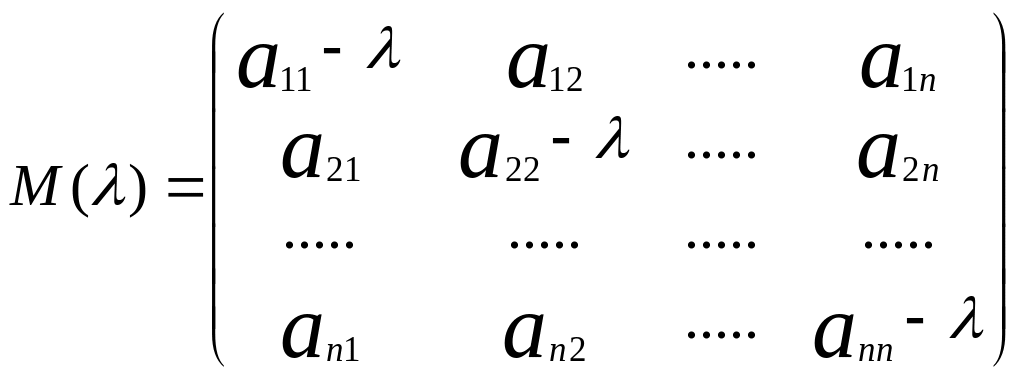при =_k не обращается в нуль, то найдется по крайней мере один из диагональных миноров, отличный от нуля. Это означает, что матрица М(_k) имеет rang М(_k)=r=n-1. Для определения векторов ^-> будем последовательно подставлять в уравнения (12) =₁,........., =_n. В результате придем к уравнению вида: (A-_kE) ^->_k=0 или

M(_k) ^->_k=0 (16). Всего таких систем уравнений будет n, поскольку индекс k пробегает значения от 1 до n. Поскольку, как мы установили, ранг матрицы М(_k): r=n-1, то компоненты собственных векторов ^->_k определяются с точностью до произвольного множителя. В качестве ненулевого решения системы уравнений (16) можно взять алгебраические дополнения элементов той строки матрицы М(_k), которые не обращаются в нуль. Такие миноры существуют, ибо r=n-1. В результате найдем n решений однородной системы (10): ^->_k(x)= ^->_ke^kx_, k=1,2.........,n (17). Теперь необходимо доказать их линейную зависимость. Доказательство проведем методом «от противного». Пусть найденная система решений линейно зависима, т.е. найдутся ненулевые действительные постоянные ₁,........, _n (₁²+......+_n²0) такие, что: ₁^->₁e^1x+..........+_n^->_ne^nx=0 при всех х. Однако ранее было доказано, что функция e^1x,......., e^nx линейно независимы при _i=_j. Поэтому данное равенство имеет место лишь при

₁^->₁=0,.........., _n^->_n=0. Так как не все _k равны нулю, то найдется вектор ^->_i=0, но это не соответствует определению собственных векторов матрицы. Пришли к противоречию. Следовательно, полученная система решений (17) фундаментальна, и общее решение однородной системы (10) представляется в виде: y^->=c₁^->₁e^1x+..........+c_n^->_ne^nx