
- •Билет №1
- •Билет №2
- •Билет №5 Линейные дифференциальные уравнения первого порядка. Структура общего решения линейного неоднородного уравнения. Построение общего решения по известным частным решениям.
- •Билет №9
- •Билет №16
- •Рассмотрим теперь неоднородную систему линейных дифференциальных уравнений:
- •Билет №10
Билет №16
Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Уравнения, не содержащие явно независимой переменной, неизвестной функции.
Уравнением первого порядка, не разрешенным относительно производной, называют дифференциальное уравнение вида
![]() .
(6)
.
(6)
Рассмотрим сначала простые частные случаи уравнения (6).
Пусть функция не зависит от и
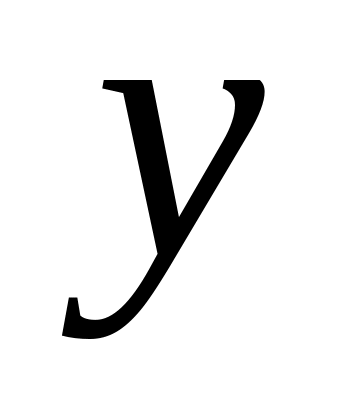 :
:
![]() (7). Предположим,
что это уравнение имеет действительные
корни
(7). Предположим,
что это уравнение имеет действительные
корни
![]() ,
,
![]() ,
… Тогда,
,
… Тогда,
![]() ;
;
![]() 1,2,…
Отсюда,
1,2,…
Отсюда,
![]() - прямые. Поскольку,
- прямые. Поскольку,
![]() ,
то
,
то
![]() .
Это общий интеграл уравнения (7).
.
Это общий интеграл уравнения (7).
Пусть функция не зависит от :
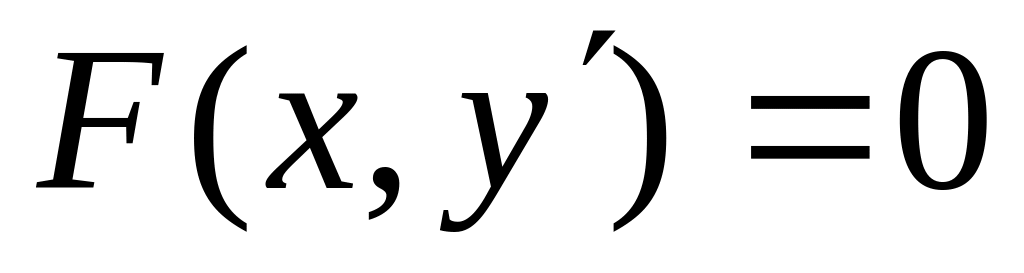 (8). Не всегда это уравнение легко
решается относительно
(8). Не всегда это уравнение легко
решается относительно
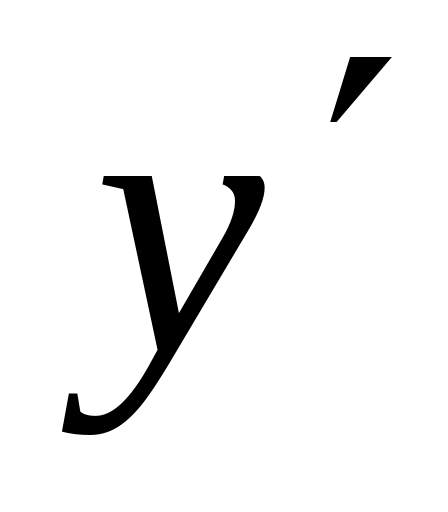 .
Если его удается разрешить, то
.
Если его удается разрешить, то
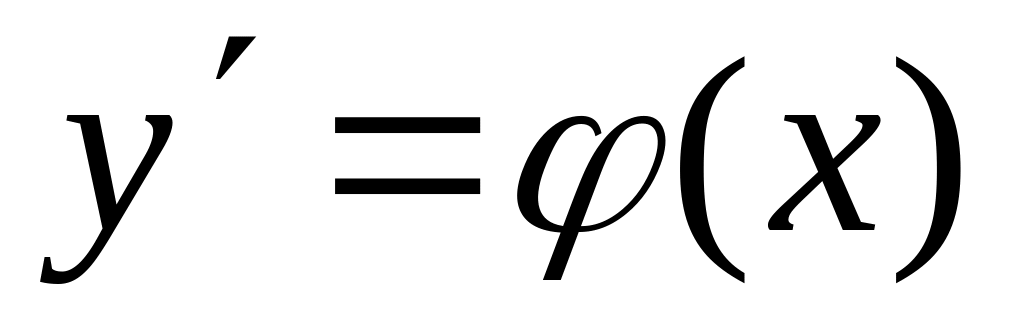 и
и
![]() .
Иногда удается подобрать две функции
.
Иногда удается подобрать две функции
![]() ,
,
![]() такие, что
такие, что
![]() .
Тогда уравнение (8) можно проинтегрировать
в параметрической форме. В самом деле.
.
Тогда уравнение (8) можно проинтегрировать
в параметрической форме. В самом деле.
![]() .
Откуда
.
Откуда
![]() (9). Уравнения (9) представляют собой
общий интеграл уравнения (8) в параметрической
форме. Действительно, если исключить
параметр
(9). Уравнения (9) представляют собой
общий интеграл уравнения (8) в параметрической
форме. Действительно, если исключить
параметр
![]() ,
то получим общий интеграл. Возникает
вопрос: как находить на практике функции
,
то получим общий интеграл. Возникает
вопрос: как находить на практике функции
![]() и
и
![]() ?
Иногда можно дать некоторые рекомендации.
Пусть, например, имеем уравнение вида:
?
Иногда можно дать некоторые рекомендации.
Пусть, например, имеем уравнение вида:
![]() ,
где
,
где
![]() и
и
![]() - однородные многочлены относительно
и
(степени однородности общем случае
разные).
- однородные многочлены относительно
и
(степени однородности общем случае
разные).
Пример.
![]() .
Применим параметризацию
.
Применим параметризацию
![]() .
Заметим, что такую же параметризацию
применяют в уравнении декартова листа:
.
Заметим, что такую же параметризацию
применяют в уравнении декартова листа:
![]() .
Тогда,
.
Тогда,
![]() ,
,
![]() .
.
Отсюда,![]() .
Производя замену переменной
.
Производя замену переменной
![]() ,
вычисляем интеграл
,
вычисляем интеграл
![]()
![]() .
.
Окончательно,
![]() ,
,
![]() .
.
Предположим теперь,
что уравнение (8) разрешается относительно
:
![]() ,
,
т.е.
![]() .
В это случае параметр ввести легко:
.
В это случае параметр ввести легко:
![]() - произвольная дифференцируемая функция.
Тогда,
- произвольная дифференцируемая функция.
Тогда,
![]() ,
и далее проводиться интегрирование
уравнения (8) в параметрической форме.
,
и далее проводиться интегрирование
уравнения (8) в параметрической форме.
3. Пусть, наконец, функция F не зависит от аргумента x: F(y,y')=0 (1). Если уравнение (1) разрешается относительно y’, то далее все ясно – приходим к уравнеию с разделяющимися переменными. Надо поискать (t) и (t) такие, чтобы y=(t), y’=(t) и F((t), (t))0. Тогда, dx=dy/y’=(’(t)dt)/(t) и x=(’(t)dt)/(t) + c; y=(t) – система из двух уравнений, - общий интеграл уравнения (1). Как найти (t) и (t)? Если уравнение (1) легко решается относительно y: y=g(y’) и F(g(y’),y’)0. Тогда можно взять y’=h(t), h(t) – произвольная дифференцируемая функция. В результате, y=g(h(t)) и далее по схеме.
4. Рассмотрим теперь уравнение общего вида: F(x,y,y’)=0 (2), гдк функция F становиться однородной относительно всех своих аргументов, если считать аргумент x измерения 1, аргумент y – измерения , аргумент y’ – измерения (-1), т.е. F(x, y, -1y’)mF(x,y,y’) (3), для любых x, y, y', . Тогда, делая замену функции и аргумента: x=et, y=zet, t – новая независимая переменная, z – новая функция, находим: y’=dy/dx=(dy/dt)(dt/dx); dx/dt=et dt/dx= e-t. Отсюда: y’=(dz/dt + z) ete-t. Подставляя все в (2), (3), придем к: F(et, zet, (dz/dt + z) e(-1) t) em t F(1, z, dz/dt + z)=0. В этом уравнении отсутствует независимая переменная t, и она принимает вид (1): G(z, dz/dt)=0, которое решается указанным выше способом.
Билет №17
Уравнение с однородной функцией. Общий случай введения параметра.
1. Рассмотрим теперь уравнение общего вида: F(x,y,y’)=0 (2), гдк функция F становиться однородной относительно всех своих аргументов, если считать аргумент x измерения 1, аргумент y – измерения , аргумент y’ – измерения (-1), т.е. F(x, y, -1y’)mF(x,y,y’) (3), для любых x, y, y', . Тогда, делая замену функции и аргумента: x=et, y=ze t, t – новая независимая переменная, z – новая функция, находим: y’=dy/dx=(dy/dt)(dt/dx); dx/dt=et dt/dx= e-t. Отсюда: y’=(dz/dt + z) e te-t. Подставляя все в (2), (3), придем к: F(et, ze t, (dz/dt + z) e( -1) t) em t F(1, z, dz/dt + z)=0. В этом уравнении отсутствует независимая переменная t, и она принимает вид (1): G(z, dz/dt)=0, которое решается указанным выше способом.
2. Рассмотрим снова уравнение: F(x,y,y’)=0 (2) с функцией F общего вида. Предположим, что каким-то образом удалось представить: x=(u,); y=(u,); y’=(u,) – система из трех уравнений, так что выполняется тождество по (u,): F((u,), (u,), (u,))0. Покажем, что в этом случае удалось перейти к уравнению, разрешенному относительно производной. В самом деле: dy=y’dx (/u)du + (/)d=(u,)[(/u)du + (/)d]. Пусть u – новая независимая переменная, а - новая функция. Тогда: d/du = (/u-(/u))/((/)-/) (4). Допустим, что мы нашли общее решение уравнения (4): =(u,c). Тогда решение исходного уравнения (2) получается в виде: x=(u,(u,c)); y=(u,(u,c)) – система из двух уравнений. Это общий интеграл уравнения (2) в параметрической форме.
Билет №18
Дифференциальные уравнения, разрешимые относительно аргумента или функции. Уравнение Лагранжа.
Рассмотрим еще два частных случая, когда параметрическое представление получается просто. Пусть, например, уравнение: F(x,y,y’)=0 (2) допускает представление в виде: y=f(x,y’) (5). Тогда в качестве вышеупомянутых параметров можно выбрать x и y’=p, т.е.: x=x; y=f(x,p); y’=p –система из трех уравнений. В результате из равенства: dy=y’dx имеем: (f/x)dx + (f/p)dp=pdx или: dp/dx=(p -f/x)/(f/p). Решая уравнение, получим: p=(x,c). Таким образом, общее решение исходного уравнения (5) имеет вид: y=f(x,(x,c)). В том случае, когда уравнение (2) допускает запись в виде: x=g(y,y’) (6), параметрами считаем y и y’=p, т.е.: x=g(y,p); y=y; y’=p – система из трех уравнений. Тогда: dx=dy/y’ (g/y)dy + (g/p)dp=dy/p. Отсюда: dp/dy=(1/p - g/y)/(g/p). Если мы получим решение уравнения в виде p=(y,c), то общее решение уравнения (6) таково: x=g(y,(y,c)).
Проанализируем уравнение вида: y=x(y’) + (y’) (7), где и - дифференцируемые функции. Данное уравнение, в которое переменные x и y входят линейно, носит название уравнение Лагранжа. Найдем общее решение данного уравнения. Обозначим y’=p. Тогда, y=x(p) + (p), и поэтому: dy=pdx=(p)dx + x’(p)dp + ’(p)dp (8). Получилось линейное дифференциальное уравнение, если считать x – функцией, а p – независимой переменной: [p-(p)]dx/dp - x’(p)=’(p). Может оказаться, что p(p). Этот случай соответствует специальному уравнению Лагранжа, мы его исследуем позже. Предположим, что уравнение p-(p)=0 имеет решения p1, p2…. Тогда при подстановке p= pi в уравнение (8) оно превращается в тождество. Значиться: y=x(pi) + (pi) (9) – интегральные прямые уравнения Лагранжа. При p<> pi, имеем: dx/dp + ’(p)x / ((p) - p) = ’(p)/(p-(p)) (10). Если применить методы решения линейных дифференциальных уравнений, то общее решение уравнения (10) можно записать в виде: x=c(p) + (p). Вместе с выражением y=x(p) + (p) оно дает параметрическое представление искомого общего решения.
Билет №19
Уравнение Клеро. Понятия С-дискриминантной кривой и огибающей семейства кривых, их связь. Теорема об огибающей семейства интегральных кривых.
Проанализируем подробнее ситуацию, когда p(p). В этом случае уравнение: y=x(y’) + (y’) (7) превращается в: y=xy’ + (y’) (11), и носит название уравнения Клеро. Полагая (p)=р в уравнении: dy=pdx=(p)dx + x’(p)dp + ’(p)dp (8), придем к: [x+(p)]dp=0. Далее возможны два случая: а) dp=0 p=c, и тогда: y=xc + (c) (12) – общее решение уравнения Клеро; б) x+’(p)=0. Это уравнение определяет р как функцию x: p=(x). Тогда из (11) имеем: y=x(x) + ((x)) (13). Это будет также решение уравнения Клеро, причем особое. В каждой его точке нарушается единственность. В самом деле. Продифференцируем (12) по с. Тогда получим: 0 = x + ’(c). В дифференциальной геометрии доказывается, что если имеется уравнение (x,y,c)=0, то вместе с уравнением c'(x,y,c)=0 оно представляет С- дискриминантную кривую, и если к тому же: (/x)2 + (/y)2 <>0 и /x, /y ограничены, то С – дискриминантная кривая определяет огибающую семейства кривых.
Определение. Огибающей семейства кривых называется кривая, которая в каждой точке касается одной из кривых семейства. Оказывается всегда для уравнения Клеро С – дискриминантная кривая является огибающей. В самом деле: (x,y,c)=xc+(c)-y. Тогда, /x=c; /y= -1 c2 +1<>0. К тому же /x, /y ограничены.
Поговорим
об особых решениях уравнения F(x,y,y’)=0.
Как следует из теоремы об особых решениях,
особые решения могут быть, если:1)
F/y
- не ограничена; 2)
F/y’=
0.Первый
случай на практике встречается редко.
Поэтому остановимся подробнее на второй
ситуации. Уравнения
![]() определяют
на плоскости кривую (у\-параметр), которая
носит название р-дискриминантной
кривой.
Особое решение уравнения может входить
в состав данной кривой.
определяют
на плоскости кривую (у\-параметр), которая
носит название р-дискриминантной
кривой.
Особое решение уравнения может входить
в состав данной кривой.
Теорема. Огибающая семейства интегральных кривых всегда является особым решением дифференциального уравнения. Доказательство: каждая точка огибающей является одновременно и точкой интегральной кривой, поскольку в каждой своей точке она касается одной из интегральных кривых. Это означает, что в каждой своей точке огибающая имеет направление поля. Значит, она также является интегральной линией дифференциального уравнения, т.е. его решением. Но поскольку через каждую точку проходят два решения (в заданном направлении) - она сама и другая интегральная кривая, то огибающая является особым решением.
Билет №20
Теорема существования решения уравнения первого порядка, неразрешенного относительно производной. P-дискриминантная кривая и особые решения.
Поговорим об особых решениях уравнения F(x,y,y’)=0. Как следует из теоремы об особых решениях, особые решения могут быть, если:1) F/y - не ограничена; 2) F/y’= 0.Первый случай на практике встречается редко. Поэтому остановимся подробнее на второй ситуации. Уравнения определяют на плоскости кривую (у\-параметр), которая носит название р-дискриминантной кривой. Особое решение уравнения может входить в состав данной кривой. Теорема. Огибающая семейства интегральных кривых всегда является особым решением дифференциального уравнения. Доказательство: каждая точка огибающей является одновременно и точкой интегральной кривой, поскольку в каждой своей точке она касается одной из интегральных кривых. Это означает, что в каждой своей точке огибающая имеет направление поля. Значит, она также является интегральной линией дифференциального уравнения, т.е. его решением. Но поскольку через каждую точку проходят два решения (в заданном направлении) - она сама и другая интегральная кривая, то огибающая является особым решением.
Биле №21
Сведение уравнения n-го порядка, разрешенного относительно производной, к нормальной системе уравнений. Теорема существования и единственности решения уравнения n-го порядка, разрешенного относительно старшей производной, как следствие теоремы существования и единственности решения нормальной системы.
1.
Дифференциальное уравнение n-го
порядка, разрешенное относительно
старшей производной. Как
мы уже отмечали, дифференциальным
уравнением n-го
порядка называется соотношение вида:
F(x,y,y',y'',…,y(n))=0.
(1)
Допустим, что уравнение (1) разрешено
относительно старшей производной:
y(n)=f(x,y,y’,y’’,…,y(n-1))
(2).
Далее удобно уравнение (2) свести к
системе диф. уравнений первого порядка.
Сделаем замены, вводя новые функции
у1,у2,…,уn:
у=у1,
у’=y2,
y’’=y3,…,y(n-1)=yn
(3).
Тогда диф. Уравнение (2) будет эквивалентно
следующей системе: dy1/dx=y2,
dy2/dx=y3,…,dyn-1/dx=yn,
dyn/dx=f(x,y1,y2,…,yn)
(4).
Подобная системе диф. Уравнений называется
нормальной.
Общий вид нормальной системы диф.
Уравнений таков: dy1/dx=f1(x,y1,y2,…,yn),
dy2/dx=f2(x,y1,y2,…,yn),…,
dyn/dx=fn(x,y1,y2,…,yn)
(5).Вводя
векторные обозначения
![]() ,
,
![]() ,
получаем сокращенную форму записи (5)
,
получаем сокращенную форму записи (5)
![]() .Теорема
существования и единственности решения
нормальной системы дифференциальных
уравнений. Пусть: 1.
Правые части системы (5) являются
непрерывными функциями по совокупности
аргументов (х,y1,у2,…,уn)
в некоторой области G
(п+1)-мерного
пространства, содержащей
начальную
точку (х0,у10,у20,…,уn0).
2.
Существуют ограниченные производные:
|fi/yk|N,
I=1,n;
k=1,n.
Тогда система (5) имеет единственное
решение: у1=1(х),
у2=2(х),…,уn=n(x),
удовлетворяющее начальному условию:
1(х0)=у10,
2(х0)=у20,…,n(x0)=yn0
и определенное в некоторой окрестности
начальной точки: |x—x0|h.
Без доказательства. Заметим, что в
векторной форме решение системы (5)
записывается в виде
.Теорема
существования и единственности решения
нормальной системы дифференциальных
уравнений. Пусть: 1.
Правые части системы (5) являются
непрерывными функциями по совокупности
аргументов (х,y1,у2,…,уn)
в некоторой области G
(п+1)-мерного
пространства, содержащей
начальную
точку (х0,у10,у20,…,уn0).
2.
Существуют ограниченные производные:
|fi/yk|N,
I=1,n;
k=1,n.
Тогда система (5) имеет единственное
решение: у1=1(х),
у2=2(х),…,уn=n(x),
удовлетворяющее начальному условию:
1(х0)=у10,
2(х0)=у20,…,n(x0)=yn0
и определенное в некоторой окрестности
начальной точки: |x—x0|h.
Без доказательства. Заметим, что в
векторной форме решение системы (5)
записывается в виде
![]() ,
причем
,
причем
![]() .
Доказательство
теоремы очень похоже на доказательство
теоремы о существовании решения одного
дифференциального уравнения первого
порядка, поэтому здесь не приводится.
Аналогичным образом доказывается
возможность продолжения решения,
непрерывная зависимость от начальных
условий и т.д. Поговорим о геометрической
интерпретации решения системы
дифференциальных уравнений. Общее
решение системы представляет собой
семейство интегральных кривых в
(п+1)-мерном пространстве и зависит от n
параметров (при фиксированном x0
- параметры у10,y20,...,уn0.)
Отсюда следует вывод, что общее решение
системы дифференциальных уравнений
(5) зависит от n
произвольных постоянных. Частное решение
можно интерпретировать как параметрически
заданную (x
- параметр) кривую в n-мерном
пространстве {y1,у2,…,уn},
которую часто называют траекторией
движения
системы (5). На основе сформулированной
общей теоремы докажем теорему для
уравнения (2). Теорема
существования и единственности решения
дифференциального уравнения n-го порядка,
разрешенного относительно старшей
производной. Пусть в уравнении (2) функция
f(x,y,y’,y’’,…,y(n-1))
непрерывна по совокупности переменных
в некоторой области G
(n+1)-мерного
пространства и существуют ограниченные
производные |f/y(k)|N,
k=0,1
во всей области G.
Начальная точка (x0,y0,y0’,…,y0(n-1))G.
Тогда; существует единственное решение
уравнения
(2); удовлетворяющее начальному условию
(x0,y0,y0’,…,y0(n-1)),
т.е.
(х0)=у0,
’(x0)=y’0,
…,(n-1)(x0)=y0(n-1),
определенное в окрестности точки х0:
|x-x0|h.
Доказательство.
Поскольку нормальная система (4);
соответствующая уравнению (2), является
частным случаем системы (5), то можно
проверить условия теоремы для системы
(5). Первые (п — 1) правых частей системы
(4) удовлетворяют условиям теоремы
существовать: fk=yk-1
-
непрерывны
и
.
Доказательство
теоремы очень похоже на доказательство
теоремы о существовании решения одного
дифференциального уравнения первого
порядка, поэтому здесь не приводится.
Аналогичным образом доказывается
возможность продолжения решения,
непрерывная зависимость от начальных
условий и т.д. Поговорим о геометрической
интерпретации решения системы
дифференциальных уравнений. Общее
решение системы представляет собой
семейство интегральных кривых в
(п+1)-мерном пространстве и зависит от n
параметров (при фиксированном x0
- параметры у10,y20,...,уn0.)
Отсюда следует вывод, что общее решение
системы дифференциальных уравнений
(5) зависит от n
произвольных постоянных. Частное решение
можно интерпретировать как параметрически
заданную (x
- параметр) кривую в n-мерном
пространстве {y1,у2,…,уn},
которую часто называют траекторией
движения
системы (5). На основе сформулированной
общей теоремы докажем теорему для
уравнения (2). Теорема
существования и единственности решения
дифференциального уравнения n-го порядка,
разрешенного относительно старшей
производной. Пусть в уравнении (2) функция
f(x,y,y’,y’’,…,y(n-1))
непрерывна по совокупности переменных
в некоторой области G
(n+1)-мерного
пространства и существуют ограниченные
производные |f/y(k)|N,
k=0,1
во всей области G.
Начальная точка (x0,y0,y0’,…,y0(n-1))G.
Тогда; существует единственное решение
уравнения
(2); удовлетворяющее начальному условию
(x0,y0,y0’,…,y0(n-1)),
т.е.
(х0)=у0,
’(x0)=y’0,
…,(n-1)(x0)=y0(n-1),
определенное в окрестности точки х0:
|x-x0|h.
Доказательство.
Поскольку нормальная система (4);
соответствующая уравнению (2), является
частным случаем системы (5), то можно
проверить условия теоремы для системы
(5). Первые (п — 1) правых частей системы
(4) удовлетворяют условиям теоремы
существовать: fk=yk-1
-
непрерывны
и
![]() -символ
Кронекера, т.е. они и ограничены. Остается
рассмотреть правую часть последнего
уравнения системы (4):fn=f.
Непрерывность функции fn
по совокупности переменных вытекает
из условий теоремы и замен (3). Ограниченность
fk/yi
следует из условий ограниченности
f/y(i)
и замен (3). Следовательно, все условия
общей теоремы выполняются и в окрестности
точки х0:
|х-х0|h
существует единственное решение у=(х).
Каковы начальные условия для него ? Для
общей системы это (х0,у10,у20,…,уn0),
а
на нашем языке -(x0,y0,y0’,…,y0(n-1)),
поскольку у1=(х),
у2=’(х),…,уn=(n-1)(x)
согласно (3).
-символ
Кронекера, т.е. они и ограничены. Остается
рассмотреть правую часть последнего
уравнения системы (4):fn=f.
Непрерывность функции fn
по совокупности переменных вытекает
из условий теоремы и замен (3). Ограниченность
fk/yi
следует из условий ограниченности
f/y(i)
и замен (3). Следовательно, все условия
общей теоремы выполняются и в окрестности
точки х0:
|х-х0|h
существует единственное решение у=(х).
Каковы начальные условия для него ? Для
общей системы это (х0,у10,у20,…,уn0),
а
на нашем языке -(x0,y0,y0’,…,y0(n-1)),
поскольку у1=(х),
у2=’(х),…,уn=(n-1)(x)
согласно (3).
---------------------?????????????
Билет №28
Построение линейного однородного дифференциального уравнения n-го порядка по фундаментальной системе решений.
Следствие. Фундаментальная система решений однозначно определяет линейное однородное дифференциальное уравнения.
Указанное следствие позволяет сформулировать следующую задачу.
Задача. Задана фундаментальная система решений некоторого линейного однородного дифференциального уравнения. Построить дифференциальное уравнение, которое имеет эту фундаментальную систему решений.
Решение.
Пусть
![]() -система
линейно независимых n
раз дифференцируемых функций на отрезке
[a,b].
Составить определитель
-система
линейно независимых n
раз дифференцируемых функций на отрезке
[a,b].
Составить определитель


Данное равенство
представляет собой однородное линейное
дифференциальное уравнение n-го
порядка для неизвестной функции y(x).
Подстановка вместо y(x)
любой функции
![]() обращает уравнение в тождество ( возникают
два одинаковых столбца в определителе).
Это означает, что функции
обращает уравнение в тождество ( возникают
два одинаковых столбца в определителе).
Это означает, что функции
![]() являются
линейно независимыми решениями
построенного уравнения, т.е. его
фундаментальной системой решения.
Коэффициентом при старшей производной
являются
линейно независимыми решениями
построенного уравнения, т.е. его
фундаментальной системой решения.
Коэффициентом при старшей производной
![]() , входящей в уравнение, является
определитель Вронского
, входящей в уравнение, является
определитель Вронского
![]() Для фундаментальной системы решений
Для фундаментальной системы решений
![]() ни в одной точке отрезка [a,b]
, и поэтому на него можно поделить обе
части уравнения. Раскладывая определитель
по последнему столбцу и деля обе части
равенства на W(x)
, придем к однородному линейному
дифференциальному уравнению вида :
ни в одной точке отрезка [a,b]
, и поэтому на него можно поделить обе
части уравнения. Раскладывая определитель
по последнему столбцу и деля обе части
равенства на W(x)
, придем к однородному линейному
дифференциальному уравнению вида :
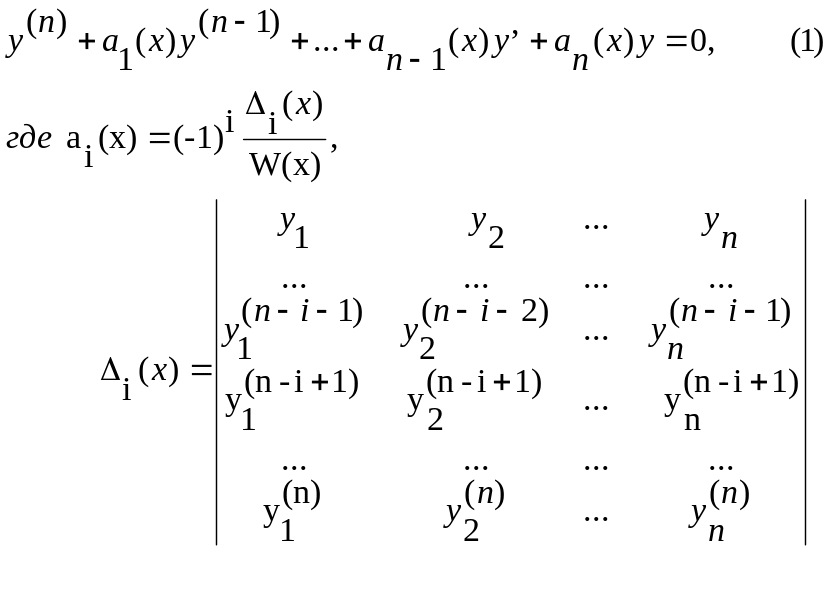
В частности
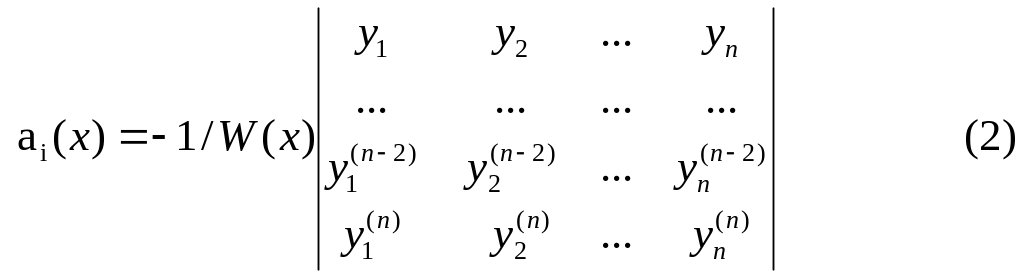
таким образом, искомое уравнение построено.
Билет №29
Правило дифференцирования функционального определителя. Формула Лиувилля. Применение формулы Лиувилля для понижения порядка линейного однородного уравнения 2-го порядка.
Выведем сначала формулу дифференцирования функционального определителя.
Рассмотрим
производную
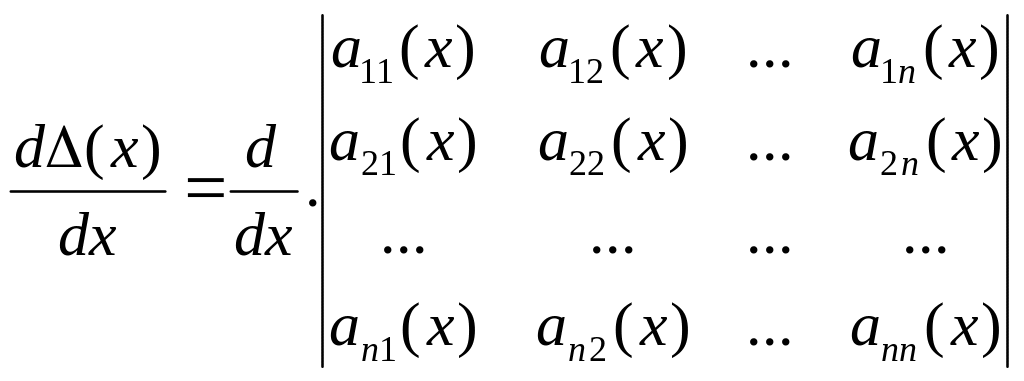
Воспользуемся
формулой для определителя
![]()
Где сумма содержит
n!
Слагаемых, соответствующих различным
упорядоченным множествам
![]() , получаемых r
попарными перестановками (транспозициями)
элементов из множества (1,2,…,n).
Тогда ,
, получаемых r
попарными перестановками (транспозициями)
элементов из множества (1,2,…,n).
Тогда ,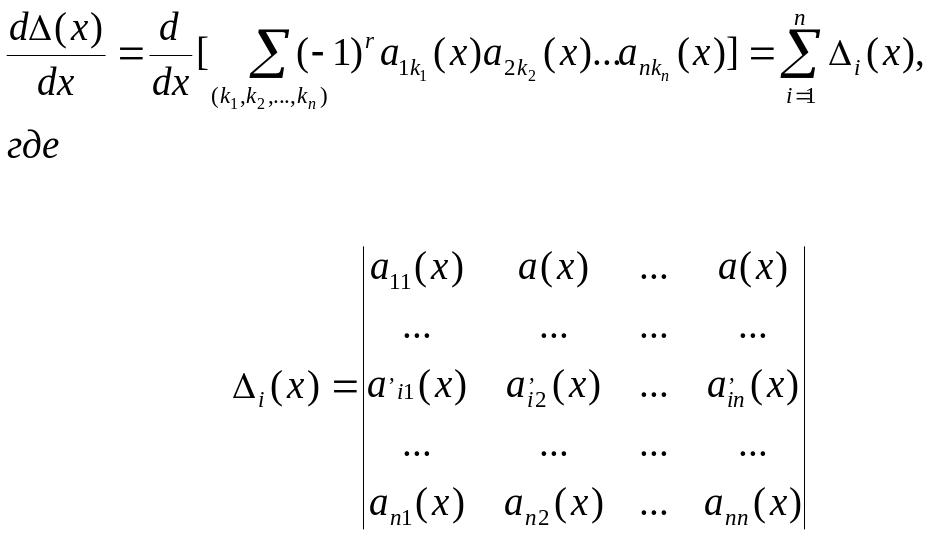
Применяя найденную формулу, подсчитаем производную определителя Вронского W’(x).
 Поскольку
все определители, кроме последнего,
зануляются (содержат одинаковые строки),
то в соответствии с формулой
Поскольку
все определители, кроме последнего,
зануляются (содержат одинаковые строки),
то в соответствии с формулой
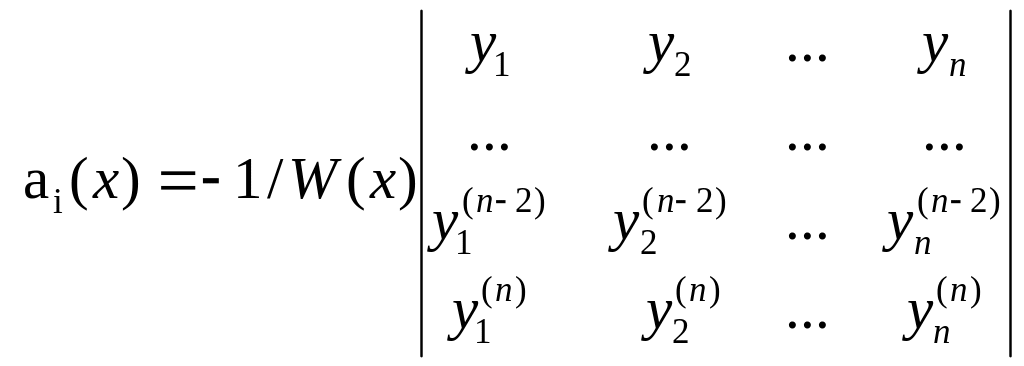 (2)
(2)
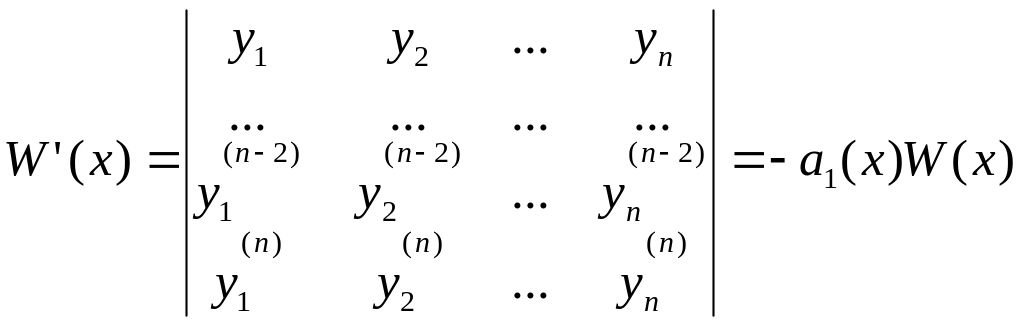
Решая полученное
дифференциальное уравнение первого
порядка, находим :
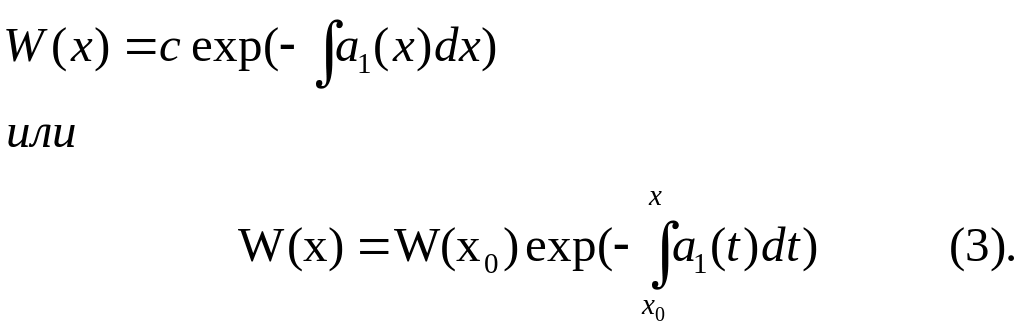
Формула (3) и называется формулой Лиувилля. Из нее отчетливо видно, что если W(x)=0 в одной точке, то он тождественно равен нулю.
На практике
выведенную формулу Лиувилля можно с
успехом применять для отыскания
взаимосвязи фундаментальных решений
линейного однородного дифференциального
уравнения. Рассмотрим линейное однородное
дифференциальное уравнение второго
порядка общего вида
![]() Пусть известно частное решение
Пусть известно частное решение
![]() этого уравнения. Построим систему
фундаментальных решений, взяв в качестве
одного из них
,
а второе определив из формулы Лиувилля.
В самом деле, согласно (3)
этого уравнения. Построим систему
фундаментальных решений, взяв в качестве
одного из них
,
а второе определив из формулы Лиувилля.
В самом деле, согласно (3)
![]()
Откуда,
![]()
Или
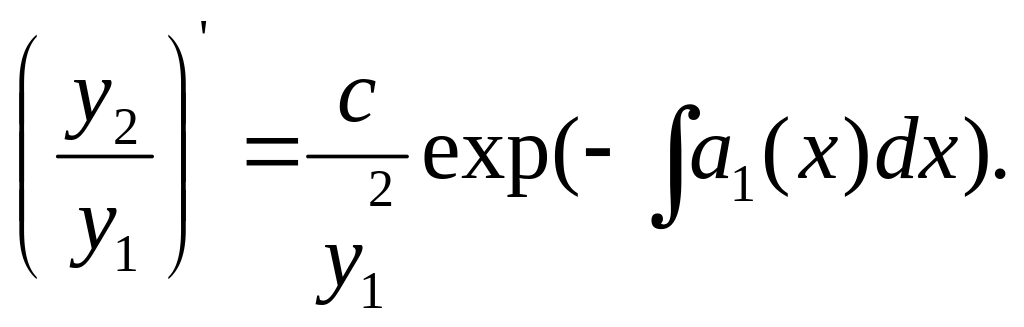
Проводя интегрирование,
получаем формулу связи фундаментальных
решений в виде двух квадратур
![]()
(константа С отнесена в множитель функции ).
Билет №30
Способ понижения порядка линейного однородного дифференциального уравнения, когда известно его частное решение.
Как понизить порядок однородного линейного дифференциального уравнения?
Один прием мы рассматривали ранее = замену функции
![]()
При этом уравнения для новой функции z(x) оказывается уже нелинейным. Оказывается, если известно какое-либо частное решение , то порядок уравнения можно понизить, сохранив его линейность.
Введем новую
функцию z(x)
соотношением
![]() Тогда
,
Тогда
,
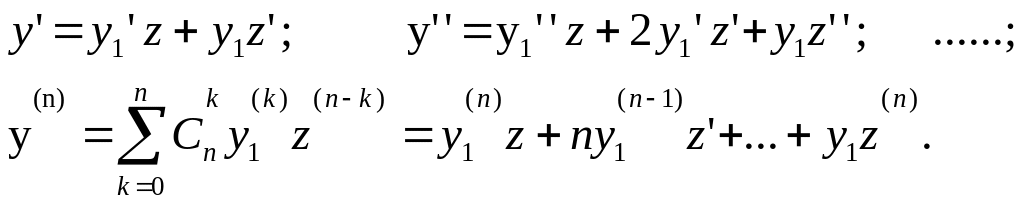
Подставляя все в
однородное дифференциальное уравнение:
![]() ,
придем к
,
придем к
![]()
где оператор
![]() ,
по прежнему ,
,
по прежнему ,
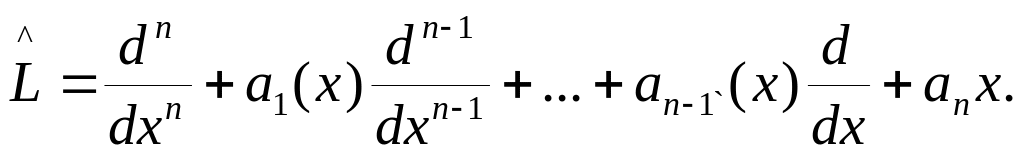
Поскольку
![]() - решение дифференциального уравнения,
- решение дифференциального уравнения,
![]() и в результате получаем линейное
однородное дифференциальное уравнение,
не содержащее явно функции z
. Вводя еще одну функцию u=z’
и деля обе части уравнения на функцию
и в результате получаем линейное
однородное дифференциальное уравнение,
не содержащее явно функции z
. Вводя еще одну функцию u=z’
и деля обе части уравнения на функцию
![]() приходим к
приходим к
![]() где
где
![]() .
.
Полученное уравнение
(n-1)-го
порядка имеет фундаментальную систему
решений
![]() Вспоминая
замены :
Вспоминая
замены :
![]() для
исходного дифференциального уравнения
находим систему решений :
для
исходного дифференциального уравнения
находим систему решений :![]()
Если система
![]() -фундаментальная, то полученная система
решений также фундаментальна.
-фундаментальная, то полученная система
решений также фундаментальна.
Билет №31
Структура общего решения линейного неоднородного дифференциального уравнения n-го порядка. Принцип суперпозиции.
Поговорим теперь о свойствах решений неоднородного уравнения
![]() (5)
(5)
Теорема 1 .О структуре общего решения неоднородного уравнения.
Общее
решение линейного неоднородного
дифференциального уравнения является
суперпозицией частного решения
неоднородного уравнения и общего решения
соответствующего однородного уравнения.
Доказательство
: пусть
Y(x)
– частное решение уравнения (5), т.е.
![]() .
.
Пусть
![]() -
фундаментальная система решений
соответствующего однородного уравнения,
т.е.
-
фундаментальная система решений
соответствующего однородного уравнения,
т.е.
![]() . Докажем, что функция
. Докажем, что функция
![]() (6)
(6)
Являются общим решением дифференциального уравнения (5).
Покажем вначале,
что это просто решение. В самом деле , в
силу линейных свойств оператора
![]()
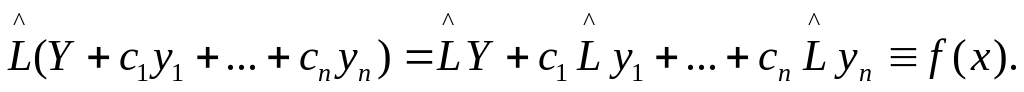
Докажем теперь
общность решения. Зададим произвольные
начальные условия
![]() Подставляя функцию (6) в начальные условия
и вводя обозначения
Подставляя функцию (6) в начальные условия
и вводя обозначения
![]() придем
к системе уравнений
придем
к системе уравнений
![]()
Это – неоднородная
система алгебраических уравнений
относительно неизвестных постоянных
![]() с определителем
с определителем
![]() . Такая система имеет единственное
решение:
. Такая система имеет единственное
решение:
![]() Следовательно
, функция
Следовательно
, функция
![]()
![]() определяет частное решение, удовлетворяющее
заданным начальным условиям.
определяет частное решение, удовлетворяющее
заданным начальным условиям.
Теорема 2. Принцип суперпозиции .
Пусть правая часть
неоднородного уравнения (5):
![]()
И
![]() -
частные решения ду (5):
-
частные решения ду (5):
![]()
Тогда суперпозиция
![]() является
частным решением ду (5)
является
частным решением ду (5)
Доказательство:
Проверим,
что функция
удовлетворяет неоднородному уравнению.
В самом деле

Билет №32
Метод вариации произвольных постоянных для отыскания частного решения линейного неоднородного дифференциального уравнения n-го порядка. Интегральная запись частного решения. Функция Грина.
Покажем, что с
помощью известной фундаментальной
системы решений
![]() линейного однородного уравнения можно
найти частное решение неоднородного
ду
линейного однородного уравнения можно
найти частное решение неоднородного
ду
![]()
и, следовательно
, построить его общее решение. Воспользуемся
тем , что общее решение однородного
уравнения представляется в виде
суперпозиции
![]()
Совершенно ясно,
что ни при каких постоянных
![]() функция (2) не будет решением неоднородного
уравнения (1) . Попытаемся, считая
постоянные функциями
функция (2) не будет решением неоднородного
уравнения (1) . Попытаемся, считая
постоянные функциями
![]() подобрать их так . чтобы функция (2) стала
решением неоднородного уравнения (1).
подобрать их так . чтобы функция (2) стала
решением неоднородного уравнения (1).
Поскольку вместо
одной неизвестной функции y(x)
мы ввели n
функций, то мы имеем право наложить
(n-1)
Условий на
![]() так , как нам удобно. Продифференцируем
обе части выражения (2):
так , как нам удобно. Продифференцируем
обе части выражения (2):
![]()
Потребуем, чтобы
y’
имела такое же выражение как и при
постоянных
![]() т.е.
положим
т.е.
положим
![]()
Дифференцируя еще
раз соотношение для
![]() находим :
находим :
![]() Опять потребуем, чтобы выражение для
y’’
выглядело также как и при постоянных
Опять потребуем, чтобы выражение для
y’’
выглядело также как и при постоянных![]() В
результате получаем еще одно условие
В
результате получаем еще одно условие
![]()
Поступая далее аналогичным образом, можно придти к выражению для (n-1) производной
вида
![]()
наложив (n-1) вспомогательных условий на функцию . Последнее из этих условий таково:
![]()
![]()
продифференцируем соотношение для (n-1) – ой производной еще раз. В результате придем к
![]()
Подстановка выражений для производных в уравнение (1) дает:
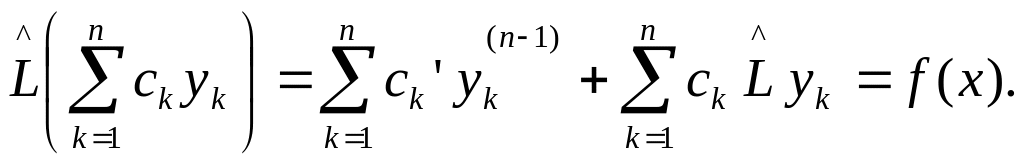
Поскольку
функция![]() -решения
однородного уравнения:
-решения
однородного уравнения:![]() мы
получаем еще одно уравнение для
производных функций
:
мы
получаем еще одно уравнение для
производных функций
:
![]()
Собирая уравненяи
(3-6), получаем неоднородную систему
алгебраических уравнений для производных
неизвестных функций
:
![]()
В силу фундаментальности
системы решений
определитель неоднородной системы (7),
являющейся определителем Вронского,
![]() для любых x.
Поэтому неоднородная система имеет
одно единственное решение:
для любых x.
Поэтому неоднородная система имеет
одно единственное решение:
![]() . Интегрируя эти соотношения (без
произвольных постоянных), находим
. Интегрируя эти соотношения (без
произвольных постоянных), находим
![]() Подставляя
эти выражения в (2) , определяем частное
решение неоднородного уравнения (1).
Рассмотренный метод связан с достаточно
сложными расчетами (решение линейной
системы n
-го порядка и последующее взятие n
квадратур), но позволяет найти частное
решение при любой функции f(x).
Подставляя
эти выражения в (2) , определяем частное
решение неоднородного уравнения (1).
Рассмотренный метод связан с достаточно
сложными расчетами (решение линейной
системы n
-го порядка и последующее взятие n
квадратур), но позволяет найти частное
решение при любой функции f(x).
Билет №33
Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами. Характеристический многочлен и характеристическое уравнение. Построение фундаментальной системы решений линейного однородного уравнения с постоянными коэффициентами в случае простых корней характеристического многочлена (действительных и комплексных)
Перейдем к анализу
линейного однородного дифференциального
уравнения n –го порядка с постоянными
коэффициентами![]() Где
Где
![]() .
Попытаемся найти фундамент. систему
решений уравнения (8).
.
Попытаемся найти фундамент. систему
решений уравнения (8).
Введём оператор дифференцирования D: y’=Dy. Тогда y’’=(y’)’=D(Dy)=D2y, … y(n)=Dny. Уравнение
(8) при этом примет вид Dny+a1Dn-1y+…+ an-1Dy+ any=0 или
(Dn+a1Dn-1+…+ an-1D+an)y=0 Многочлен, стоящий перед функцией y, является многочленом от оператора дифференцирования и носит названия операторного многочлена M(D):
![]()
Операторный
многочлен можно разложить на множители.
Введем характеристический многочлен
![]()
Этот многочлен
имеет n
корней и представим по теореме алгебры
в виде
![]() Значит,
Значит,
![]()
Допустим, что
характеристический многочлен (9) имеет
n
различных корней
![]() .
Тогда из (10) имеем
.
Тогда из (10) имеем
![]()
Поскольку операторы, стоящие в (11) в скобках, обладают переместительным свойством, то любой из них можно сделать последним. Это означает, что уравнение (11) имеет решения:
![]()
Здесь постоянные
![]() могут
быть и комплексными. В итоге, мы получили
n
решений. Можно ли по ним построить общее
решение ? Если найденные решения линейно
независимы, т.е. образуют фундаментальную
систему, то можно. Докажем фундаментальность
найденной системы решений. Составим
определитель Вронского
могут
быть и комплексными. В итоге, мы получили
n
решений. Можно ли по ним построить общее
решение ? Если найденные решения линейно
независимы, т.е. образуют фундаментальную
систему, то можно. Докажем фундаментальность
найденной системы решений. Составим
определитель Вронского
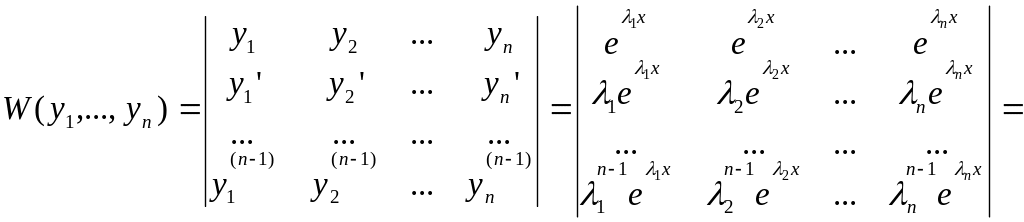
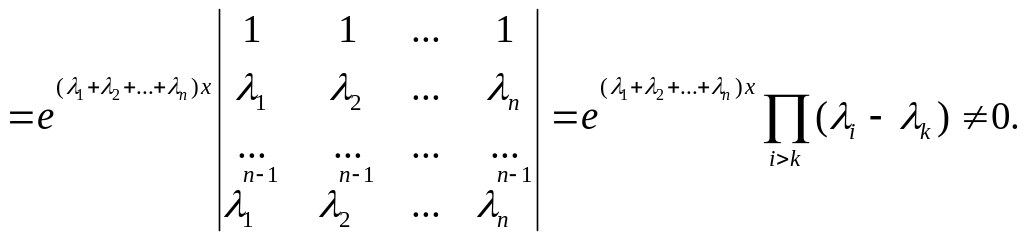
В наших расчетах встретился определитель Вандермонда
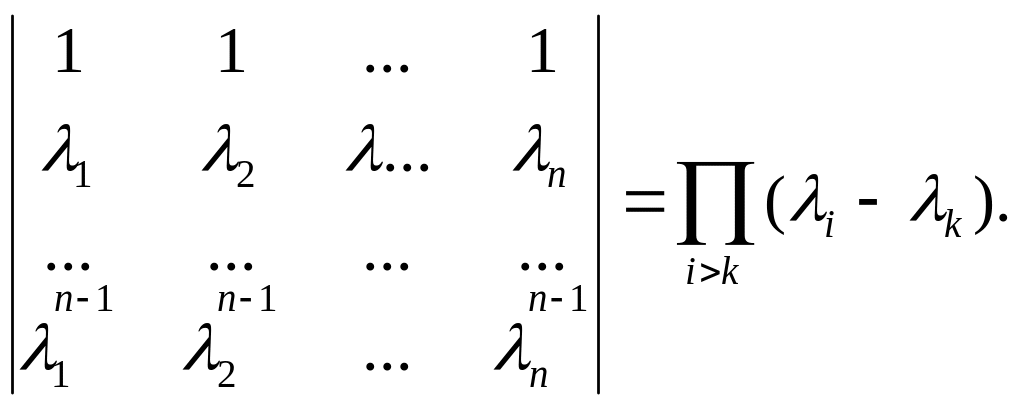
равный произведениям
всевозможных попарных разностей чисел
![]() Поскольку определитель Вронского
отличен от нуля, найденная система
решений фундаментальна, и общее решение
линейного однородного ду в случае
простых корней имеет вид:
Поскольку определитель Вронского
отличен от нуля, найденная система
решений фундаментальна, и общее решение
линейного однородного ду в случае
простых корней имеет вид:
![]()
Таким образом,
для построения общего решения (12)
достаточно найти корни характеристического
многочлена, т.е. решить уравнения
![]() Если среди корней
Если среди корней
![]() встречаются комплексные, то выделяют
действительное решение. Делается это
следующим образом. Пусть
встречаются комплексные, то выделяют
действительное решение. Делается это
следующим образом. Пусть
![]() -
корень характеристического уравнения.
Так как коэффициенты многочлена
действительны, то имеется сопряженный
корень
-
корень характеристического уравнения.
Так как коэффициенты многочлена
действительны, то имеется сопряженный
корень
![]() .Таким
образом, имеем два комплексных решения
.Таким
образом, имеем два комплексных решения
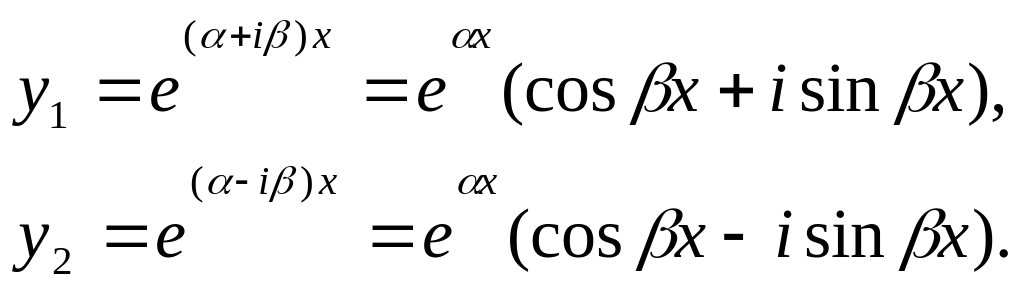
Комбинируя их,
легко получить два действительных
решения
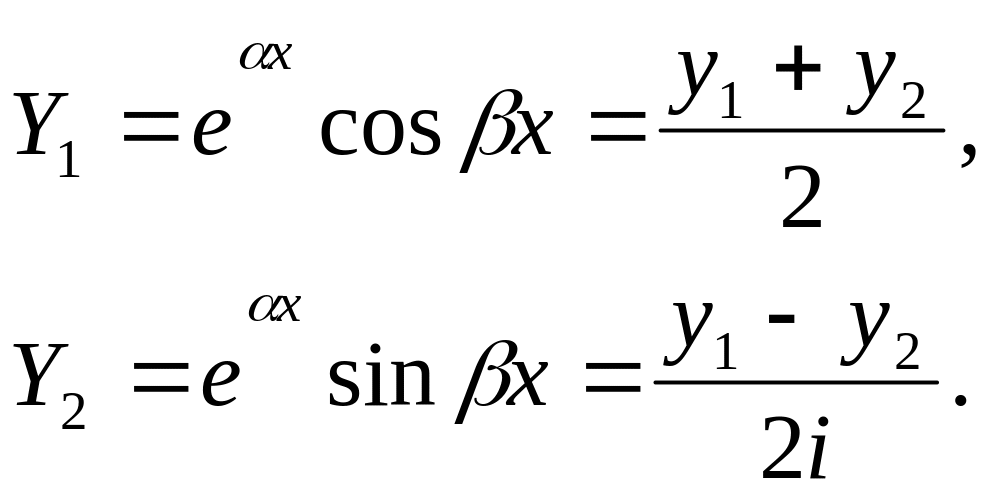
Проверим, что
найденные решения линейно независимы.
Для этого составим определитель матрицы
перехода
![]()
Тогда из линейной
зависимости решений
![]() вытекает линейная независимость решений
вытекает линейная независимость решений
![]() .
.
В случае, когда
имеется несколько комплексных корней,
определитель матрицы перехода

В результате мы можем получить только линейно независимые действительные решения.
Билет №34
Построение фундаментальной системы решений линейного однородного уравнения с постоянными коэффициентами в случае кратных корней характеристического многочлена (действительных и комплексных).
Пусть характеристический
многочлен
![]() имеет кратные корни: корень 1
кратности m1,
корень 2
кратности m2
, …., кореньk
кратности mk
, причем
имеет кратные корни: корень 1
кратности m1,
корень 2
кратности m2
, …., кореньk
кратности mk
, причем
![]() В
этом случае операторный многочлен M(D)
может быть разложен на следующие
множители:
В
этом случае операторный многочлен M(D)
может быть разложен на следующие
множители:
![]() а дифференциальное уравнение
а дифференциальное уравнение
![]() распадается на k
уравнений
распадается на k
уравнений
![]() Мы уже знаем, что решением этого уравнения
является функция
Мы уже знаем, что решением этого уравнения
является функция
![]() Но всего таких решений k<n
Нам не хватает (n-k)
решений для построения фундаментальной
системы. Как найти дополнительные
условия ? Введем сначала вспомогательное
операторное соотношение, называемое
формулой смещения
Но всего таких решений k<n
Нам не хватает (n-k)
решений для построения фундаментальной
системы. Как найти дополнительные
условия ? Введем сначала вспомогательное
операторное соотношение, называемое
формулой смещения
![]() Подставим в левую часть выражения
операторного многочлена
Подставим в левую часть выражения
операторного многочлена
![]() Тогда,
Тогда,
![]() Применим
формулу Лейбница для производной от
произведения функций
Применим
формулу Лейбница для производной от
произведения функций![]()
![]()
Вернемся к уравнению
(1). Будем искать его решение в виде
![]() Тогда,
Тогда,
![]() и применяя формулу смещения, имеем:
и применяя формулу смещения, имеем:
![]()
Или
![]()
Решением получившегося
уравнения является произвольный полином
степени
![]() т.е.
т.е.
![]()
Окончательный вид
решения уравнения (1) таков
![]()
Как получить отсюда линейно независимые решения ?
Будем полагать
поочередно:
![]() ,
остальные – нули;
,
остальные – нули;
![]() ,
остальные нули;…;
,
остальные нули;…;
![]() ,
остальные – нули. В результате получим
,
остальные – нули. В результате получим
![]() решений
вида
решений
вида
![]()
Соответствующих
кратности корня
![]() характеристического
многочлена. Сирии решений вида (3)
получается для всех остальных корней
, так что общее число построенных решений
равно
характеристического
многочлена. Сирии решений вида (3)
получается для всех остальных корней
, так что общее число построенных решений
равно
Покажем, что
построенная система решений фундаментальна.
Предположим противное, т.е. что система
решений линейно зависима. Это означает,
что существует набор действительных
постоянных
![]() (не все из которых нули), для которого
(не все из которых нули), для которого
![]()
Или
![]()
Покажем, что отсюда
вытекает равенство нулю всех многочленов
![]()
Снова применим
прием от противного. Пусть хотя бы у
одного из многочленов не все коэффициенты
являются нулями, например у
![]() отличен
от нуля коэффициент при старшей степени
отличен
от нуля коэффициент при старшей степени
![]() Разделим
тождество (4) на
Разделим
тождество (4) на
![]()
![]()
И продифференцируем
его
![]() раз
для того, чтобы исчез многочлен
раз
для того, чтобы исчез многочлен
![]() Поскольку
Поскольку
![]()
То в силу условий
![]() и
и
![]() в
квадратных скобках получается многочлен
той же степени, что и
.В
результате, после дифференцирования
раз придем к
в
квадратных скобках получается многочлен
той же степени, что и
.В
результате, после дифференцирования
раз придем к
![]()
Многочленов стало
на один меньше. Разделим теперь тождество
на
![]() и
продифференцируем его
и
продифференцируем его
![]() раз для того, чтобы исчез многочлен
раз для того, чтобы исчез многочлен
![]() В результате получим
В результате получим
![]() слагаемых.
И т.д. В конце этой процедуры придем к
тождеству вида
слагаемых.
И т.д. В конце этой процедуры придем к
тождеству вида
![]()
Из него следует,
что
![]() ,
а значит все коэффициенты многочлена
,
а значит все коэффициенты многочлена
![]() обращаются в нуль. В том числе и коэффициент
при старшей степени, который совпадает
с аналогичным коэффициентом
обращаются в нуль. В том числе и коэффициент
при старшей степени, который совпадает
с аналогичным коэффициентом
![]() исходного
полинома
исходного
полинома
![]() Мы
пришли к противоречию, поскольку полагали
этот коэффициент отличным от нуля.
Мы
пришли к противоречию, поскольку полагали
этот коэффициент отличным от нуля.
Таким образом все
полиномы в тождестве (4) равны нулю.
Следовательно, обращаются в нуль и все
коэффициенты
![]() Получили
еще одно противоречие, которое и
доказывает фундаментальность построенной
системы решений (3)
Получили
еще одно противоречие, которое и
доказывает фундаментальность построенной
системы решений (3)
Итак, в случае
кратных корней фундаментальная система
решений имеет вид:
![]()
Общее решение линейного однородного уравнения является линейной суперпозицией этих решений.
Остановимся и здесь
на способе выделения действительных
решений в случае комплексных корней
![]() .
Пусть комплексный корень
.
Пусть комплексный корень
![]() имеет кратность
имеет кратность
![]() .
Тогда, как мы знаем , существует
комплексно-сопряженный корень
.
Тогда, как мы знаем , существует
комплексно-сопряженный корень
![]() той же кратности. Корню
той же кратности. Корню
![]() соответствует решения вида
соответствует решения вида
![]()
Корню
![]() соответствуют решения
соответствуют решения
![]()
всего таких решений
2
.
Из них почленным сложением и вычитанием,
т.е. невырожденным преобразованием,
можно получить следующие
![]() линейно независимых действительных
решений :
линейно независимых действительных
решений :![]() Билет №35.
Билет №35.
Отыскание частного решения линейного неоднородного уравнения с постоянными коэффициентами методом неопределённых коэффициентов (подбором).
Метод неопределённых
коэффициентов можно использовать, если
правая часть линейного дифференциального
уравнения квазиполином. Функция
вида
![]() ,
где
,
где
![]() -
полином, а
-
полином, а
![]() -
некоторая, вообще говоря, комплексная
постоянная, носит названия квазиполинома.
-
некоторая, вообще говоря, комплексная
постоянная, носит названия квазиполинома.
Отметим основные свойства квазиполиномов.
Сумма двух квазиполиномов с одинаковыми показательными функциями есть снова квазиполином:
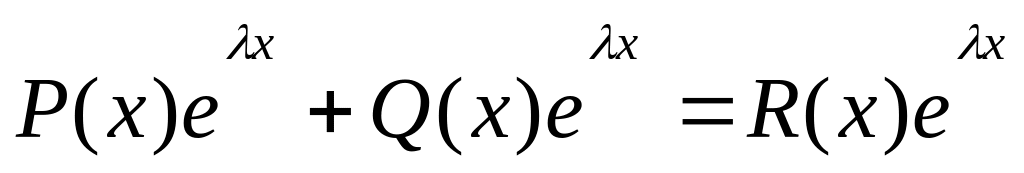
Произведение двух квазиполиномов дает снова квазиполином:
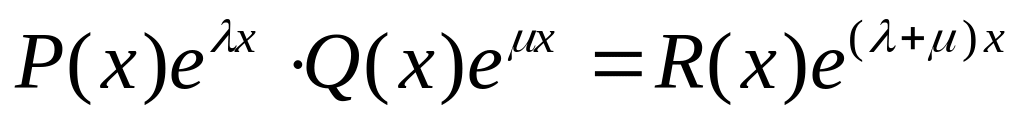
Производная от квазиполинома – квазиполином
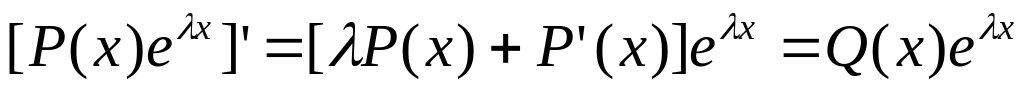
После действий операторного многочлена на квазиполином – получается снова квазиполином

Рассмотрим линейное неоднородное дифференциальное уравнение с квазиполиномом в правой части
![]() (1).
Здесь ,
вообще говоря, некоторое комплексное
число, а коэффициенты многочлена
(1).
Здесь ,
вообще говоря, некоторое комплексное
число, а коэффициенты многочлена
![]() действительны.
действительны.
![]() …
…![]()
Теорема. Уравнение
(1)
имеет частное решение вида:
![]() (2),
где
(2),
где
![]() - многочлен той же степени, что и
:
- многочлен той же степени, что и
:
![]() …
…![]() .
.
Если
- не корень характеристического
многочлена, т.е.
![]() ,
то
,
то
![]() ;
если
- корень характеристического многочлена,
т.е.
;
если
- корень характеристического многочлена,
т.е.
![]() ,
то
,
то
![]() - его кратность .
- его кратность .
Доказательство: докажем, что (2) – решение (1). Рассмотрим равенство
![]()
Применим в левой
части формулу смещения:
![]()
и сократим на
![]() :
:
![]() (3).
Теперь нам осталось показать, что можно
подобрать коэффициенты многочлена
с0,
с1,
… сr
так, что бы выполнялось равенство (3).
Поскольку
- m-кратный
корень многочлена
(3).
Теперь нам осталось показать, что можно
подобрать коэффициенты многочлена
с0,
с1,
… сr
так, что бы выполнялось равенство (3).
Поскольку
- m-кратный
корень многочлена
![]() :
,
операторный многочлен
:
,
операторный многочлен
![]() допускает представления в виде:
допускает представления в виде:
![]() (4), где
(4), где
![]() (
,
если
- не корень
).
Подставляя (4) в (3), находим:
(
,
если
- не корень
).
Подставляя (4) в (3), находим:
![]() или
или
![]() (5).
Представим оператор
(5).
Представим оператор
![]() в виде:
в виде:
![]() .
Тогда,
.
Тогда,
![]() (6)
(6)
Определим старший
полиномиальный член слева и приравняем
его подобному справа в силу произвольности
:
![]() .
Поскольку
.
Поскольку
![]() ,
то коэффициент с0
находиться однозначно:
,
то коэффициент с0
находиться однозначно:
![]() .
В результате уравнение (6)
примет вид:
.
В результате уравнение (6)
примет вид:
![]() (7).
Уравнения (5)
и (7)
имеют одинаковую структуру, но в (7)
степень полинома справа стала меньше
на единицу. Поэтому, аналогичным способом
найдем с1.
И т.д. Аналогично можно однозначно найти
остальные коэффициенты с2,
… сr.
Таким образом, решение вида (2) уравнения
(1) существует.
(7).
Уравнения (5)
и (7)
имеют одинаковую структуру, но в (7)
степень полинома справа стала меньше
на единицу. Поэтому, аналогичным способом
найдем с1.
И т.д. Аналогично можно однозначно найти
остальные коэффициенты с2,
… сr.
Таким образом, решение вида (2) уравнения
(1) существует.
Пример.
Дано неоднородное уравнение второго
порядка:
![]() .
.
Составим
характеристическое уравнение:
![]() .
Оно имеет один двукратный корень
.
Оно имеет один двукратный корень
![]() ,
т.е.
,
т.е.
![]() .
Из правой части уравнения определяем
значение =1.
Оно совпадает с корнем характеристического
многочлена, поэтому частное решение
неоднородного уравнения ищем в виде:
.
Из правой части уравнения определяем
значение =1.
Оно совпадает с корнем характеристического
многочлена, поэтому частное решение
неоднородного уравнения ищем в виде:
![]() ,
где коэффициенты с0,
с1
- неизвестны. Для их определения подставим
решение в исходное уравнение и применим
формулу сдвига:
,
где коэффициенты с0,
с1
- неизвестны. Для их определения подставим
решение в исходное уравнение и применим
формулу сдвига:
![]() Отсюда,
пользуясь произвольностью x,
определяем коэффициенты: с0=1/6,
с1=0.
Таким образом, частное решение
неоднородного уравнения таково:
Отсюда,
пользуясь произвольностью x,
определяем коэффициенты: с0=1/6,
с1=0.
Таким образом, частное решение
неоднородного уравнения таково:
![]() .
.
Билет №36
Оператор дифференцирования. Операторные многочлены и их свойства. Действие оператора на простейшие функции. Формула смещения.
Перейдем к анализу линейного однородного дифференциального уравнения n –го порядка с постоянными коэффициентами Где . Попытаемся найти фундамент. систему решений уравнения (8).
Введём оператор дифференцирования D: y’=Dy. Тогда y’’=(y’)’=D(Dy)=D2y, … y(n)=Dny. Уравнение
(8) при этом примет вид Dny+a1Dn-1y+…+ an-1Dy+ any=0 или
(Dn+a1Dn-1+…+ an-1D+an)y=0 Многочлен, стоящий перед функцией y, является многочленом от оператора дифференцирования и носит названия операторного многочлена M(D): Уравнение (8) принимает компактный вид: M(D)y=0.
Отметим основные свойства операторных многочленов.
Закон сложения (ассоциативность):
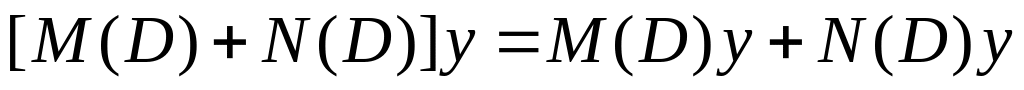
Под умножением операторных многочленов понимается их последовательное применение
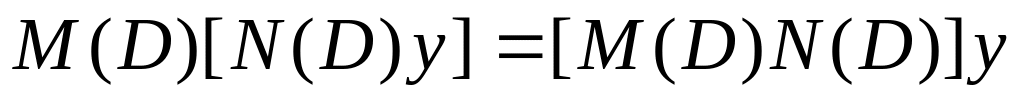 Отсюда
Отсюда
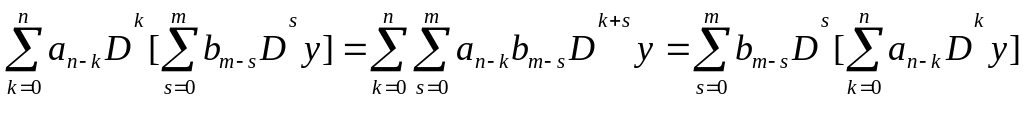
Следовательно, верен переместительный закон:
Поскольку M(D) – дифференциальный оператор, то
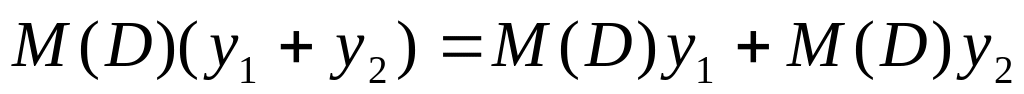
Справедлив дистрибутивный закон
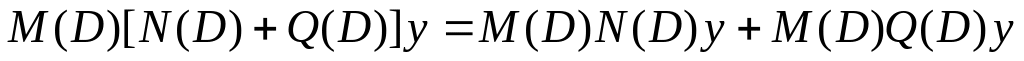
Свойства 1-4 показывают, что для операторных многочленов справедливы все теоремы алгебры. Отсюда следует еще одно свойство.
5. Операторный многочлен можно разложить на множители. Введем характеристический многочлен
Этот многочлен имеет n корней и представим по теореме алгебры в виде Значит,
Формула смещения.
Подставим в левую
часть выражения операторного многочлена
![]()
Тогда, Применим формулу Лейбница для производной от произведения функций Действие оператора на простейшие функции.
1)
![]()
2)
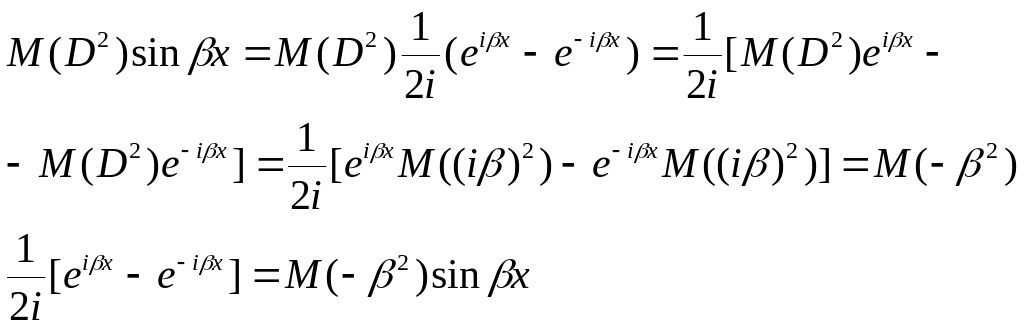
3)
![]() (Доказательство
аналогичное)
(Доказательство
аналогичное)
Билет №37
Операторный метод отыскания частного решения линейного неоднородного уравнения с постоянными коэффициентами. Понятие обратного оператора, его свойства. Действие обратного оператора на простейшие функции. Формула смещения. Разложение обратного оператора на простейшие дроби.
Обратный оператор.
Запишем исследуемое линейное неоднородное
дифференциальное уравнение n-ого
порядка в операторной форме:
![]() (8). Если отсюда формально найти
,
то получим:
(8). Если отсюда формально найти
,
то получим:
![]() (9). Оператор
(9). Оператор
![]() ,
стоящий в (9), называют обратным операторному
многочлену
или просто обратным
оператором.
Если мы изучим свойства обратного
оператора, то это позволит нам достаточно
просто находить частное решение
неоднородного уравнения (8).
,
стоящий в (9), называют обратным операторному
многочлену
или просто обратным
оператором.
Если мы изучим свойства обратного
оператора, то это позволит нам достаточно
просто находить частное решение
неоднородного уравнения (8).
Свойства 1/M(D).
Подставляя (9) в (8), мы должны получить тождество, так как (9) – решение уравнения (8). Значит,
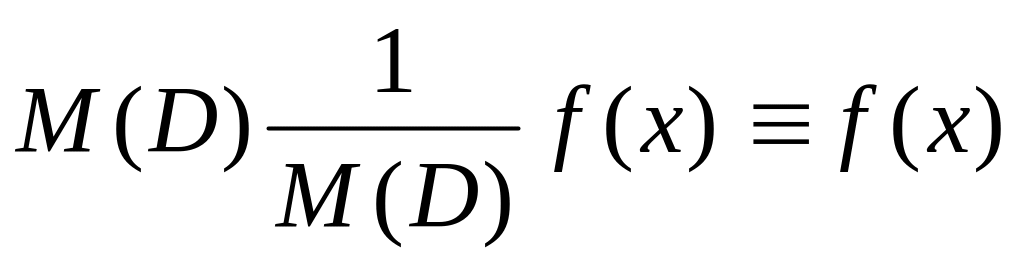 .
Поскольку
.
Поскольку
 может быть любой, имеем:
может быть любой, имеем:
![]() (10).
(10).
Рассмотрим уравнение:
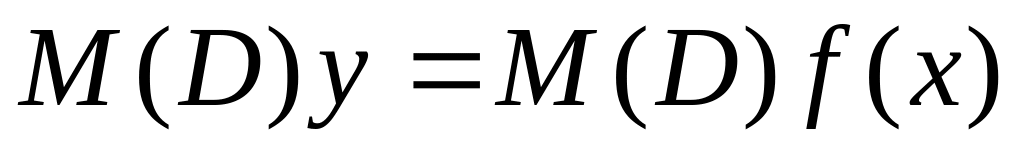 (11). Тогда ясно, что
(11). Тогда ясно, что
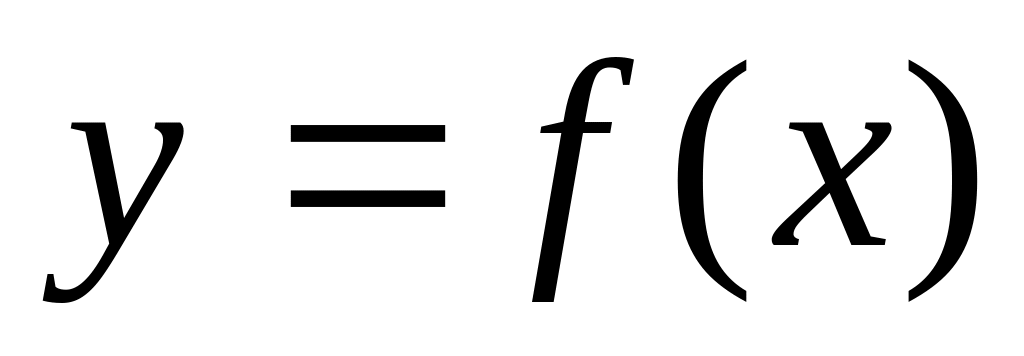 является решением данного уравнения,
но не единственным. Функции вида
является решением данного уравнения,
но не единственным. Функции вида
 ,
где
,
где
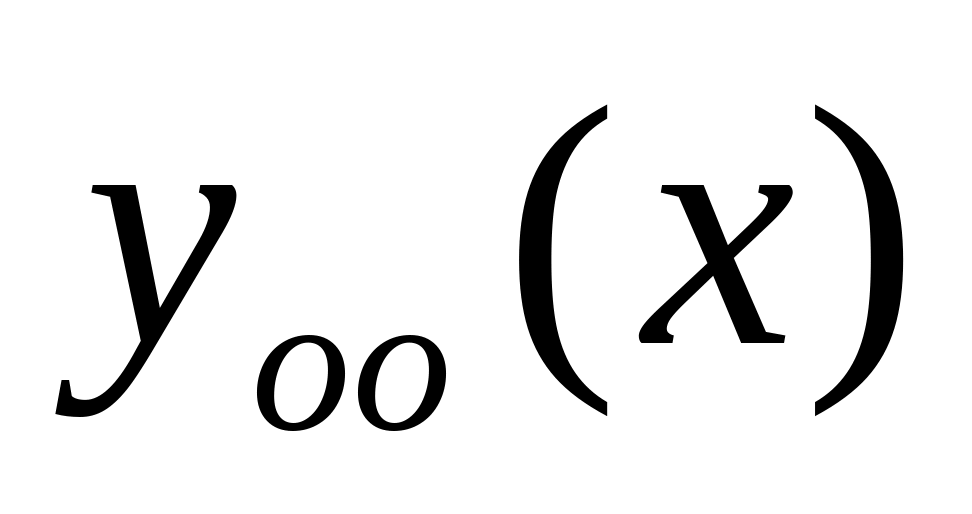 - общее решение однородного уравнения
- общее решение однородного уравнения
 ,
также являются решениями. Из (11) находим:
,
также являются решениями. Из (11) находим:
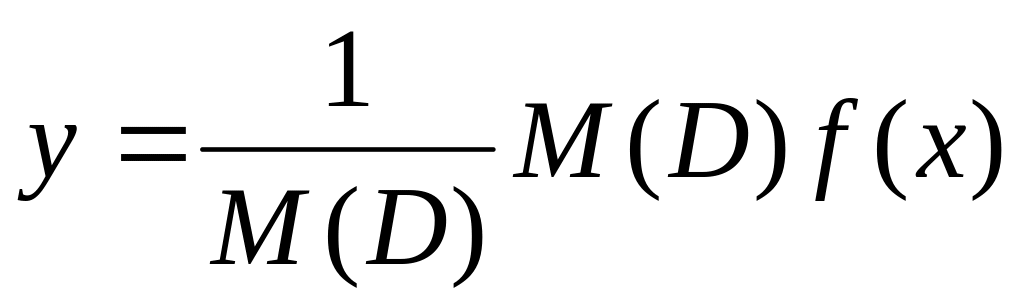 .
Значит равенство
.
Значит равенство
![]() (12) справедливо
с точностью до решения линейного
однородного уравнения. Вывод:
Обратный оператор (9) находит решение
уравнения (8) с точностью до решения
линейного однородного уравнения. Из
(12) получаем второе свойство, когда
прямой и обратный операторы действуют
в другом порядке:
(12) справедливо
с точностью до решения линейного
однородного уравнения. Вывод:
Обратный оператор (9) находит решение
уравнения (8) с точностью до решения
линейного однородного уравнения. Из
(12) получаем второе свойство, когда
прямой и обратный операторы действуют
в другом порядке:
![]() (13). В соответствии с (10), (13) прямой
и обратный операторы можно менять
местами и сокращать.
(13). В соответствии с (10), (13) прямой
и обратный операторы можно менять
местами и сокращать.
Рассмотрим уравнение первого порядка:
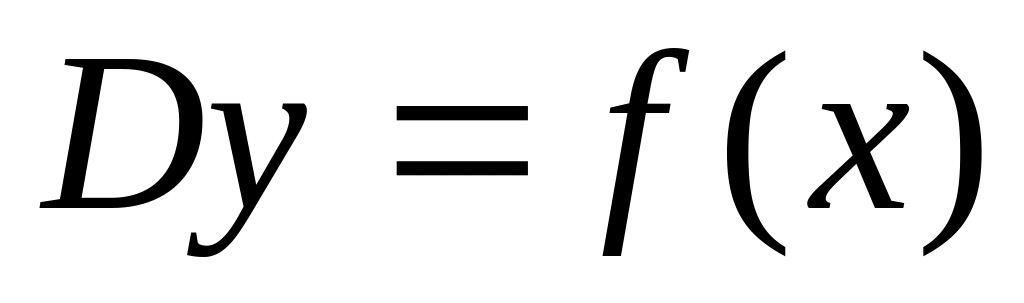 .
Отсюда,
.
Отсюда,
 .
С другой стороны,
.
С другой стороны,
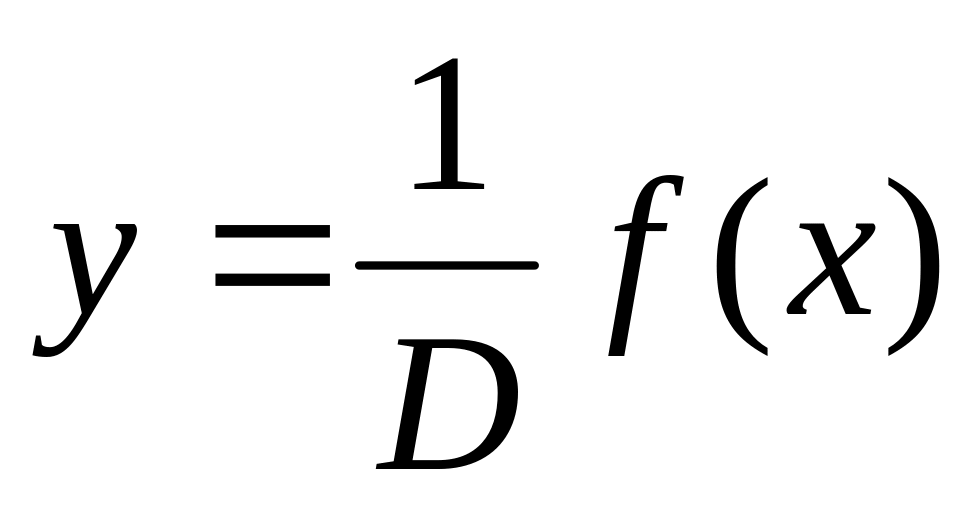 .
Сопоставление показывает, что оператор
.
Сопоставление показывает, что оператор
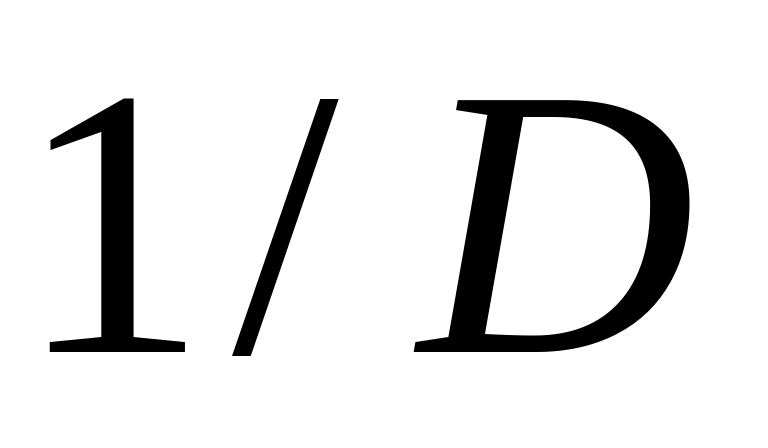 является оператором интегрирования:
является оператором интегрирования:
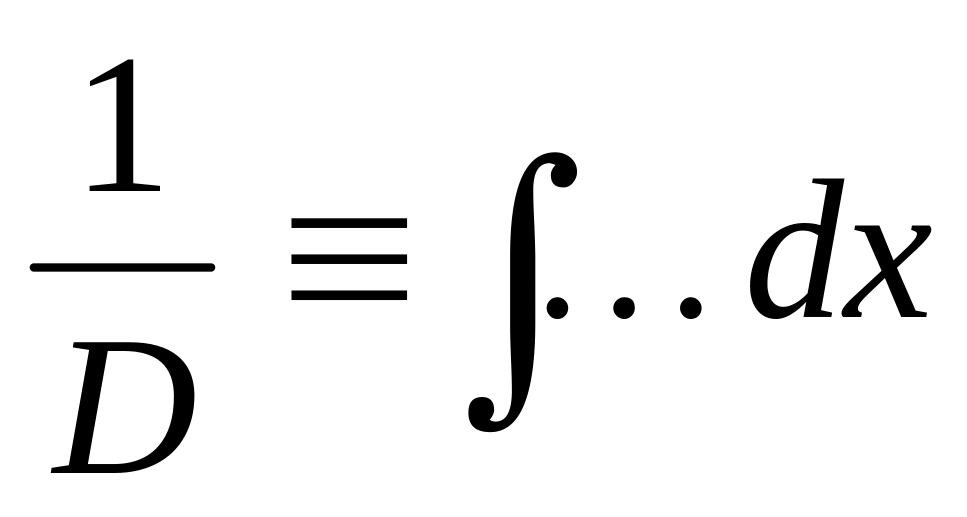 (14). Определим действие умножения
произвольного операторного многочлена
на обратный оператор:
(14). Определим действие умножения
произвольного операторного многочлена
на обратный оператор:
![]() .
Аналогично наоборот:
.
Аналогично наоборот:
![]() .
Докажем, что эти операции обладают
переместительным свойством:
.
Докажем, что эти операции обладают
переместительным свойством:
![]() (15). Введем обозначение:
(15). Введем обозначение:
![]() .
.
Тогда,
![]() .
Отсюда
.
Отсюда
![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.
Справедливо еще одно равенство для обратного оператора
![]() (16). Это
равенство следует из принципа суперпозиции
для линейного неоднородного уравнения:
сумма частных решений неоднородного
уравнения с
(16). Это
равенство следует из принципа суперпозиции
для линейного неоднородного уравнения:
сумма частных решений неоднородного
уравнения с
![]() и
и
![]() в правой части дает частное решение
неоднородного уравнения с суммарной
правой частью
в правой части дает частное решение
неоднородного уравнения с суммарной
правой частью
![]() .
.
Определение сложения обратных операторов:
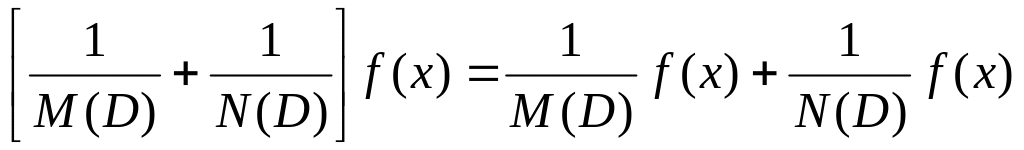 .
Они складываются по типу дробей.
Умножение для обратных операторов
определяют как:
.
Они складываются по типу дробей.
Умножение для обратных операторов
определяют как:
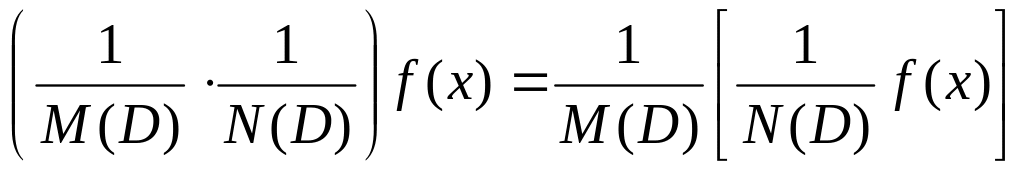 .
Проверим, выполняются ли переместительное
свойство для обратных операторов.
.
Проверим, выполняются ли переместительное
свойство для обратных операторов.
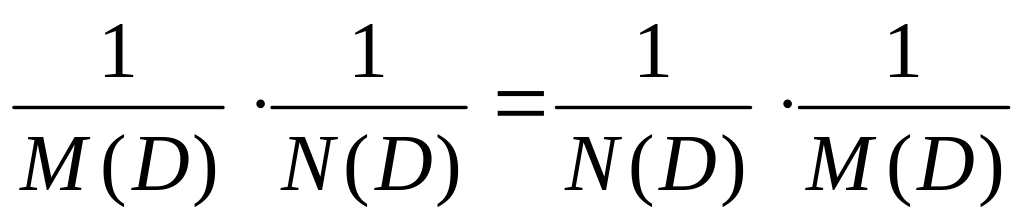 ?
Введем обозначение:
?
Введем обозначение:
![]() .
Тогда,
.
Тогда,
![]()
![]() ,
и свойство доказано. Таким образом
,
и свойство доказано. Таким образом
(17)
В силу доказанных равенств на обратный оператор можно распространить все свойства алгебраических дробей. В частности, операторная дробь как и алгебраическая должна раскладываться на простейшие дроби. Пусть характеристический многочлен имеет корни:
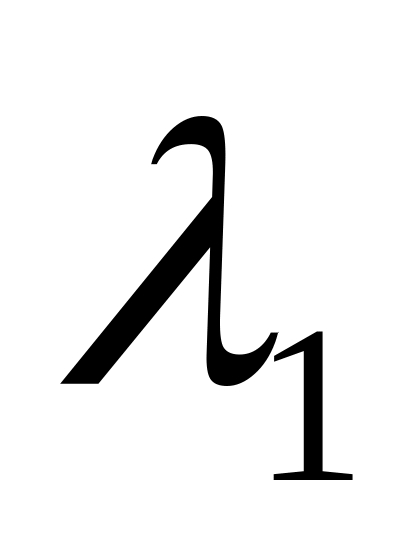 кратности
;…;
кратности
;…;
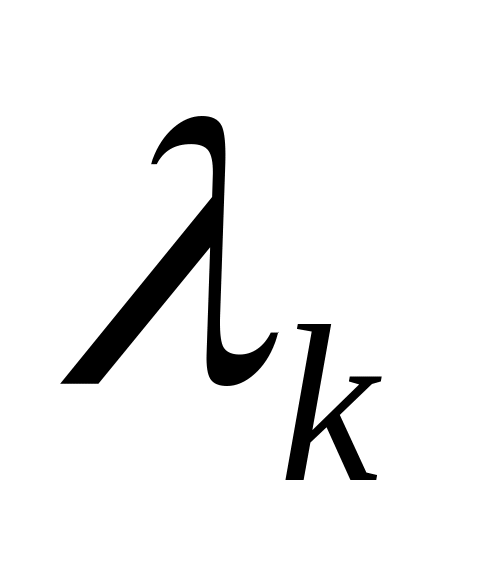 кратности
кратности
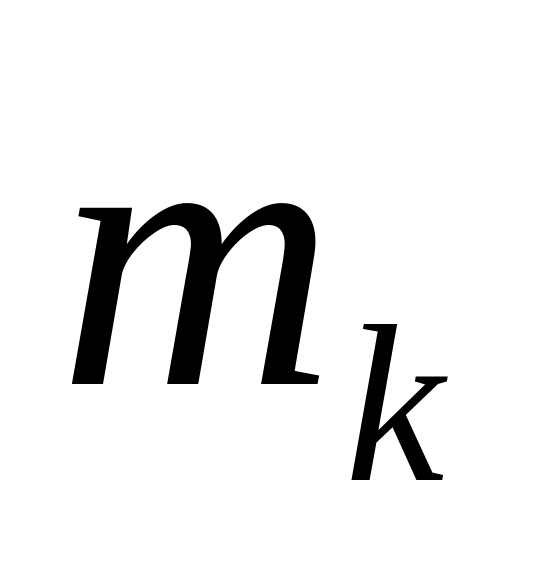 .
Тогда,
.
Тогда,
![]() …
…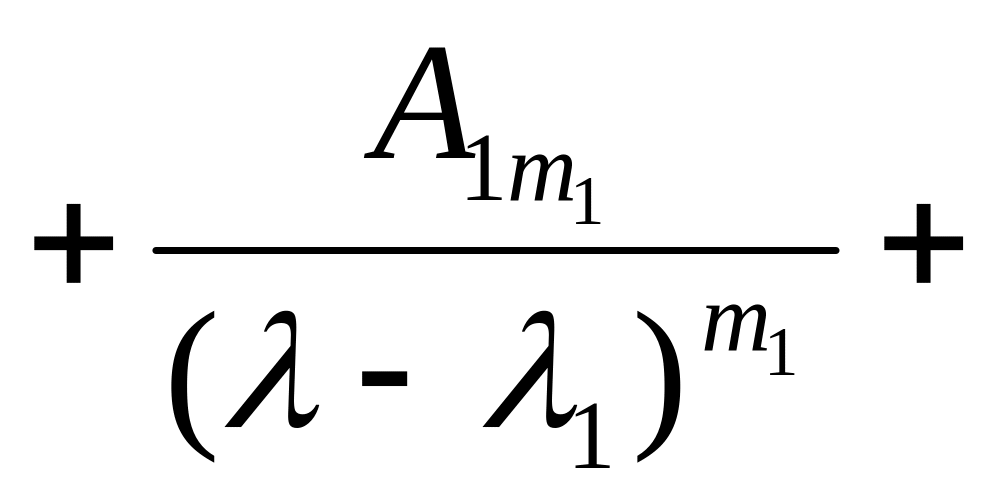 …
…![]() …
… .
В результате,
.
В результате,
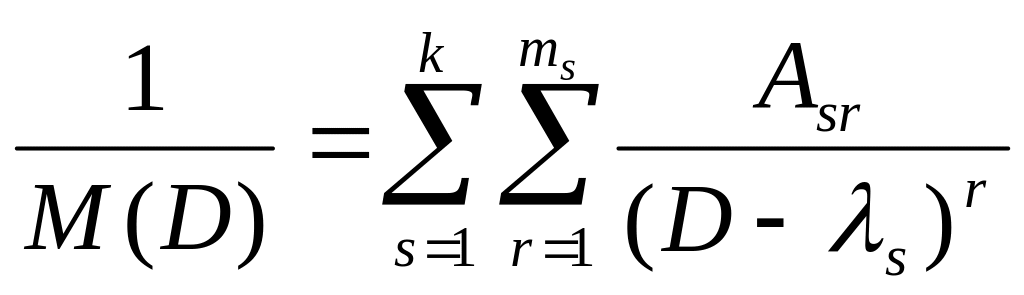 (18). Важное
соотношение (18) позволяет свести действие
обратного оператора к сумме действий
простейших операторов.
(18). Важное
соотношение (18) позволяет свести действие
обратного оператора к сумме действий
простейших операторов.
Билет №41
Теорема об эквивалентности нормальной системы n дифференциальных уравнений и одного уравнения n-го порядка, разрешенного относительно старшей производной. Метод исключения.
Рассмотрим нормальную систему дифференциальных уравнений: dy1/dx=f1(x,y1,........yn), …… ........., yn/dx=fn(x,y1,..........,yn) (1). Предположим, что функции f1,..............,fn дифференцируемы неограниченное число раз. Общим методом решения системы (1) является метод исключения. Докажем теорему. Теорема. Об эквивалентности нормальной системы одному дифференциальному уравнению.
Нормальная система
n
дифференциальных уравнений эквивалентна
одному дифференциальному уравнению
n-го
порядка при условии дифференцируемости
правых частей f1,
f2
............fn.
Доказательство:
будем исключать
переменные y1,y2,..........yn
и строить дифференциальное уравнение
относительно функции y1.
Как известно, решением системы (1) является
система функций: y1=1(x).........,yn=n(x).
Подставляя ее в (1). получаем тождества:
d1(x)/dxf1(x,
1(x),........,
n(x))=f1~,
……… ........, dn(x)/dxfn(x,
1(x),...........,
n(x))=fn~
(2). Продифференцируем по х первое
множество системы (2):d21/dx2=f~1/dx+![]() (
f~1/yk)*(dk/dx)=
f~1/dx+
(f~1/yk)*(fk~)=F2(x,1(x),....,n(x))=F2~.
Далее находим еще одну производную
d31/dx3=
F2~/x
+
F2~/yk*fk~F3(x,1(x),........,
,n(x))=F3~.
Итак далее. Наконец, dn1/dxn=Fn-1~/x+
Fn
-1~/yk*fk~Fn(x,1(x),........,
,n(x))=Fn~.
В итоге мы получили новую систему
тождеств. По образцу этих тождеств
составим следующую систему уравнений:
dy1/dx=f1(x,y1,y2,......,yn),
d2y1/dx2=F2(x,y1,y2,......,yn),......
..........,dn-1y1/dxn-1=Fn-1(x,y1,y2,......,yn)
(3). Добавим к системе (3) отдельное
уравнение: dny1/dxn=Fn(x,y1,y2,......,yn)
(4). Будем рассматривать
(
f~1/yk)*(dk/dx)=
f~1/dx+
(f~1/yk)*(fk~)=F2(x,1(x),....,n(x))=F2~.
Далее находим еще одну производную
d31/dx3=
F2~/x
+
F2~/yk*fk~F3(x,1(x),........,
,n(x))=F3~.
Итак далее. Наконец, dn1/dxn=Fn-1~/x+
Fn
-1~/yk*fk~Fn(x,1(x),........,
,n(x))=Fn~.
В итоге мы получили новую систему
тождеств. По образцу этих тождеств
составим следующую систему уравнений:
dy1/dx=f1(x,y1,y2,......,yn),
d2y1/dx2=F2(x,y1,y2,......,yn),......
..........,dn-1y1/dxn-1=Fn-1(x,y1,y2,......,yn)
(3). Добавим к системе (3) отдельное
уравнение: dny1/dxn=Fn(x,y1,y2,......,yn)
(4). Будем рассматривать
переменные y2,......,yn системы (3) в качестве неизвестных. Тогда систему (3) можно разрешить
относительно этих переменных, если якобиан: D(f1,F2,..........,Fn-1)/D(y2,......,yn)0 (5). Если условие (5)
выполняется, то получим: y2=2(x,y1,y1/,.........,y1(n-1)),.......... ........, yn=n(x,y1,y1/,.........,y1(n-1)) (6).
Учитывая, что функция 2,.....,n являются решениями системы (3), и ранее установленные тождества
(2), имеем: 2(x,1(x),1/(x),......., 1n-1(x)) 2(x), ...... ......…, n(x,1(x),1/(x),......., 1n-1(x)) n(x) (7).
Подставляя выражения (6) в уравнение (4), придем окончательно к: dny1/dxn=Fn(x,y1,2,.....,n) =
= ( x,y1,y1/,.........,y1(n-1)) (8). Составленное уравнение (8) и будет искомым уравнением. Проверим, что
функция 1(x) является решением уравнения (8). Подстановка 1(x) в левую и правую части уравнения
(8) с учетом тождеств (7) дает: dn1/dxn=Fn(x, 1, 2,....., n)=Fn~, что совпадает с последним из ранее
полученных тождеств. Проведем теперь доказательство в обратную сторону. Покажем, что если
известно какое-либо решение уравнения (8), то можно без дополнительного интегрирования получить
решение нормальной системы (1). Пусть y1=1(x) – решение дифференциального уравнения (8). Для
того чтобы построить решение системы необходимо найти функции y1, y2 ..........yn. Составим систему:
d1/dx=f1(x,1,y2,.....,yn); d21/dx2=F2(x,1,y2,.....,yn); ......... ......; dn-11/dxn-1=Fn-1(x,1,y2,.....,yn) (9).Эта
алгебраическая система уравнений с неизвестными y2 ..........yn очень похожа на (3). В силу условия (5)
эта система разрешима относительно y2 ..........yn, и решением ее будут функции y2=2(x),...., yn=n(x).
Однако неизвестно, является ли найденная система функций вместе с 1(x) решением нормальной
системы (1)? Если 2,.....,n подставить в (9), то получим тождества: d1/dxf1(x, 1, 2,......, n),
d21/dx2F2(x, 1, 2,......, n),........... ..........., dn-11/dxn-1Fn-1(x, 1, 2,......, n) (10). В тоже время,
поскольку функция 1(х) является решением уравнения (8), имеет место тождество: dn1/dxn=
=Fn(x, 1, 2,......, n) (11). Продифференцируем по х обе части первого из тождеств (10):
d21/dx2f1/x+ (f1/yk)*( dk/dx) (12). Записывая второе из тождеств (10) в развернутой
форме, находим: d21/dx2f1/x+ (f1/yk)*fk (13). Вычитая почленно (13) и (12), имеем:
(f1/yk)*(dk/dx- fk)0
В соответствии с
первым из тождеств (10): d1/dx=f1.
Поэтому,
![]() (f1/yk)(
dk/dx-
fk)0
(14).
(f1/yk)(
dk/dx-
fk)0
(14).
Продифференцируем далее по х второе из тождеств (10): d31/dx3= F2/x+ (F2/yk)*(dk/dx),
и запишем третье тождество в развернутом виде: d31/dx3= F2/x+ (F2/yk)*fk.
По членное вычитание и учет того, что d1/dx=f1 дает: (F2/yk)( dk/dx- fk)0 (15). Аналогичным
образом поступаем до (n-1)-го тождества. Дифференцирование последнего из тождеств (10) и
вычитание из него тождества (11), записанного в развернутой форме, приводит к:
(Fn-1/yk)( dk/dx- fk)0 (16). В итоге мы получили систему тождеств (14)-(16), где
неизвестными являются разности (dk/dx-fk). Определителем этой однородной системы является
якобиан (5), отличный от нуля при любом х. Следовательно, система (14)-(16) при всех х имеет только
нулевое решение, т.е. dk/dxfk, k = 2,3,............,n. К тому же d1/dxf1. Значит, найденная система
функций является решением нормальной системы (1).
Замечание. В процессе доказательства теоремы использовано условие отличности от нуля якобиана (5).
Если якобиан везде равен нулю, то можно попытаться построить уравнение для переменной у2. И т.д.
Может, однако, оказаться, что все якобианы типа (5) относительно у1,у2......,уn обращаются в нуль.
Значит, методом исключения нельзя построить одно дифференциальное уравнение n-го порядка. В
этом случае нормальная система (1) распадается на несколько подситсем. Например,
dy1/dx=f1(x,y1,y2); dy2/dx=f2(x,y1,y2); dy3/dx=f3(x,y3,y4); dy4/dx=f4(x,y3,y4).
Каждую из таких подсистем можно анализировать отдельно, т.е. строить для нее дифференциальное
уравнение соответствующего порядка.
Билет №42
Теоремы о непрерывной зависимости и о дифференцируемости решения нормальной системы по начальным условиям и по параметру (без доказательства). Определение первого интеграла для нормальной системы дифференциальных уравнений. Независимость интегралов. Существование n независимых первых интегралов, как следствие теоремы о дифференцируемости решений нормальной системы по начальным условиям.
Линейные системы дифференциальных уравнений.
Линейной системой дифференциальных уравнение называется система уравнений вида:
dy1/dx=a11(x)y1+......+a1n(x)yn+f1(x); .......... ......... ;dyn/dx=an1(x)y1+......+ann(x)yn+fn(x) (17). Входящие в
(17) функции aik(x) и fi(x) предполагаются непрерывными на отрезке a,b. Это обеспечивает, как мы
видели ранее, выполнение условий теоремы существования и единственности решения в области
axb, -y1<,.......,-yn<. Таким образом, система (17) имеет единственное решение при любом
начальном условии (x0,y10,.....,yn0), где a<x0<b, -y10<........,-yn0<. Очень часто систему (17)
записывают в
векторной форме. Если ввести матричную
функцию: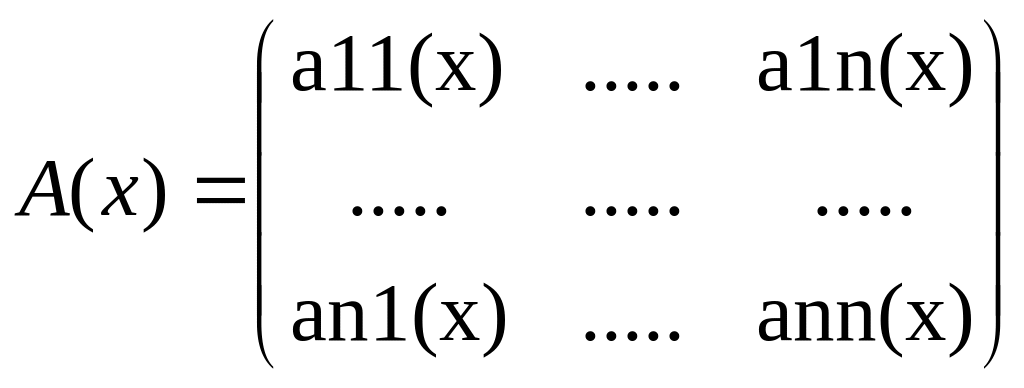
И вектор – функции:
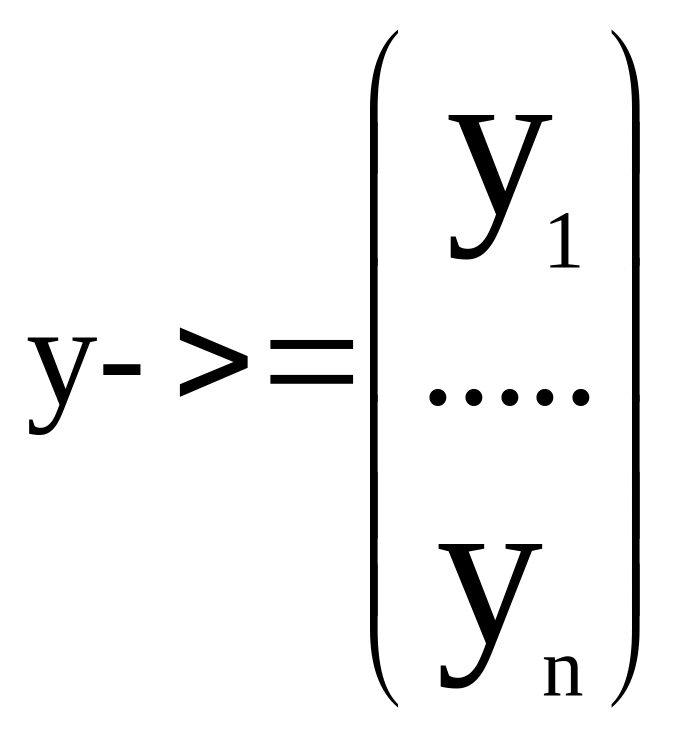
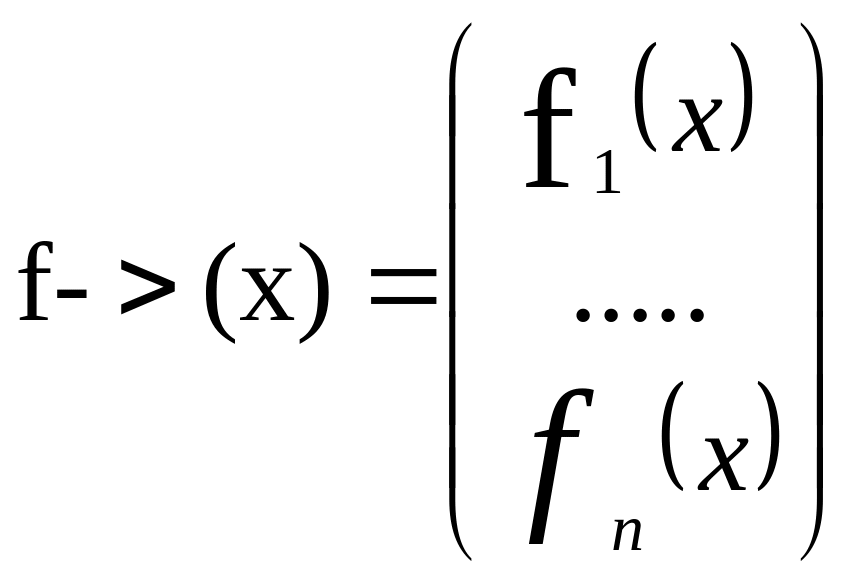 ,
то систему (17) можно переписать как
,
то систему (17) можно переписать как
dy->/dx=A(x)y->+f->(x) (18). Решением системы (18) будет вектор-функция y->=->(x), которая обращает
(17) в тождество:d->/dx=A(x) ->+f->(x) (19). Система (18) называется однородной, если f->=0, т.е.
когда она имеет вид: dy->/dx=A(x)y-> (20). И неоднородной, если f->0
Билет №48
Нормальная система линейных однородных уравнений с непрерывными коэффициентами. Теоремы: единственности, о тривиальном решении, о линейной комбинации и о линейной зависимости решений.
Линейные системы дифференциальных уравнений.
Линейной системой дифференциальных уравнение называется система уравнений вида:
dy1/dx=a11(x)y1+......+a1n(x)yn+f1(x); .......... ......... ;dyn/dx=an1(x)y1+......+ann(x)yn+fn(x) (17). Входящие в
(17) функции aik(x) и fi(x) предполагаются непрерывными на отрезке a,b. Это обеспечивает, как мы
видели ранее, выполнение условий теоремы существования и единственности решения в области
axb, -y1<,.......,-yn<. Таким образом, система (17) имеет единственное решение при любом
начальном условии (x0,y10,.....,yn0), где a<x0<b, -y10<........,-yn0<. Очень часто систему (17)
записывают в векторной форме. Если ввести матричную функцию:
И вектор – функции: , то систему (17) можно переписать как
dy->/dx=A(x)y->+f->(x) (18). Решением системы (18) будет вектор-функция y->=->(x), которая обращает
(17) в тождество:d->/dx=A(x) ->+f->(x) (19). Система (18) называется однородной, если f->=0, т.е.
когда она имеет вид: dy->/dx=A(x)y-> (20). И неоднородной, если f->0
Теорема 1: О тривиальном решении системы.
Если решение y->=->(x) однородной системы: d y->/dx=A(x )y-> (1), обращается в нуль в некоторой
точке х=х0, т.е. ->(x0)=0, то ->(x)0.
Доказательство: как видно из (1) , однородная система имеет тривиальное решение y->=0. Это
решение удовлетворяет нулевым начальным условиям при х0. Тогда в силу теоремы единственности
->(х) должно совпадать с тривиальным решением: ->(х) 0.
Теорема 2. Принцип суперпозиции. Пусть 1->(х),......., s->(х) – решения однородной системы (1).
Тогда их линейная
комбинация ->(x)=
![]() ckk->(х),
ck
так же является решением однородной
ckk->(х),
ck
так же является решением однородной
системы. Доказательство: проверим, что вектор-функция ->(x) является решением системы (1). Для
этого подставим выражение для ->(x) в (1) и учтем, что k->(х) – решения однородной системы. Тогда,
d->(x)/dx= ckdk->(х)/dx= ckA(x)k->(х)=A(x) ckk->(х)=A(x) ->. Определение. Если
имеются вектор-функции 1->(х),......., s->(х), то они называются линейно независимыми, если тождество
kk->(х)0 имеет место лишь при k=0, k=1,2,.......,s. В противном случае они называются
линейно зависимыми. Заметим, что если вектор-функции линейно зависимы, то постоянные векторы
1->(х0),......., s->(х0) будут также линейно зависимыми. Обратное неверно.
Теорема 3. О линейной зависимости решений однородной системы. Если постоянные векторы
1->(х0),......., s->(х0) линейно зависимы, то соответствующие им решения 1->(х),......., s->(х) однородной
системы (1) также линейно зависимы.
Доказательство: в силу зависимости постоянных векторов 1->(х0),......., s->(х0) существует ненулевая
система констант {i}, таких, что 11->(х0)+.......+ ss->(х0)=0. Построим вспомогательную
вектор-функцию ->(х)= 11->(х)+.......+ ss->(х), где k->(х) – решения системы (1), удовлетворяющие
начальным условиям: (х0, k->(х0)). По предыдущей теореме функция ->(х) так же является решением
однородной системы (1), причем ->(х0)=0. Тогда в соответствии с теоремой о тривиальном решении
->(х)0. Определение. Система n линейно независимых решений 1->(х),......., n->(х) однородной
системы (1), где n-порядок системы, называется фундаментальной системой решений.
Доказательство: выберем систему постоянных n-мерных векторов b->1,......,b->n, линейно независимых
между собой. Такие векторы всегда существуют: в качестве них, например, можно взять базис
n-мерного пространства. Определим вектор-функцию k->(х) как решение однородной системы (1),
удовлетворяющее начальному условию k->(х0)=bk->. В результате получим систему n решений:
1->(х),......., n->(х). По соответствующей теореме для линейной системы такие решения существуют и
являются единственными. Докажем их линейную независимость методом от «противного». Пусть
система 1->(х),......., n->(х) линейно зависима. Это означает, что существует ненулевой набор
констант 1,......,
n
таких, что![]() kk->(х)0,
но тогда
kk->(х)=
akbk->(х)=0,
kk->(х)0,
но тогда
kk->(х)=
akbk->(х)=0,
а это означает линейную зависимость системы постоянных векторов {b->1,....., b->n}, что невозможно
по построению.
Билет №49
Фундаментальная система решений. Теорема о ее существовании. Структура общего решения линейной однородной системы.
Теорема 5. Структура общего решения линейной однородной системы. Общее решение линейной
однородной системы (1) имеет вид:y->= ckk->(х) (2), где сk – некоторые константы, а
1->(х),......., n->(х) – фундаментальная система решений.
Доказательство: из теоремы о суперпозиции следует, что (2) является решением однородной
системы (1). Убедимся теперь в его общности , т.е. покажем, что любое решение (1), удовлетворяющее
заданным произвольным начальным условиям, может быть получено из (2) при соответствующем
выборе коэффициентов с1,......., сn. Пусть некоторое решение ->(х) системы (1) удовлетворяет
начальному условию ->(х0)=b->. В силу фундаментальности системы решений 1->(х),......., n->(х)
постоянные векторы 1->(х0),......., n->(х0) являются линейно независимыми и образуют базис n-мерного
пространства. Тогда любой вектор, в частности b->, можно разложить по этому базису:
b->= c11->(х0)+.......+ cnn->(х0), (3). Тогда вектор функция: y->(х)= ckk->(х) будет являться
решением системы (1), удовлетворяющим заданному начальному условию y->(х0)=b-> (см.(3)),а,
следовательно, по теореме единственности совпадает с ->(х).
Билет №50
Теоремы о максимальном числе линейно независимых решений, о линейном невырожденном преобразовании фундаментальной системы решений.
Теорема 6. О числе линейно независимых решений однородной системы. Максимальное число
линейно независимых решений однородной системы: dy->/dx=A(x )y-> (1) равно порядку системы.
Доказательство: «от противного». Допустим, что имеются (n+1) линейно независимых решений
однородной системы (1): 1->(х),......., n->(х), n+1->(х). Согласно доказанной теореме о структуре
общего решения системы (1) любое ее решение выражается формулой y->= ckk->(х) (2). В
частности, всегда
можно подобрать постоянные
![]() 1,...........,
n
таким образом, чтобы решение
1,...........,
n
таким образом, чтобы решение
n+1->(х) было представлено в форме: n+1->(х)= 11->(х)+........+ nn->(х). Запись данного
равенства в виде: 11->(х)+........+ nn->(х)- n+1->(х)=0 указывает на линейную зависимость
функций 1->(х),......., n->(х), n+1->(х), что противоречит первоначальному предположению.
Следовательно, число линейно независимых решений однородной системы (1) не превосходит ее
порядка n. Вывод. Совокупность решений линейной однородной системы образует линейное n-мерное
векторное пространство. Определение. Пусть задана система вектор-функций ->1(x),....., ->n(x) где:
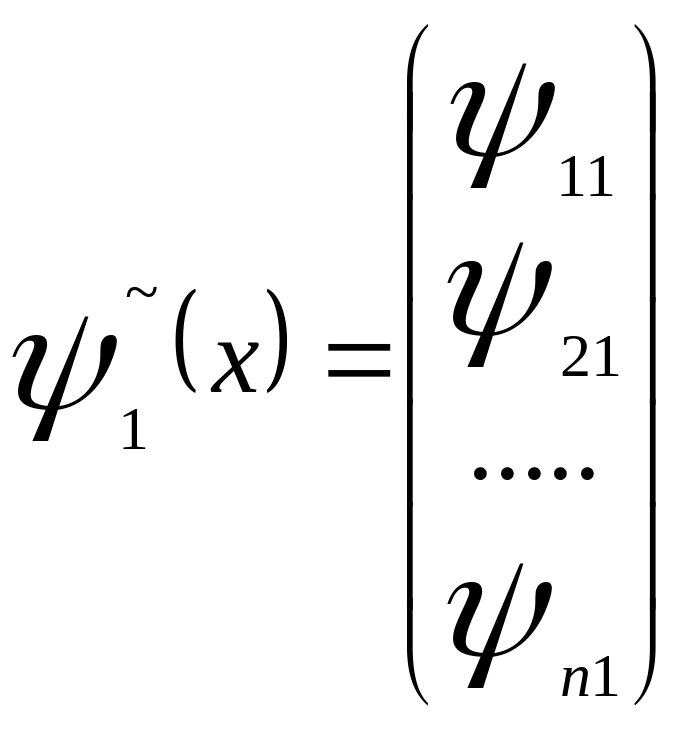 ,……………,
,……………,
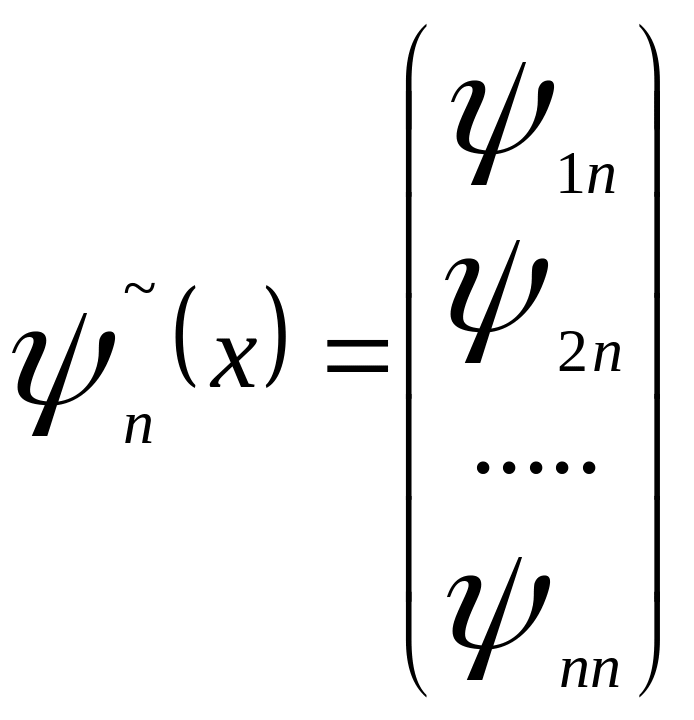 Определителем Вронского такой системы
называют
Определителем Вронского такой системы
называют
определитель размера n x n
W(x)=
->1(x),.....,
->n(x)
=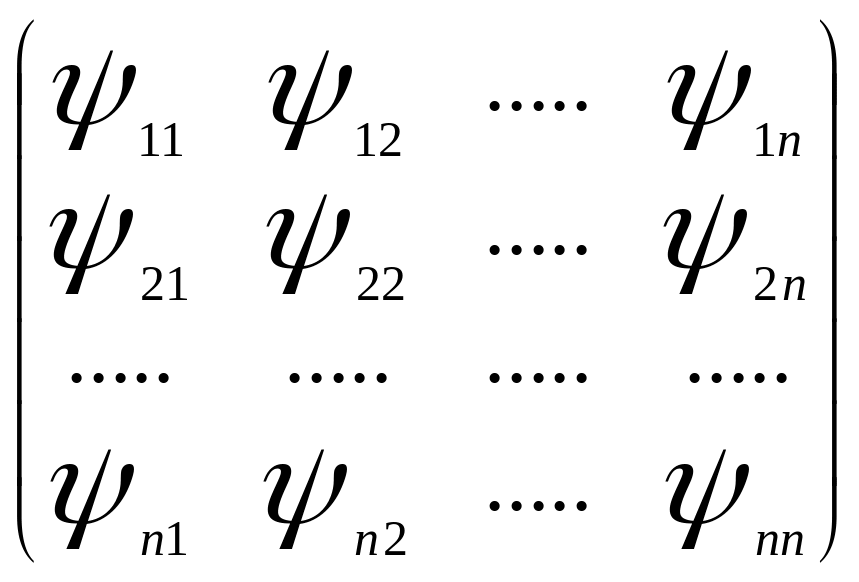 (4).
(4).
Теорема 9. О линейном преобразовании фундаментальной системы решений.
Если фундаментальную систему решений подвергнуть линейному невырожденному преобразованию,
то полученная система решений будет так же фундаментальной.
Доказательство: Допустим, что 1->(х),......., n->(х) – фундаментальная система решений линейной
однородной системы (1). Построим новую систему функций: ->j(x)= ajkk->(х), j = 1, 2,...,n (7),
где определитель матрицы А={ajk} отличен от нуля: detA 0. Совершенно ясно, что суперпозиция (7)
решений линейной однородной системы (1) сама является решением этой системы (см. теорему 2).
С другой стороны, соотношение (7) можно переписать в матричной форме: (->1(x) ->2(x) ...
..... ->n(x)) = (1->(х) ....... n->(х))AT (8). Из формулы (8) вытекает следующее равенство для
определителей ->1(x) ->2(x) ........ ->n(x)= 1->(х) ....... n->(х)detAT или W(x)=det AW(x),
W(x) и W(x) – определители Вронского для системы решений ->1(x),....., ->n(x) и 1->(х),......., n->(х)
соответственно. Поскольку исходная система решений фундаментальна, то W(x)0 ни при каких х. В
силу невырожденности преобразования: det A 0 и, следовательно, W(x) также отличен от нуля:
W(x)0. Это означает, что построенная система решений ->1(x),....., ->n(x) остается фундаментальной.
Билет №51
Определитель Вронского для системы решений нормальной системы линейных однородных уравнений, его свойства.
Теорема 7. Об определителе Вронского для системы линейно зависимых функций.
Для линейно зависимых вектор-функций ->1(x),....., ->n(x) определитель Вронского тождественно
равен нулю. Доказательство: пусть ->1(x),....., ->n(x) – линейно зависимые вектор функции, т.е.
существует ненулевой набор действительных постоянных 1,......, n (12+.........+n20) таких, что:
1->1(x)+.......+ n->n(x)0 (5). Соотношение (5) означает, что между столбцами определителя
Вронского (4) существует линейная зависимость. Следовательно, по свойствам определителей W(x)0.
Теорема 8. Об определителе Вронского для решений линейной однородной системы. Пусть при
некотором значении х=х0 определитель Вронского для решений линейной однородной системы (1)
обращается в нуль W(x0)=0 (6). Тогда для х W(x)0.
Доказательство: равенство (6) означает, что столбцы определителя W(x0) линейно зависимы, т.е.
линейно зависимы постоянные векторы 1->(х0),......., n->(х0). Если их принять за начальные условия,
то по теореме 3 линейно зависимыми будут и соответствующие решения системы (1) 1->(х),......., n->(х).
Следовательно, по ранее доказанной теореме 7 определитель Вронского тождественно равен нулю при
любых х. Следствие. Если определитель Вронского для решений линейной однородной системы не
обращается в нуль хотя бы в одной точке х0, то он ни при каких х не обращается в нуль, и эта система
решений линейно независима, т.е. фундаментальна.
Билет №52
Построение линейной однородной нормальной системы дифференциальных уравнений по ее фундаментальной системе решений.
Задача. Задана система n линейно независимых вектор-функций:. Требуется построить линейную
однородную систему дифференциальных уравнений, для которой вектор-функции и 1->(х),......., n->(х)
являются фундаментальной системой решений. Решение. Составим n определителей (n+1)-го порядка
для n неизвестныхфункций у1(х),......, уn(х) и положим их равным нулю
yk/ k1/ k2/ ...... kn/
y1/ 11/ 12/ ...... 1n/
y2/ 21/ 22/ ...... 2n/ = 0 ; k=1, 2,.........,n. (9)
...... ...... ........ ...... ...... ....
yn/ n1/ n2/ ...... nn/
Каждое из построенных уравнений (9) является линейным дифференциальным уравнением первого
порядка, разрешенным относительно производной. В самом деле, если разложить определитель по
первому столбцу, то перед производной yk/(х) появится определитель Вронского W(x), который для
системы линейно независимых функций 1->(х),......., n->(х) отличен от нуля для всех х, и на него можно
поделить обе части уравнения. В результате придем к: dyk/dx=(1/W(x))bk1(x)y1+ bk2(x)y2+....
.....+ bkn(x)yn; k=1,2,......,n (10). Уравнения (10) представляют собой однородную нормальную
систему линейных дифференциальных уравнений первого порядка. Теперь легко проверить, что
функции 1->(х),......., n->(х) являются решениями системы (10). Например, при подстановке
yk=k1->
(k=![]() )
в (9) получаем два одинаковых столбца
(первый и второй) определителя, и (9)
)
в (9) получаем два одинаковых столбца
(первый и второй) определителя, и (9)
переходит в тождество. Таким образом, система линейно независимых функций 1->(х),......., n->(х)
является фундаментальной системой решений построенной линейной однородной системы (9).
Билет №53
Формула Лиувилля для определителя Вронского решений нормальной системы.
Вычислим производную определителя Вронского, составляемого для фундаментальной системы
решений 1->(х),......., n->(х) линейной однородной системы: dy->/dx=A(x)y-> (1). В соответствии с
ранее установленным
правилом: (d/dx)W(x)=![]() Wk(x),
(2), где
Wk(x),
(2), где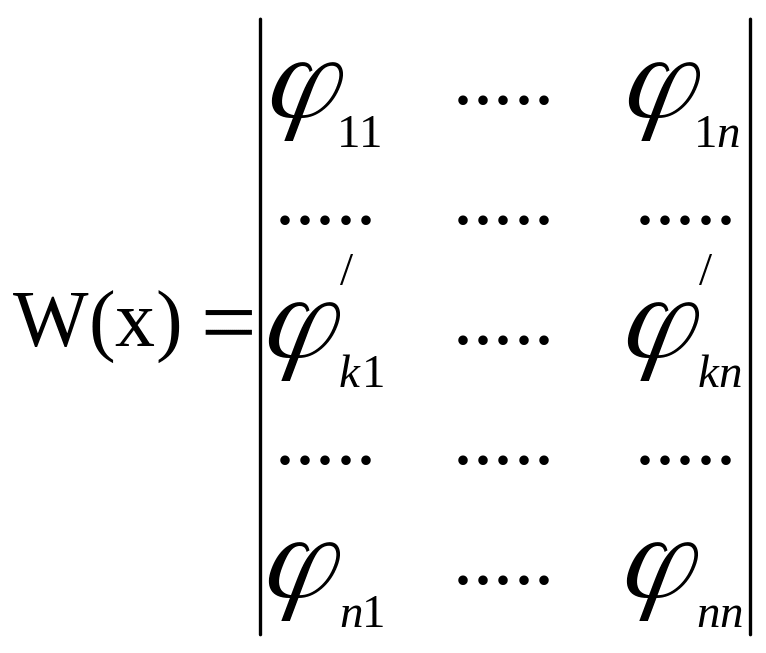 (3)
(3)
Поскольку вектор-функции 1->(х),......., n->(х) являются решениями однородной системы (1),
справедлива система
тождеств: dkm/dx=![]() akjjm,
m=1,2,...........,n.
Подставляя эти равенства в (3),
akjjm,
m=1,2,...........,n.
Подставляя эти равенства в (3),
имеем: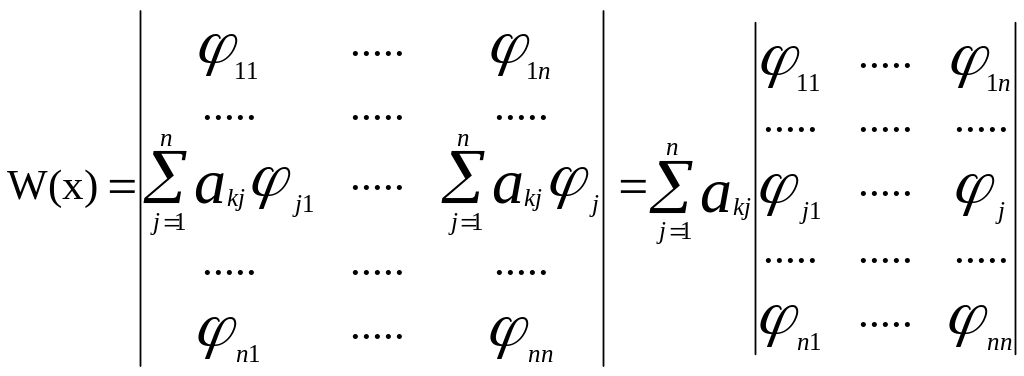
У определителей в правой части при jk есть совпадающие строки, поэтому отличным от нуля будет
лишь определитель с j=k, который является определителем Вронского. Поэтому:
Wk(x)= akjW(x)jk=akkW(x), и согласно (2): dW(x)/dx=W(x) akk=W(x)Spur A (4). Здесь
ведено традиционное обозначение суммы диагональных элементов матрицы: Spur A = akk,
называемое ее следом. В частности, для единичной матрицы Е размера (n x n) Spur E=n.
Решая дифференциальное уравнение первого порядка (4) для W(x), находим:
W(x)=W(x0)exp![]() Spur
A(t)dt.
(5). Формула
(5) и есть искомая формула Лиувилля.
Spur
A(t)dt.
(5). Формула
(5) и есть искомая формула Лиувилля.
Билет №54
Теорема об общем виде решения линейной неоднородной системы дифференциальных уравнений.
