2. Полный факторный эксперимент

Эксперимент, в результате которого все независимые переменные варьируются на всех выбранных уровнях, называется полным факторным экспериментом (ПФЭ). Количество опытов при ПФЭ подсчитывается так: N = kⁿ, где k — количество уровней, n — число факторов.

Ввиду того, что факторы различны по физической природе и изменяются в различных динамических диапазонах, для дальнейшей формализации процесса анализа и независимости полученных результатов от изменения масштаба входных величин факторы предварительно кодируют. Для этой цели используют соотношение

(2.1)

где — граничные значения варьирования независимыми переменными, которые или заданы или выбираются экспериментатором самостоятельно на основании априорной информации об объекте.

Таким образом, операция кодирования независимых переменных заключается в переносе центра координат в точку , называемую в дальнейшем центром плана эксперимента.

В кодированной системе на основании выражения (2.1) будут соблюдаться соответствия:

.

В дальнейшем будут использоваться кодированные переменные.

Построенная таким образом матрица обладает рядом ценных свойств:

1) ортогональности, которое обеспечивает независимость оценок коэффициентов модели

где — номера вектор-столбцов соответствующих факторов; i — текущая точка факторного пространства, в которой производится эксперимент; иными словами, данное свойство можно сформулировать так: скалярное произведение вектор-столбцов матрицы планирования равно нулю;

2) симметричности, которое обеспечивает независимость свободного члена

т. е. сумма элементов вектор-столбцов равна нулю, точки, в которых проводятся опыты, расположены симметрично по отношению к центру плана;

3) нормировки, обеспечивающее одинаковую дисперсию оценки коэффициентов,

Последнее равенство вытекает из того, что кодированные факторы принимают только значение ±1.

Расчет и статистическая оценка коэффициентов уравнения регрессии, полученного на основании плана ПФЭ, основаны как и при пассивном эксперименте, на применении регрессионного анализа. Ввиду того что матрица плана обладает свойством ортогональности, все расчеты чрезвычайно упрощаются. Это обусловлено тем, что кова­риационная матрица С^─1 в выражении для определения оценок коэффициентов

оказывается диагональной, что приводит к системе независимых оценок коэффициентов уравнения регрессии

; (2.2)

Каждый коэффициент рассчитывается независимо от других, причем общее число коэффициентов не должно превышать числа уравнений, из которых они определялись, а это число совпадает с числом строк матрицы планирования, определяемого соотношением N == 2ⁿ.

В соответствии со свойством нормировки матрицы плана полного факторного эксперимента выражение для определения оценки коэффициента уравнения регрессии при двухуровневом эксперименте окончательно запишется в виде

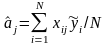(2.3)

где — «среднее построчное» значение выходной величины объекта в i-й строке матрицы плана.

Для определения оценки коэффициента необходимо матрицу плана дополнить вектор-столбцом фиктивной переменной , тождественно равной единице, как это пока­зано в табл. 2.2.

Ввиду того, что вектор-столбцы матрицы плана обладают условием симметричности, то

Следовательно, вектор-столбец фиктивной переменной будет ортогональным вектор-столбцам независимых переменных, и поэтому оценка свободного члена будет определяться независимо от оценок в соответствии с выражением (2.3):

Если модель содержит линейные парные взаимодействия факторов , то для определения оценок коэффициентов при них матрица плана дополняется вектор-столбцом для взаимодействия. Причем чередование знаков, в вектор-столбце получают путем перемножения знаков входящих в него вектор-столбцов и . В табл. 2.2 данная процедура проведена для определения оценки коэффициента при взаимодействии . Полученный таким образом вектор-столбец будет обладать тремя перечисленными выше свойствами матрицы планирования — ортогональности, симметричности и нормировки. Следовательно, оценка коэффициента при линейном взаимодействии находится независимо на основании того же выражения (2.3):

Найденные таким образом оценки коэффициентов мо­дели показывают степень влияния факторов и их взаимодействия на выходную величину. Если перед коэффициентом стоит знак плюс, то с увеличением данного фактора выходная величина увеличивается, а если стоит знак минус, то наоборот.

Регрессионный анализ исходит из предпосылки о случайности погрешностей, которые накладываются на входные и выходные величины. Однако, если проводить опыты в том порядке, в каком следуют строки матрицы планирования, построенной в соответствии с правилом (тем более для случая проведения серии параллельных опытов в каждой точке факторного пространства), то чем больший порядковый номер фактора, тем при большем числе опытов его уровень не изменяется. Для самого «старшего» фактора п его уровень остается неизменным (зафиксированным) в течение N/2 опытов. При этом реализация случайной погрешности задания факторов будет зафиксирована и становится систематической.

Таким образом, в течение большого числа опытов фактор, например х_n, будет задан с систематической погрешностью, что приведет к смещению оценок коэффициентов. Известно, что случайность величины проявляется во множестве ее выборок. Поэтому, чтобы оставить только случайную погрешность в установке уровней факторов с нулевым математическим ожиданием, все опыты осуществляют в случайном порядке — производят рандомизацию эксперимента. Рандомизация заключается в проведении опытов в случайном порядке. В заключение следует заметить, что возможны случаи, когда рандомизацию осуществить нельзя. Это бывает в тех случаях, когда последовательность условий проведения опытов является определенным параметром. Например, испытание катушки индуктивности с железным сердечником, когда форма петли гистерезиса зависит от предыдущей рабочей точки.