14. Метод вариации произвольных постоянных

Если правая часть не имеет специального вида, то используется метод Лангранджа (метод вариации произвольных постоянных)

Рассмотрим его. Пусть найдено y_o.o.=c₁(x)α(x)+c₂(x)β(x). Полагаем, что c₁=c₁(x) и c₂=c₂(x). То есть y=c₁(x)α(x)+c₂(x)β(x). Продифференцируем и подставим неоднородное уравнение и получим, что последние 2 слагаемых = f(x), то есть для нахождения c₁ и c₂ необходимо решить систему:

Если правая часть представляет собой сумму 2-х функций, то необходимо решать 2 неоднородных уравнения, и сумма 2-х частных решений будет частым решением исходного уравнения

15. Системы обыкновенных дифференциальных уравнений

- нормальная система

Если правые части представляют собой линейные функции, то система называется линейной. Если правые части не содержат в явном виде переменных t, то система называется однородной, в противном случае неоднородной

16. Числовые ряды. Основные теоремы о сходимости

Пусть дана последовательность чисел а₁,а₂,а₃,…,а_n-1,a_n.Сумма этой числовой последовательности называется числовым рядом.

Сумма конечного число членов ряда S₁=a₁, S₂=a₁+a₂, S₃=a₁+a₂+a₃ … называется частичными суммами, если существует конечный предел , то ряд называется сходящимся. Если последовательность частичных сумм не имеет предела, то ряд расходящийся и не имеет суммы.

Отбросим конечное число первых членов ряда и получим n-ый остаток ряда (r_n).

Теорема: для сходящегося ряда предел остатка равен 0

Теорема «Необходимый признак сходимости ряда»: общий член сходящегося ряда стремится к нулю . Если же предел не стремится к нулю, то ряд расходится

Теорема: если ряд сходится и сумма его равна S, то ряд (где с – некоторая постоянная) тоже сходится и сумма его равна cS.

Теорема: если сходятся ряды и , и суммы их равны соответственно S_a и S_b, то ряд тоже сходится, причем сумма его равна S_a+S_b

17. Положительные числовые ряды. Признак Коши и Деламбера.

Положительным называется ряд, члены которого неотрицательны, то есть a_n≥0

Для того, чтобы положительный ряд сходился, необходимо и достаточно, чтобы последовательность частичных сумм была ограничена сверху

Признак Деламбера: если члены последовательности ряда a_n таковы, что существует предел 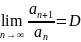, то при D<1 ряд сходится, при D>1 ряд расходится, при D=1 требуется дополнительное исследование.

Признак Коши: если члены ряда a_n таковы, что существует предел , то при К<1 ряд сходится, при K>1 ряд расходится, при K=1 требуется дополнительное исследование.

18. Знакочередующиеся числовые ряды. Абсолютная и условная сходимости.

Ряд вида a₁-a₂+a₃-a₄+…+(-1)ⁿ⁺¹a_n+… (1), где a_n≥0 называется знакочередующимся

Признак Лейбница: Если члены ряда таковы, что: 1)каждый следующий, меньше предыдущего; 2) , то ряд (1) сходится, причем сумма его последовательности меньше а₁

Рассмотрим ряды с членами произвольных знаков (1), с каждым рядом можно связать положительный ряд, состоящий из модулей членов данного ряда (2)

Если сходится ряд из модулей (2), то сходится ряд (1)

Ряд (1) называют абсолютно-сходящимся, если ряд (2) сходится.

Если ряд (1) сходится, а ряд (2) расходится, то ряд (1) называют условно-сходящимся