22.Исследование функции на выпуклость, вогнутость. Точки перегиба.

Рассмотрим на плоскости кривую y = f(x), являющуюся графиком однозначной дифференцируемой функции f(x).

Определение 1.

Кривая обращена выпуклостью вверх на интервале (а, b), если все точки кривой лежат ниже любой ее касательной на этом интервале.

Кривая обращена выпуклостью вниз на интервале (b, с), если все точки кривой лежат выше любой ее касательной на этом интервале.

Кривую, обращенной выпуклостью вверх, называют выпуклой, а обращенную выпуклостью вниз – вогнутой.

На рисунке показана кривая, выпуклая на интервале (a, b) и вогнутая на интервале (b, с). Направление выпуклости кривой является важной характеристикой ее формы.

Теорема 1.

Если во всех точках интервала (a, b) вторая производная функции отрицательна, т.е. f^//(x) < 0, то кривая y = f(x) на этом интервале обращена выпуклостью вверх (кривая выпукла).

Доказательство:

Возьмем в интервале (a, b) произвольную точку x = x₀ и проведем касательную к кривой в точке с абциссой х = х₀. Теорема будет доказана, если мы установим, что все точки кривой на интервале (a, b) лежат ниже этой касательно, т.е. ордината любой точки кривой y = f(x) меньше ординаты y касательной при одном и том же значении x.

Уравнение кривой имеет вид: y = f(x).

Уравнение же касательной к кривой в точке х = х₀ имеет вид:

у(вектор) – f(x₀) = f^/(x₀)(x-x₀) или y(вектор) = f(x₀) + f^/(x₀)(x-x₀).

Из уравнений следует, что разность ординат кривой и касательной при одном и том же значении x равна: y – y(вектор) = f(x) - f(x₀) - f^/(x₀)(x-x₀).

Применяя теорем Лагранжа к разности f(x) - f^/(x₀), получим

y – y(вектор) = f^/(с)(x-x₀) - f^/(x₀)(x - x₀) (где с лежим между x₀ и х)

или y – y(вектор) = [f^/(с) - f^/(x₀)](х - x₀)

К выражению, стоящему в скобках снова применяем теорему Лагранжа; тогда y – y(вектор) = f^//(с₁)(с - x₀) - (x - x₀) (где с₁ лежим между x₀ и с).

Рассмотрим сначала тот случай, когда x > x₀. В этом случае x₀ < c₁ < c < x; так как (x - x₀) > 0, с – х₀ > 0

И так как, кроме того, по условию f^//(c₁) < 0

То из равенства следует, что y – y(вектор) < 0.

Рассмотрим теперь случай, когда х < х₀. В этом случае х < c < c₁ < х₀ и х – х₀ < 0, с – х₀ < 0, а так как, по условию f^//(c₁) < 0, то из равенства следует, что y – y(вектор) < 0.

Таким образом, мы доказали, что любая точка кривой лежит ниже касательной к кривой, каковы бы ни были значения х и х₀ на интервале (a, b). А это значит, что кривая выпукла. Теорема доказана.

Определение 2.

Точка, определяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба кривой.

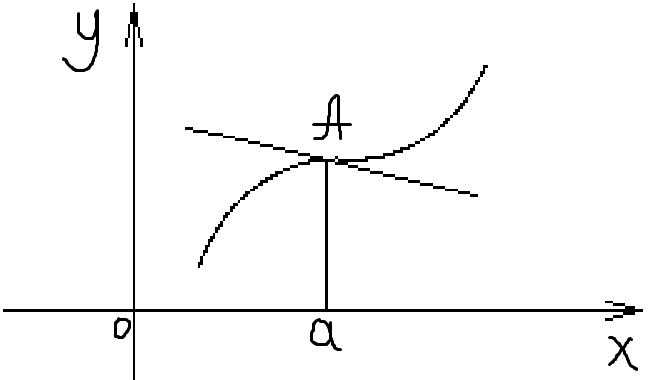
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, так как с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.

Теорема 2.

Пусть кривая определяется уравнением y = f(x). Если f^//(a) = 0 или f^//(a) не существует и при переходе через значение х = а производная f^//(х) меняет знак, то точка кривой с абсциссой х = а есть точка перегиба.

Доказательство.

1. Пусть f^//(х) < 0 при х < a и f^//(х) > 0 при х > a.

Тогда при x < a кривая обращена выпуклостью вверх и при x > a – выпуклостью вниз. Следовательно, точка А кривой с абсциссой х = а есть точка перегиба.

2. Если f^//(х) > 0 при х < b и f^//(х) > 0 при x > b, то x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Следовательно, точка B кривой с абсциссой х = b есть точка перегиба.