
- •Санкт-петербургский государственный Технологический институт (Технический университет)
- •Содержание Введение
- •1. И сходные физические, математические модели. Постановка задачи.
- •1.1 Нелинейная модель с распределенными параметрами (основная модель)
- •1.2 Нелинейная модель с сосредоточенными параметрами
- •1.3 Линейная модель с сосредоточенными параметрами
- •1.4 Исходные данные
- •2. Обработка экспериментальных данных. Построение оценочной функции регрессии α по u
- •3.Определение момента установления температуры окружающей среды
- •3.1 Отделение корней
- •3.2 Уточнение корня методом половинного деления
- •3.3 Решения уравнения комбинированным методом
- •3.4 Решение уравнений методом итераций
- •4. Вычисление интеграла I для линейной модели с сосредоточенными параметрами
- •4.1. Вычисление интеграла I по формуле прямоугольников
- •4.2. Вычисление интеграла по формулам трапеций
- •4.3. Вычисление интеграла по формуле парабол (методом Симпсона)
- •5. Приближенное решение задачи Коши (для нелинейной модели с сосредоточенными параметрами)
- •5.1. Решение задачи Коши методом Эйлера
- •5.2. Решение задачи Коши методом Рунге-Кутта
- •Заключение
- •Список используемой литературы
3.Определение момента установления температуры окружающей среды
Закон изменения температуры окружающей среды:

Где

Момент времени t0 находим, решая уравнение:


обозначим:

Тогда
уравнение приобретает вид:

Требуется
приближенно найти корень данного
уравнения, имеющий
 .
.
3.1 Отделение корней
Нахождение отрезка [a, b], содержащего наименьший положительный корень уравнения.
Достаточные условия единственности корня уравнения на [a, b]:
1)
2) строго монотонна на [a,
b],
то есть
строго монотонна на [a,
b],
то есть
 или
или
 на [a,
b].
на [a,
b].
В данном случае:




После некоторых преобразований найдем T:
T=2.03918
3.2 Уточнение корня методом половинного деления
Идея
метода состоит в нахождении приблизительного
значения корня уравнения
на
[a,
b]
путем последовательного приближения
к корню с концов отрезка. Положим a=a0,
b=b0
и будем делать на i-м
шаге один из концов полу суммой
 .
Соответственно, при стремлении числа
шагов к бесконечности, оба конца
сужающегося отрезка будут стремиться
к искомому корню. Условием же окончания
алгоритма в данном случае является:
.
Соответственно, при стремлении числа
шагов к бесконечности, оба конца
сужающегося отрезка будут стремиться
к искомому корню. Условием же окончания
алгоритма в данном случае является:

Откуда:

n |
an |
bn |
|
0 |
2.02 |
2.06 |
4*10-2 |
1 |
2.02 |
2.04 |
2*10-2 |
2 |
2.03 |
2.04 |
1*10-2 |
3 |
2.035 |
2.04 |
5*10-3 |
4 |
2.0375 |
2.04 |
2.5*10-3 |
5 |
2.03875 |
2.04 |
1.25*10-3 |
6 |
2.03875 |
2.03938 |
6.3*10-4 |
7 |
2.03906 |
2.03938 |
3.2*10-4 |
8 |
2.03906 |
2.03922 |
1.6*10-4 |
9 |
2.03914 |
2.03922 |
8*10-5 |

 .03918
.03918
3.3 Решения уравнения комбинированным методом
Уравнение комбинированного метода:
,
где

Пусть
[a,
b]
– промежуток локализации корня. Условие
применения комбинированного метода –
сохранение выпуклости графика f(t)
на [a,
b],
то есть
 (выпуклость вниз) или
(выпуклость вниз) или
 (выпуклость вверх) на [a,
b].
(выпуклость вверх) на [a,
b].
а)
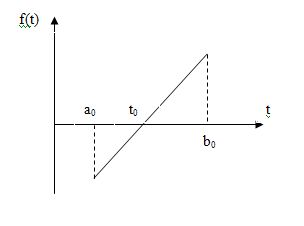
 >0,
>0,

в)
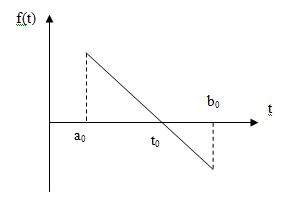
<0,
б)
>0,

г)
<0,
Если
 ,
то метод касательной применяется с
точки b:
,
то метод касательной применяется с
точки b:
 Слева
Слева
 Справа
Справа
Если , то метод касательной применяется с точки a и в расчетных формулах a меняется на b и наоборот.
Условие
окончания вычислений от:
 (
( ).
).
Подставив исходные данные, получим:

В нашем случае они положительны и больше нуля, что соответствует рисунку под буквой а).
После некоторых преобразований получим результаты расчетов, сведем их в таблицу:
n |
an |
bn |
|
0 |
2.02 |
2.06 |
0.04 |
1 |
2.03902 |
2.03927 |
2.50883*10-4 |
2 |
2.03915 |
2.03915 |
1.06801*10-8 |



t
t0
a0
b0
f(t)
ξ=2.03915
