9. Метод узловых потенциалов.

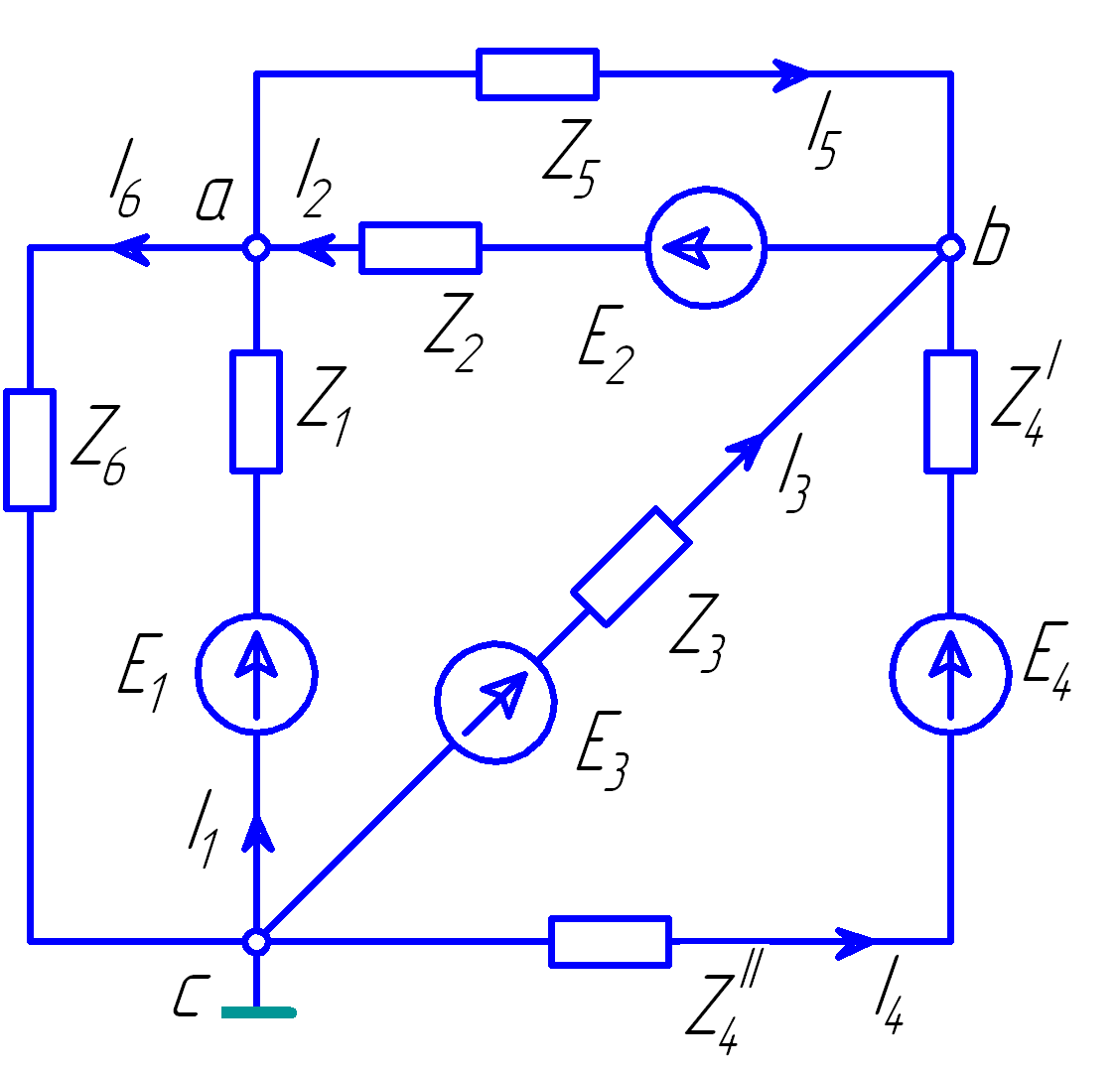
Рис. 4

Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно (m-1), где m – число узлов в схеме.

Пусть имеем схему по рис. 4, в которой примем потенциал точки С равный нулю φ_c = 0.

Допустим, что φ_a  и φ_b  известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС

(1)

Запишем уравнение по первому закону Кирхгофа для узла а:

(2),

и подставим значения входящих в него токов, определенных выше:

(3).

Сгруппировав соответствующие члены, получим:

(4).

Аналогично можно записать для узла b:

(5)

(6)

(7).

Совместное решение (4) и (7) относительно φ_a  и φ_b  позволит определить искомые потенциалы данных точек.

Система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами:

1.      В левой части i-го уравнения записывается со знаком «+» потенциал φ_i  i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей Y_ii  ветвей, присоединенных к данному i-му узлу, и со знаком «-» потенциал φ_k соседних узлов, каждый из которых умножен на сумму проводимостей Y_ik  ветвей, присоединенных к i-му и k-му узлам.

Из сказанного следует, что все члены φ_iY_ii, стоящие на главной диагонали в левой части системы уравнений, записываются со знаком «+», а все остальные - со знаком «-», причем Y_ik = Y_ki. Последнее равенство обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.

2.      В правой части i-го уравнения записывается так называемый узловой ток J_i, равный сумме произведений ЭДС ветвей, подходящих к  i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком «+», если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак «-». Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.

10. Баланс мощности.

Под балансом мощностей электрической цепи понимается равенство мощностей, развиваемой всеми источниками энергии данной цепи, и мощности, потребляемой всеми приемниками той же цепи (закон сохранения энергии).

Если на участке цепи ab имеется источник энергии с ЭДС и по этому участку протекает ток , то мощность, развиваемая этим источником, определяется произведением .

Каждый из множителей этого произведения может иметь положительный или отрицательный знак относительно направления ab. Произведение будет иметь положительный знак, если знаки расчетных величин и совпадают (мощность, развиваемая данным источником, отдается приемникам цепи). Произведение будет иметь отрицательный знак если знаки и противоположны (источник потребляет мощность, развиваемую другими источниками). Примером может служить аккумулятор, находящийся в режиме зарядки. В этом случае мощность данного источника (слагаемое ) входит в алгебраическую сумму мощностей, развиваемых всеми источниками цепи, с отрицательным знаком. Аналогично определяется величина и знак мощности, развиваемой источником тока. Если на участке цепи mn имеется идеальный источник тока с током , то мощность развиваемая этим источником, определяется произведением . Как и в источнике ЭДС знак произведения определяется знаками множителей.

Теперь можно записать общий вид уравнения баланса мощностей

.

Для цепи, представленной на рис. 5 уравнение баланса мощности имеет вид

.

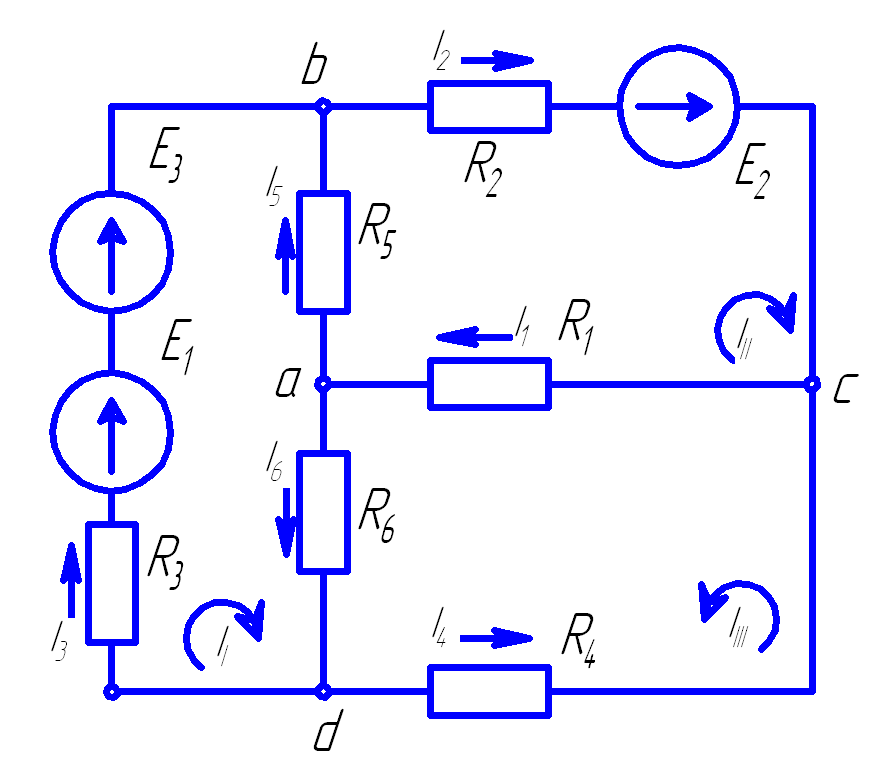
Рис. 5