
- •Интегральное исчисление Неопределенный интеграл. Первообразная, неопределенный интеграл, правила интегрирования.
- •Пример 1. Найти первообразные для функции , проходящие через точки м(2;4) и м(0;-4). Сделать рисунок.
- •Свойства неопределенных интегралов
- •Методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям, метод подстановки.
- •Простейшие преобразования
- •Интегрирование дробно-рациональных функций.
- •Интегрирование тригонометрических функций.
- •Интеграл вида .
- •Интеграл вида если функция r является нечетной относительно cosx
- •Интегрирование иррациональных функций. Тригонометрические подстановки.
- •Интеграл вида где n- натуральное число
- •Несколько примеров интегралов, не выражающихся через элементарные функции
- •О технике интегрирования
Интеграл вида где n- натуральное число
С помощью
подстановки
 функция рационализируется.
функция рационализируется.
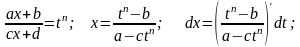
Тогда
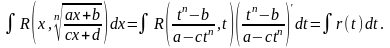
Пример 28.
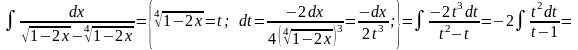
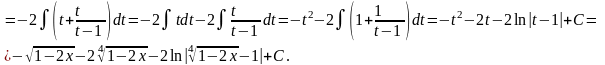
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.
Проиллюстрируем это на примере.
Пример 29.
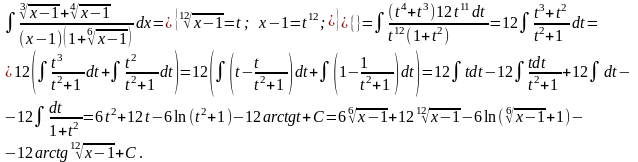
Тригонометрические подстановки
Теорема:
Интеграл вида
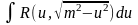 подстановкой
подстановкой
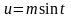 или
или
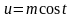 сводится к интегралу от рациональной
функции
сводится к интегралу от рациональной
функции
относительно sint или cost.
Пример30.
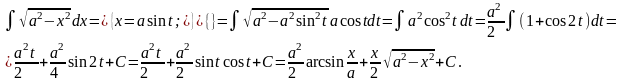
Теорема:
Интеграл вида
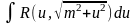 подстановкой
подстановкой
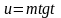 или
или сводится к интегралу от рациональной
функции относительно sint
и cost.
сводится к интегралу от рациональной
функции относительно sint
и cost.
Пример 31.
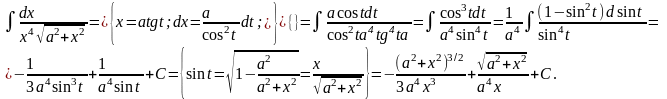
Теорема:
Интеграл вида
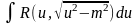 подстановкой
подстановкой
 или
или
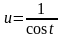
сводится к интегралу от рациональной функции относительно sint
или cost.
Пример 32.
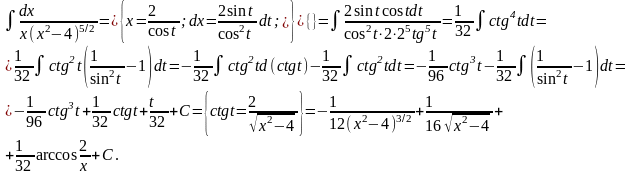
Интегралы вида
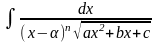
Интегралы вида,
где
 подстановкой
подстановкой
 приводятся к интегралу от иррационального
выражения.
приводятся к интегралу от иррационального
выражения.
Пример
33. Найти интеграл
 .
.
Решение.
 =
=
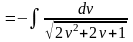 ,
мы получили интеграл вида
,
мы получили интеграл вида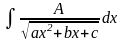 (II).
(II).
Несколько примеров интегралов, не выражающихся через элементарные функции
К таким
интегралам относится интеграл вида
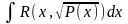 ,
где Р(х)- многочлен степени выше
второй. Эти интегралы называются
эллиптическими.
,
где Р(х)- многочлен степени выше
второй. Эти интегралы называются
эллиптическими.
Если степень многочлена Р(х) выше четвертой, то интеграл называется ультраэллиптическим.
Если все – таки интеграл такого вида выражается через элементарные функции, то он называется псевдоэллиптическим.
Не могут быть выражены через элементарные функции следующие интегралы:
 - интеграл Пуассона ( Симеон Дени Пуассон
– французский математик (1781-1840));
- интеграл Пуассона ( Симеон Дени Пуассон
– французский математик (1781-1840));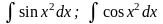 - интегралы Френеля (Жан Огюстен Френель
– французский ученый (1788-1827) - теория
волновой оптики и др.);
- интегралы Френеля (Жан Огюстен Френель
– французский ученый (1788-1827) - теория
волновой оптики и др.); - интегральный логарифм;
- интегральный логарифм;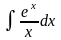 - приводится к интегральному логарифму;
- приводится к интегральному логарифму;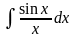 - интегральный синус;
- интегральный синус;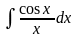 - интегральный косинус.
- интегральный косинус.
О технике интегрирования
Сравнительно редко удается дать конкретное правило интегрирования
функций, но и тогда когда оно есть, теоретическая схема не всегда является
рациональным путем. Интегрирование чаще всего может быть выполнено не
единственным способом. Выбор метода интегрирования обуславливается в основном наибольшим удобством, очевидностью применения того или иного метода, а также сложностью вычислений и преобразований. Владение операцией интегрирования заключается в умении произвести ее с минимумом затраченного времени и труда.
ПОМНИ! Изобретательность и навык приобретаются практикой при
решении достаточно большого числа примеров.
