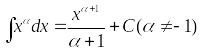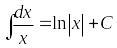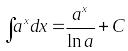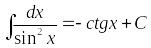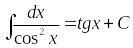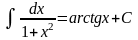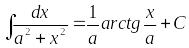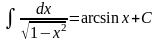Пример 1. Найти первообразные для функции , проходящие через точки м(2;4) и м(0;-4). Сделать рисунок.

Решение.

Множество всех первообразных функции есть 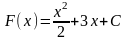, зная, что первообразная проходит через точку М(2;4), подставим ее координаты в предыдущее выражение и найдем С.

4=2+6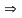+С С .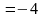

Искомой первообразной является функция 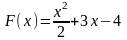, геометрически она собой представляет параболу .

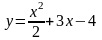Аналогично через точку М(0; 3) проходит парабола .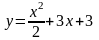

Графически это изображено на рисунке 2.

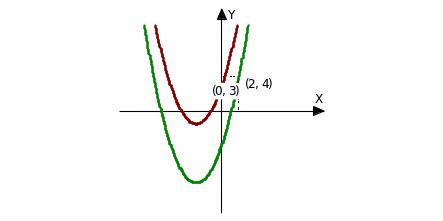
Рис. 2.

Совокупность всех первообразных для функции f(x), то есть выражение F(x) + C, где С – произвольная постоянная, называется неопределенным интегралом и обозначается

,

 

 

Теорема 3 (существование неопределенного интеграла)

Если функция непрерывна на данном множестве, то

существует первообразная, а значит, и интеграл .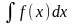

•  Знак 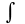называется знаком неопределенного интеграла;

• Функция f(x) называется подынтегральной;

• Произведение f(x)dx называется подынтегральным выражением;

• F(x) – одна из первообразных;

• х – переменная интегрирования;

• Процесс нахождения первообразной называется интегрированием.

 

! Помни: Правильность интегрирования всегда можно проверить

дифференцированием результата.

Пример 2. Найти неопределенные интегралы:

а) 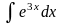; б) .

 

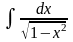Решение.

а) 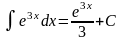, так как ;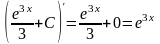

б) 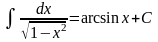, так как .

 

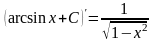1. Свойства неопределенных интегралов

Свойство 1. 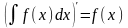, т. е. производная от неопределенного

интеграла равна подынтегральной функции.

Пример:

Свойство 2. 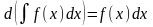, т. е. дифференциал от неопределенного

интеграла равен подынтегральному выражению.

Пример:

 

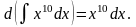
Свойство 3. .

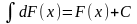Пример:

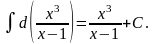
 Свойство 4. .

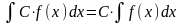Пример:

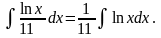
Свойство 5. (аддитивности) .

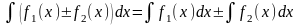Пример:

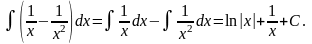
Свойство 6. (линейности) .

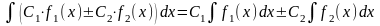Пример:

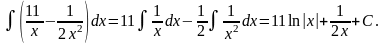
Свойство 7. Если , то .

Первые три свойства вытекают из определения неопределенного интеграла.

Для доказательства свойств 6 и 7 можно продифференцировать левые и правые части по х и использовать свойство 1 неопределенных интегралов и свойства производных.

 

Доказательство свойства 6.

.

 

 

 

.

 

Доказательство свойства 7.

.

.

 

 

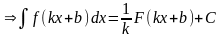Пример 3. Найти неопределенные интегралы:

 

а) б)

 

Решение. Используя свойства 5, 6 и 7, находим:

 

а)

 

б)

 

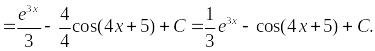
Таблица основных неопределенных интегралов

Используя таблицу базовых первообразных и на основании второго свойства неопределенного интеграла получим: если dF (x) = f (x)dx , то

∫ f (x)dx = F (x) + C .

Например, поскольку d (sin x) = cos xdx , то ∫cos xdx = sin x + C . Применяя аналогичное рассуждение к каждой из формул таблицы дифференциалов, получаем следующую таблицу простейших неопределенных интегралов, которая в высшей математике играет такую же роль, как таблица умножения в арифметике.

Таблица основных интегралов

№	Неопределенный интеграл	Частные случаи
1.	степенные функции	(при - формула 1 настоящей таблицы);
2.	логарифмические функции
3.	показательные функции
4.
5.
6.
7.	тригонометрические функции
8.
9.	обратно- тригонометрические функции
10.
11.

Замечание. В таблице основных интегралов предполагалось, что x

является независимой переменной. Однако формулы этой таблицы остаются

справедливыми и в случае, когда 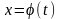, где 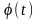– любая

дифференцируемая функция новой переменной t.

Теорема 4. (Об инвариантности формул интегрирования.)

Пусть – какая-либо известная формула

интегрирования и 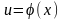– любая функция, имеющая непре-

рывную производную. Тогда .

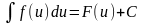Доказательство:

Из того, что следует , следует .

Возьмем теперь функцию F (u) = 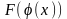; для ее дифференциала,

в силу теоремы об инвариантности вида первого дифференциала функции,

имеем 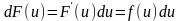отсюда

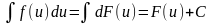
Итак, в силу доказанной теоремы, из справедливости формулы

∫ f (x)dx = F (x) + C, следует справедливость формулы ∫ f (u)du = F (u) + C ,

которая получается из первой формальной заменой x на u .

Таким образом, получаем обобщенную таблицу интегралов. Например,

будут справедливы формулы:

1. ;

2. ;

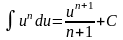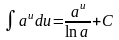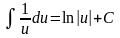3. и т.д.

Многие интегралы, предварительно преобразовав подынтегральное выражение, удается привести именно к такому табличному виду.

Так, например,

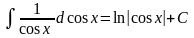- согласно третьей формулы.

Добавим в таблицу еще два интеграла.

.