
- •Интегральное исчисление Неопределенный интеграл. Первообразная, неопределенный интеграл, правила интегрирования.
- •Пример 1. Найти первообразные для функции , проходящие через точки м(2;4) и м(0;-4). Сделать рисунок.
- •Свойства неопределенных интегралов
- •Методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям, метод подстановки.
- •Простейшие преобразования
- •Интегрирование дробно-рациональных функций.
- •Интегрирование тригонометрических функций.
- •Интеграл вида .
- •Интеграл вида если функция r является нечетной относительно cosx
- •Интегрирование иррациональных функций. Тригонометрические подстановки.
- •Интеграл вида где n- натуральное число
- •Несколько примеров интегралов, не выражающихся через элементарные функции
- •О технике интегрирования
Простейшие преобразования
 ;
; ;
; .
.
Таблица дифференциалов
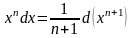 ;
7.
;
7.
 ;
; ;
8.
;
8.
 ;
; ;
9.
;
9.
 ;
; ;
10.
;
10.
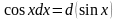 ;
; ;
11.
;
11.
 ;
; ;
12.
;
12.
 .
.
Пример
6. Найти интеграл
 .
.
Решение.
Внесем x под знак дифференциала
xdx = ,
прибавим 1 и
,
прибавим 1 и
умножим на (-1) под знаком дифференциала и перед интегралом, чтобы
выражение не изменилось. Тогда интеграл примет вид
 .
.
Метод 3. Интегрирование по частям
Способ интегрирования по частям основан на известной формуле производной произведения:
(uv) = uv + vu
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем:
 ,
а в соответствии с приведенными выше
свойствами неопределенного интеграла:
,
а в соответствии с приведенными выше
свойствами неопределенного интеграла:
 или
или
 .
(3)
.
(3)
Получили формулу (3) интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Формула (3) используется в тех
случаях, когда подынтегральное выражение
f (x)dx можно так представить
в виде udv , что стоящий в правой части
интеграл при надлежащем выборе выражение
u и dv может оказаться проще
исходного интеграла. Как правило,
подынтегральное выражение f(x)dx
представлено в виде произведения
различных по типу функций, например:
 ,
,
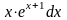 ,
,
 и т.д. При этом следует иметь ввиду, что
к u следует относить множители,
которые упрощаются при дифференцировании.
В соответствии с этим можно предложить
следующую вспомогательную таблицу:
и т.д. При этом следует иметь ввиду, что
к u следует относить множители,
которые упрощаются при дифференцировании.
В соответствии с этим можно предложить
следующую вспомогательную таблицу:
f (x)dx |
u |
dv |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 7.
Найти интеграл
 ,
применив интегрирование по частям.
,
применив интегрирование по частям.
Решение.

Таблицей можно воспользоваться и в случае если подынтегральная функция содержит либо логарифмическую, либо обратно - тригонометрическую.
Пример 8.
Найти интеграл
 ,
применив интегрирование по частям.
,
применив интегрирование по частям.
Решение.

! Формулу интегрирования по частям можно применять многократно, пока не упростятся подынтегральные функции, которые приведут к табличному интегралу.
Пример 9.
Найти интеграл
 ,
применив интегрирование по частям.
,
применив интегрирование по частям.
Решение.


 .
.
Как видно из примера 9 происходит неоднократное, последовательное применение формулы интегрирования по частям, что позволяет в итоге постепенно упростить функцию и привести интеграл к табличному.
Иногда после многократного, особенно после двукратного применения формулы интегрирования по частям, приходим в правой части к выражению, содержащему исходный интеграл, т.е. получаем уравнение с искомым интегралом в качестве неизвестного.
Такие интегралы называют циклическими.
Пример 10.
Найти интеграл
 .
.
Решение.


Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.


Таким образом, искомый интеграл найден путем преобразования исходной левой части равенства и полученной правой.
Пример 11.
Найти интеграл
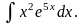 .
.
Решение.


Метод 4. Метод подстановки.
Если подынтегральная функция такова, что трудно выделить производ-
ную от какого либо промежуточного аргумента или его просто нет, то в этом
случае переменную интегрирования лучше заменить некоторой другой
функцией,
полагая
 ,
дифференцируя, получаем
,
дифференцируя, получаем
 ,
(предполагается, что
,
(предполагается, что
 и
и
 непрерывны). Тогда
непрерывны). Тогда
 ,
,
где
 новая
функция от аргумента
новая
функция от аргумента
 .
.
Если последний интеграл в результате такой замены свелся к таблич-
ному
и равен
 + C, то заданный интеграл определяют
путем возвращения к переменной х,
т.е. из уравнения
надо
найти обратную функцию
+ C, то заданный интеграл определяют
путем возвращения к переменной х,
т.е. из уравнения
надо
найти обратную функцию ,
и заменить
на φ(х).
,
и заменить
на φ(х).
С помощью подстановок такого рода удается избавится от корня, упро-
стить подынтегральную функцию и свести интеграл к табличному. Однако,
общего рецепта для выбора функции нет. В каждом конкретном случае
её подбирают индивидуально по виду подынтегрального выражения.
Пример12.
Найти интеграл
 .
.
Решение.

 .
.
Все дальнейшее изложение темы «Неопределенный интеграл» будет состоять в основном из рассмотрения различных подстановок.
Интегрирование выражений, содержащих квадратный трехчлен.
Следовательно, интегралы типа (I) и (II) преобразованием знаменателя сводятся к основным табличным интегралам № 8-11.
Пример 13.
Найти неопределенный интеграл

Решение.
 , применяя табличный интеграл
получаем
, применяя табличный интеграл
получаем

Для интегралов типа (III) и (IV), предварительно введем два вспомогательных интеграла, которые были получены одним из методов интегрированияметодом замены переменной:
 (3),
(3),
 (4),
(4),
где
,
в нашем случае, квадратный трехчлен
 .
.
Для нахождения данных интегралов необходимо в числителе, путем алгебраических выражений выделить производную квадратного трехчлена, стоящего в знаменателе, и представить в виде суммы двух интегралов сводимых к табличным.
Пример14.
Найти неопределенный интеграл

Решение.
Данный
интеграл разбиваем на сумму двух, затем
в первом числителе получаем производную
знаменателя :
:


Первый интеграл находим по вспомогательной формуле (3), второй интеграл сводится к интегралу типа (I):
 ,
,

 .
.

 ,
,
 ,
, ,
,
 ,
,
 ,
,
 ,
,
 -
где
-
где многочлен любой степени
многочлен любой степени
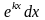


 ,
, ,
, ,
,
 ,
, ,
, ,
,