Метод опорных векторов в задаче регрессии.
Дана
совокупность данных: 
Требуется
построить функцию
,
которая наилучшим образом соответствует
этим данным.
Образуем
матрицу
составленную
из векторов выборки и пополненную
столбцом из единиц.
Вектор
коэффициентов обозначим
.
Неизвестные
регрессионные коэффициенты формально
представляют «решение» системы уравнений
Поскольку система обычно несовместна, то в качестве решения берется значение, доставляющее минимум функции:
(4.5’.1)
.
В
точке минимума
что
дает два условия (из которых каждое
есть следствие другого):
Как следствие получается правило определения вектора b.
При
условии, когда матрица
не имеет обратной или является плохо
обусловленной (что, как правило, есть
следствие зависимости столбцов исходных
данных), применяется так называемая
регуляризация. В(4.5.1) добавляется
слагаемое, предназначенное ограничивать
величину b.
(4.5’.2)
Тогда для вычисления получается формула
,
где Е-
единичная матрица.
Первое слагаемое в формуле (4.5’.2) можно расценить как штраф за не правильное предсказание - причем видом штрафной функция можно теперь распорядиться ( в формуле она взята квадратической ) . Если взять функцию штрафа в виде:
-линейный
штраф с амнистией внутри интервала
,
то получим задачу
Форма задачи напоминает об аналогичной задаче SVM. Рассмотрим SVM- регрессию сначала в линейном варианте, а затем и в нелинейном. Преимущество метода SVM-регрессии состоит в том, что не требуется знать конкретный вид нелинейной функции регрессии.
Уточним
постановку задачи SVM –регрессии. Для
каждой тоски выборки
установим
интервал
,
свободный от штрафования за неправильный
ответ. Вне интервала в пределах
определяемых переменными параметрами
устанавливается штраф.
Введение
послаблений
обеспечивает
выполнение условий:
(4.5’.3)
Вспоминаем,
что
- ширина полосы охватывающей плоскость
(линию) регрессии. Стремление увеличить
полосу означает стремление охватить
(замести) «опереться» на возможно
большее количество точек выборки. Эти
наводящие рассуждения приводят нас к
следующей модели.
Найти минимум функции
При условиях
(4.5’.4)
(4.5’.5)
,
Рис. 4.5’.1 Штрафная функция в задаче регрессии
В пределах интервала (-ε;ε) штраф за отклонение равен нулю. За пределами этого интервала нечувствительности штраф – линейная функция. Если штрафная функция – парабола, то задача эквивалентна методу наименьших квадратов.
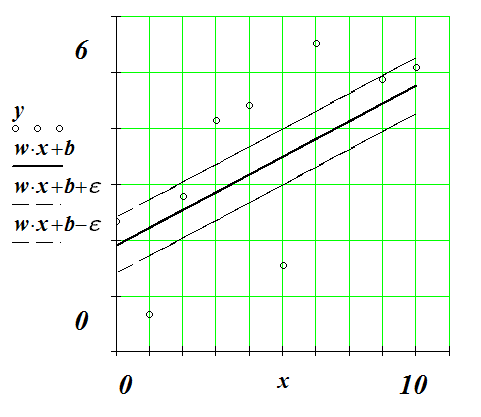
Рис. 4.5’.2 Полоска нечувствительности.
Образуем
функцию Лагранжа для нашей оптимизационной
задачи, введя множители Лагранжа
чтобы учесть, что отклонения
неотрицательны, и множители
для того чтобы учесть неравенства
(4.5’.4), (4.5’.5).
Функция Лагранжа получает вид:
(4.5’.6)
Продифференцируем
по w,b,
,
чтобы получить необходимые условия
минимума:
(4.5’.7)
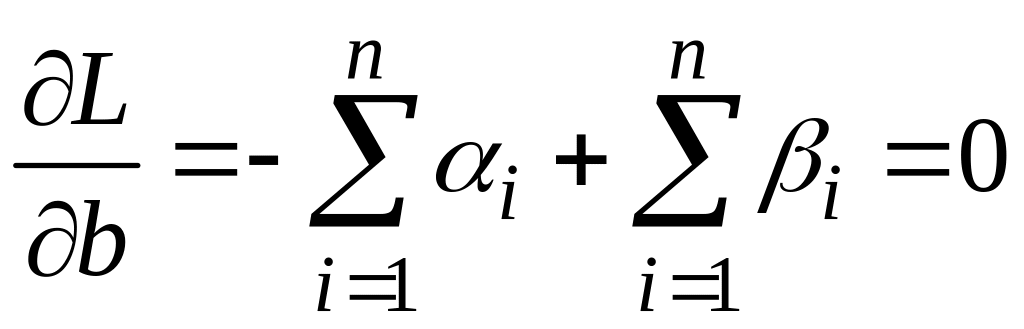(4.5’.8)
(4.5’.9)
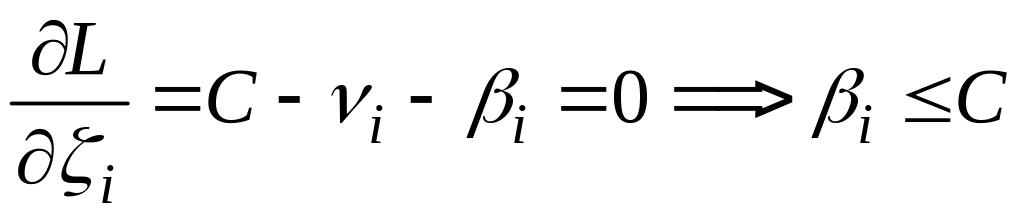(4.5’.10)
Полученные необходимые условия подставляем в функцию Лагранжа и получаем так называемую дуальную форму лагранжиана:
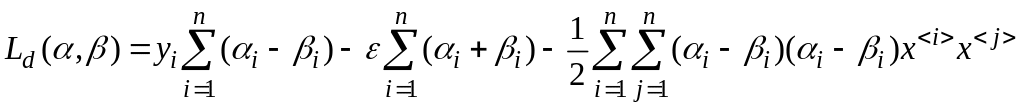(4.5’.11)
Теперь решается задача
при
условиях
и
.
После определения и , используя (4.5’.7) находим значение
,
которое определяет ширину полосы.
Опорные вектора лежат на границе полосы,
то есть это те точки, для которых
отклонения
равны нулю. Для этих переменных условия
дополняющей нежесткости, фигурирующие
в теореме Куна-Такера, приводят к тому,
что
Поэтому,
для опорных векторов
и
Для произвольного опорного вектора
если
(4.5’.12)
или, если
Практически вычисление b выполняется усреднением по опорным векторам.
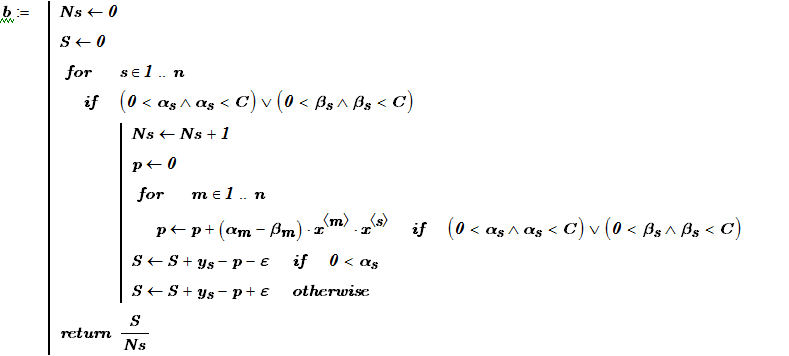
В итоге получено уравнение регрессии
(4.5’.13)
Особое преимущество метода SVM для решения задач восстановления зависимостей составляет его применения для нелинейных зависимостей. Аналогично тому, как это было для задач классификации, используем соответствующую «ядерную» функции(kernel function).
Корифеи метода SVM предлагают варианты:
(4.5’.14)
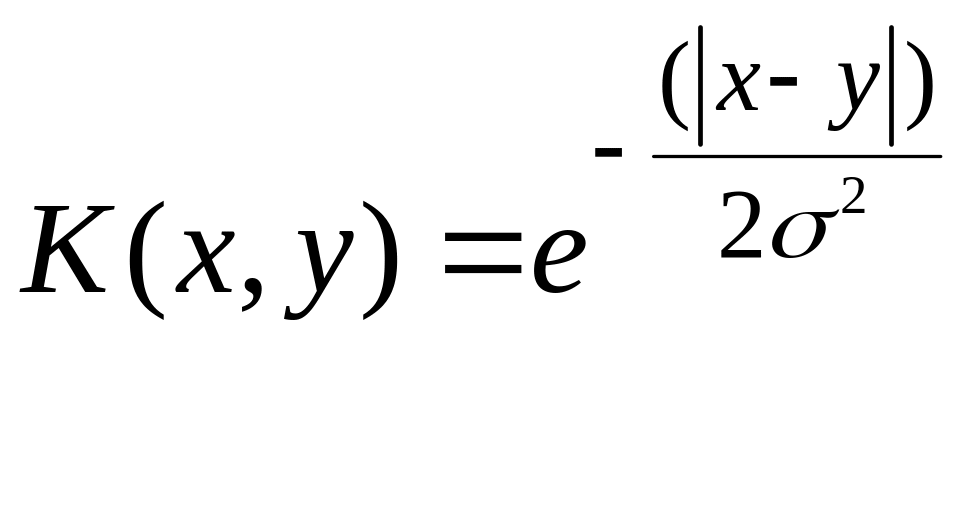(4.5’.15)
(4.5’.16)
Последний вариант сводит задачу к линейному случаю. В ядерном случае дуальный лагранжиан получает вид:
Формулы для смещения в пространстве отображения
(4.5’.17)
если или, если
Уравнение регрессии можно записать, не используя явного вида для вектора w:
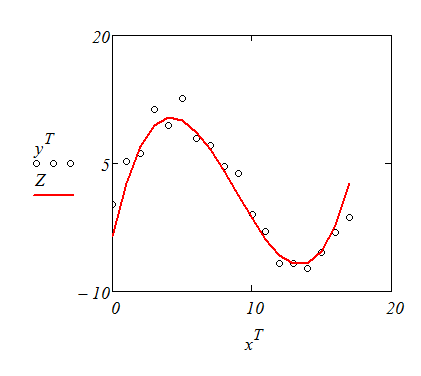
Рис. 4.5’.3 Результат, полученный с помощью функции ядра (4.5’.14) при d=3.
2. Расчет средней длины очереди в СМО открытого типа
Время поступления заявок в систему является случайной величиной. В инструментальных средах «имитационного» моделирования (в том числе и в среде Extendsim 7 Demo) реализованы возможности задавать различные законы распределения этой случайной величины. В данной работе предполагается, что поток заявок является простейшим потоком. Время, которое тратится на обслуживание одной заявки, также предполагается случайной величиной. Моменты завершения обслуживания можно считать потоком событий. За ним закрепилось название - поток обслуживания. В данной работе мы предполагаем, что это простейший поток. Интенсивности потоков заявок и потока обслуживания каналом будем обозначать соответственно λ и μ.
В некоторых инструментальных средах для имитационного моделирования задаются не параметры распределения, а средние времена
и
(3.2.1)
Te – среднее время между заявками (entities);
Ts - среднее время обслуживания (service) одним устройством (каналом) одной заявки.
Пусть имеется задача.
Автозаправочная станция имеет две заправочные стойки(n=2). Территория вокруг станции допускает пребывание в очереди на заправку не более m=3 машин. Машины на заправку прибывают с интенсивностью 2 машины в минуту. На заправку в среднем уходит 2 минуты.
В данной задаче заявка – это автомобиль. Канал обслуживания – это заправочная стойка.
Определим основные характеристики системы обслуживания, среди которых:
-вероятность
отказа заявки в обслуживании
;
-вероятность
выполнения обслуживания
;
-среднее число заявок A , обслуживаемых в единицу времени;
-среднее число занятых каналов обслуживания No;
-среднее число заявок в очереди (средняя длина очереди Lq);
-среднее
время ожидания заявки в очереди
;
-среднее время, которое заявка находится в системе Ts (ожидание + время обслуживания); Система может находиться в следующих состояниях:
– все
каналы свободны & очередь пуста;
– 1
канал занят обслуживанием & очередь
пуста;
……..
– k
каналов заняты обслуживанием &
очередь пуста ( k
< n
);
……..
– n
каналов заняты обслуживанием & очередь
пуста;
– n
каналов заняты обслуживанием & в
очереди 1 заявка;
……..
– n
каналов заняты обслуживанием & в
очереди j
заявок; (j
< m)
……..
– n
каналов заняты обслуживанием & в
очереди m
заявка.
Указанные
в перечне состояния имеют вероятности
,
определить которые и составляет задачу
моделирования системы массового
обслуживания. Составим уравнения для
вероятностей возможных состояний
системы.
Если система находится в состоянии – , оставаться в этом состоянии она может, если в течение ближайшего времени (Δt) не поступит новая заявка. Вероятность поступления заявки равна λΔt с точностью до бесконечно-малых по сравнению с Δt.
Если система находится в состоянии – , то перейти в состояние - она может, если в течение ближайшего времени (Δt) занятый канал освободится, вероятность чего равна μΔt с точностью до бесконечно-малых по сравнению с Δt.
Для
того, чтобы система перешла за время
Δt
в состояние-0 из других состояний (
например, из состояния –
)
необходимо, чтобы произошло освобождение
сразу двух каналов, вероятность этого
как произведение двух б.м. величин
является б.м более высокого порядка.
Поэтому дальше мы рассматриваем переходы
только между соседними состояниями.
В результате можно записать, что вероятность системы очутиться в момент времени t + Δt
в состоянии- , выражается равенством:
(3.2.2)
Легко видеть, что формула выражает вероятность суммы независимых событий, каждое из которых есть произведение вероятности на соответствующую условную вероятность.
Для
событий от
до
(
)
получим следующую формулу:
(3.2.3)
В состоянии - заняты k каналов. Освободиться может любой из этих k каналов с вероятностью μΔt каждый, освобождение любого из k каналов имеет вероятность k μΔt.
Остаться в состоянии k (то есть вероятность не освободиться) равна 1 - k μΔt. Сказанное объясняет, почему в третьем слагаемом фигурирует (k+1) μΔt.
Вероятность к моменту времени t + Δt оказаться в состоянии- определяется выражением:
(3.2.4)
потому что в состоянии заняты все n – каналов, и иначе, чем из них уходить освобождающейся заявке невозможно.
Следующие состояния имеют вероятности (j<m)
(3.2.5)
и, наконец, для последнего состояния имеем
(3.2.6)
Третьего слагаемого здесь нет, так как следующего состояния нет. Кроме того, во втором слагаемом условная вероятность того, что состояние не изменится под действием заявки равна единице, не зависимо от того придет заявка или нет (застав занятую очередь, заявка уйдет в отказ).
Во всех приведенных равенствах раскрываем скобки, переносим соответствующий член влево и делим обе части на Δt. При раскрытии скобок во вторых слагаемых пренебрегаем произведениями, содержащими Δt* Δt.
С
учетом
получаем систему дифференциальных
уравнений
(3.2.7)
Решить систему (3.2.7) численно методом Рунге-Кутта можно, используя функцию rkfixed, реализованную в среде MathCad. Синтаксис обращения к этой функции прост:
Y:=rkfixes(Yo,To,Tf,N,R)
где
Yo – вектор начального состояния;
To, Tf - отрезок интегрирования, который разбивается на
N - шагов:
R- вектор правых частей системы уравнений.
Последний может быть сформирован программой Mathcad, алгоритм которой фактически повторяет запись системы уравнений (3.2.7).
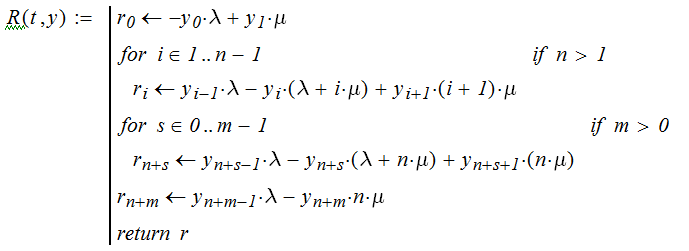
Решение, которое дается этой функцией rkfixes(Yo,To,Tf,N,R), представляет собой матрицу, первый столбец которой есть сеточная функция времени, а остальные столбы определяют вектор неизвестных. Вектор начальных условий может быть сформирован аналогично вектору правых частей уравнения, но достаточно сделать запись
Эта запись формирует вектор начальных условий должного размера, состоящий из нулей и единицей в качестве первого элемента.
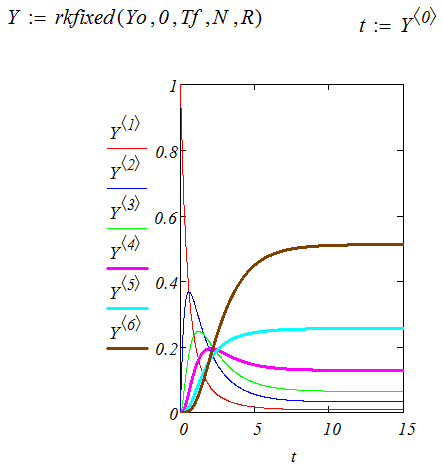
Графики, представляющие решения системы, имеет характерный вид установления стабильного состояния. Этот факт является следствием общей теоремы Маркова.
Примем это утверждение как общее для рассмотренной системы уравнений.
В стационарном состоянии вероятности не меняются, что означает равенство нулю производных в левых частях системы дифференциальных уравнений. Задача поиска вероятностей в стационарном состоянии системы формулируется как задача решения алгебраической системы уравнений. (Для вероятностей в установившемся режиме используем заглавные буквы).
(3.2.8)
Можно
сформировать вектор правых частей
алгебраической системы уравнений по
алгоритму, аналогичному тому, с помощью
еоторого был сформирован вектор правых
частей системы дифференциальных
уравнений для функции Рунге – Кутта.
И затем подобрать значения неизвестных,
при которых этот вектор обращается в
нуль, то есть решить систему
при дополнительном ограничении
.
Это легко выполгняется средставми
MathCad.
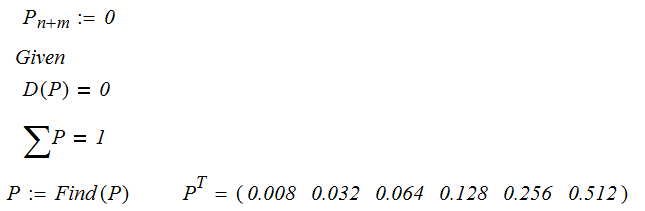
В качестве альтернативы предлагаем общий и легко программируемый способ решения системы (3.2.8), основанный на получении рекуррентных соотношений для вероятностей состояний.
Из первого уравнения получаем
.
Подставляя
во второе уравнение
получим
откуда
Продолжая этот процесс, получим для k <n
Аналогичные действия для n,n+1….n+m дают (j = 1..m)
Полученные
рекуррентные формулы можно записать,
если ввести обозначение
,
ниже следующим образом:
(3.2.9)
С
учетом
, вынося
за скобки, получим
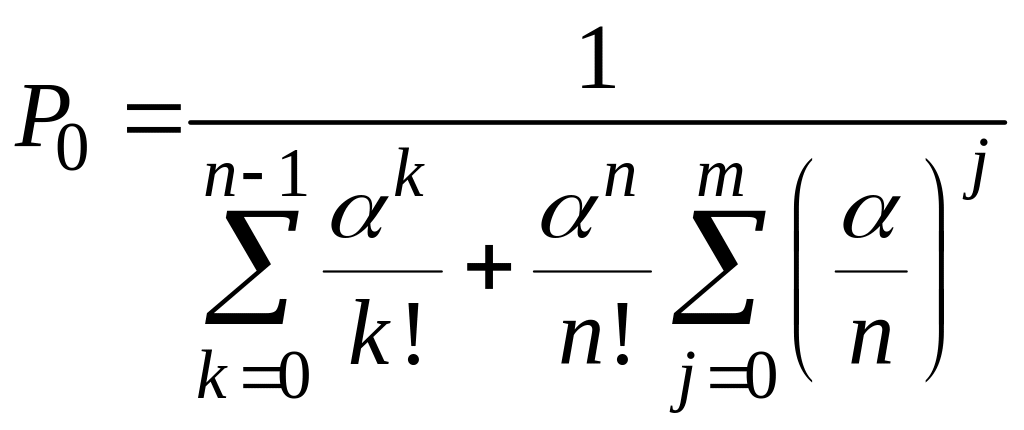(3.2.10)
После вычисления по последней формуле последовательно вычисляется весь вектор P. Приводим программу на MathCad вычислений по формулам (3.2.9) и (3.2.10).
Зная вероятности состояний системы массового обслуживания в установившемся режиме, можно вычислить названные ранее характеристики ее работы.
Вероятность отказа равна вероятности того, что система находится в состоянии n+m и, следовательно, равна .
Вероятность принятия заявки на обслуживание равна
Число заявок, поступающих в единицу времени (интенсивность потока) равно λ. Из их числа доля Pyes обслуживается в системе, и, таким образом, производительность системы равна
Эту производительность обеспечивают каналы, каждый из которых в среднем в единицу времени обслуживает μ заявок. Значит в среднем занято A/ μ каналов.
Подсчитаем среднее число заявок в очереди Lq.
(3.2.11)
Получилась легко программируемая формула. Можно было бы продолжить аналитические выкладки, заметив, что под знаком суммы стоит производная от .
Найдем выражение для среднего времени пребывания заявок в очереди. Если очередная заявка застаёт очередь пустой и имеется хотя бы один свободный канал, то она не ждет вовсе. Если при свободной очереди каналы заняты, то в среднем заявка ждет .
Если заявка застает k-1 заявку ( становится в очередь k-ой), то в среднем она должна переждать всех своих предшественниц плюс своё . Таким образом, среднее время равно . Наконец, если заявка застает в очереди m заявок, то она опять же не ждёт, а уходит необслуженная. Значит, среднее время можно подсчитать по формуле
(3.2.12)
Вспоминая, что выполняется рекуррентное соотношение ,
Используя его в формуле (3.2.12), получим
(3.2.13)
Полученная формула известна как формула Литтла
В заключение приводим формулу для времени пребывания заявки в системе обслуживания. Если заявка принималась на обслуживание, то среднее время обслуживания равно , а если получила отказ, то ее время пребывания в системе равно нулю. Среднее время равно времени . К этому времени надо прибавить среднее, проведенное в очереди Tw. В итоге для среднего времени, проведенного в системе, имеем
(3.2. 14)
ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 12
Простейший поток событий. Показательное распределение. Метод вариация отрезка.
Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени. Примеры: поток вызовов на АТС; поток отказов технической системы; поток самолетов, атакующих охраняемый объект; поток забитых шайб при игре в хоккей и др.
Поток
событий называется стационарным, если
его вероятностные характеристики не
зависят от выбора начала отсчета
времени. Например, вероятность попадания
того или иного числа событий на любой
интервал времени зависит только от
длины этого интервала и не зависит от
того, где именно на оси времени он
расположен. Поток событий называется
ординарным, если вероятность попадания
на элементарный интервал времени
двух или более событий пренебрежимо
мала по сравнению с вероятностью одного
события. Ординарность потока означает,
что события происходят по одиночке, а
не группами. Поток событий называется
потоком без последействия, если число
событий, попавших на любой интервал
(см. рис 5.1) не зависит от того, сколько
событий попало на любой другой не
пересекающийся с ним интервал.
По определению простейший поток событий стационарен, ординарен и не имеет последействия. Этих его свойств достаточно, чтобы вывести законы распределения числа событий и промежутка времени между событиями.
Рассмотрим
распределение числа событий X,
приходящихся
на отрезок времени t.
Разобьем отрезок t
на N
малых промежутков длиною
.
Выберем N
достаточно большим, чтобы в силу
ординарности потока за время
могло произойти не более одного события.
Вероятность
того, что за
произойдет ровно одно событие можно
вычислить, взяв отношение
к математическому ожиданию промежутка
времени между событиями.
Вероятность
того, что за время
не произойдет ни одного события обозначим
.
С точностью до бесконечно малого
Поэтому
Теперь воспользуемся отсутствием последействия и определим вероятность того, что за время t, то есть за N промежутков произойдет ровно X=m событий. Для этого следует воспользоваться формулой биномиального распределения.
Искомое
распределение числа событий
найдем, совершив предельный переход
при
.
Рассмотрим пределы входящих сюда сомножителей.
Таким образом
(5.1)
Это распределение Пуассона. При выводе формулы не использовалось условие стационарности. Поэтому ординарные потоки событий без последействия называются пуассоновскими. Простейший поток - частный случай пуассоновского потока.
Итак, полученная формула определяет вероятность того, что случайное число событий X, которое может произойти за время t, будет равно m. Математическое ожидание и дисперсия случайной величины X равны
Перейдем теперь к рассмотрению распределения случайного промежутка времени T между двумя соседними событиями простейшего потока событий. Обозначим
-
функция распределения случайной
величины T;
-
вероятность того, что за время t очередное
событие не наступило.
-
условная вероятность того, что очередное
событие наступит в промежутке времени
t
при условии, что оно не наступило в
предшествующий отрезок времени t.
-
безусловная вероятность того, что
очередное событие произойдет между
моментами времени t и t+t.
Используя приведенные обозначения, запишем следующее равенство
.
Отсюда
Используя отсутствие последействия и свойство стационарности, найдем что,
Теперь для функции распределения получаем следующее дифференциальное уравнение.
Интегрируя его при начальном условии F(0) = 0, получим функцию распределения случайного промежутка времени между соседними событиями в простейшем потоке событий.
Дифференцируя это выражение, находим плотность распределения промежутка времени
(5.2)
Это известный экспоненциальный закон распределения. Математическое ожидание и дисперсия промежутка времени соответственно равны
Следовательно,
вариация v=1.
2. Агентная модель Т.Шеллинга «Сегрегация».
Данная модель - пионер в области агентного моделирования. Первоначально она была реализована на шахматной доске с монетами в роли черепашек (агентов). В модели имеется два рода агентов. Правила, определяющие поведение индивидуальных агентов, формулировались следующим образом: каждому агенту для «счастья» необходимо, чтобы в его окружении количество агентов другого цвета не превышало некоторый уровень – процент подобных. Иначе агент меняет местоположения (перескакивает ) на свободное место.
Для
представленной реализации модели
количество позиций на доске установлено
равным 9
9. Количество агентов задается слайдером
как четное число, которое делится
пополам, чтобы образовать в равном
числе агентов двух сортов. Процент
однотипных агентов также задается
слайдером и вводит в модель параметр
%-similar-desires.
Фрагмент программы в среде NetLogo, ответственный за содержательную часть модели, содержит процедуры:
to go
if all? turtles [happy?] [ stop ]
move-unhappy-turtles ;двигает «несчастных» на новое место
update-variables
tick
do-plots
end
to move-unhappy-turtles
ask turtles with [ not happy? ]
[ find-new-spot ] ;реализует перемещение поиском нового места
end
to find-new-spot
rt random-float 360
fd random-float 10
if any? other turtles-here найдет свободное место
move-to patch-here ;; в середину пятнышка
end
Результат прогона модели имеет вид:
В конце параграфа приводится полный текст программы, реализующей модель Т.Шеллинга.
Основной вывод, который сделан был автором модели, состоит в том, что даже при высокой степени толерантности (100% - %-similar-wanted) индивидуальных агентов, реальное поведение агентов в массе своей ведет к картине сильной отделённости (сегрегации). Т.Шеллинг использовал данную модель для исследования шаблонов поведения людей при выборе ими места жительства.
Текст программы модели «Сегрегация» на языке NetLogo.
globals [
percent-similar ;; процент соседей , которые той же части
percent-unhappy ;; процент несчастливых
]
turtles-own [
happy? ;;для каждой особи признак указывает, что процент одномастных соседей в пределах желаемого;
similar-nearby ;; сколько рядом мне подобных
other-nearby ;; сколько рядом других
total-nearby ;; сумма двух предыдущих;
]
to setup
clear-all
ask patches [set pcolor gray + 4]
set-default-shape turtles "circle"
if number > count patches
[ user-message (word "В этом пространстве " count patches " не помещается.")
stop ]
;; заселить в случайном месте
ask n-of number patches
[ sprout 1
[ set color brown + 2 ] ]
;; для половины жителей назначить масть иную
ask n-of (number / 2) turtles
[ set color lime ]
update-variables
do-plots
end
to go
if all? turtles [happy?] [ stop ]
move-unhappy-turtles
update-variables
tick
do-plots
end
to move-unhappy-turtles
ask turtles with [ not happy? ]
[ find-new-spot ]
end
to find-new-spot
rt random-float 360
fd random-float 10
if any? other turtles-here
[ find-new-spot ] ;; вызывает себя пока не найдет свободное место
move-to patch-here ;; в середину пятнышка
end
to update-variables
update-turtles
update-globals
end
to update-turtles
ask turtles [
;; встроенная переменная "neighbors" проверяет 8 клеток вокруг
set similar-nearby count (turtles-on neighbors)
with [color = [color] of myself]
set other-nearby count (turtles-on neighbors)
with [color != [color] of myself]
set total-nearby similar-nearby + other-nearby
set happy? similar-nearby >= ( %-similar-wanted * total-nearby / 100 )
]
end
to update-globals
let similar-neighbors sum [similar-nearby] of turtles
let total-neighbors sum [total-nearby] of turtles
set percent-similar (similar-neighbors / total-neighbors) * 100
set percent-unhappy (count turtles with [not happy?]) / (count turtles) * 100
end
to do-plots
set-current-plot "Процент счастливых"
plot percent-similar
set-current-plot "Процент несчастных"
plot percent-unhappy
end
ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 13
Моделирование системы массового обслуживания открытого типа.
Время поступления заявок в систему является случайной величиной. В инструментальных средах «имитационного» моделирования (в том числе и в среде Extendsim 7 Demo) реализованы возможности задавать различные законы распределения этой случайной величины. В данной работе предполагается, что поток заявок является простейшим потоком. Время, которое тратится на обслуживание одной заявки, также предполагается случайной величиной. Моменты завершения обслуживания можно считать потоком событий. За ним закрепилось название - поток обслуживания. В данной работе мы предполагаем, что это простейший поток. Интенсивности потоков заявок и потока обслуживания каналом будем обозначать соответственно λ и μ.
В некоторых инструментальных средах для имитационного моделирования задаются не параметры распределения, а средние времена
и (3.2.1)
Te – среднее время между заявками (entities);
Ts - среднее время обслуживания (service) одним устройством (каналом) одной заявки.
Пусть имеется задача.
Автозаправочная станция имеет две заправочные стойки(n=2). Территория вокруг станции допускает пребывание в очереди на заправку не более m=3 машин. Машины на заправку прибывают с интенсивностью 2 машины в минуту. На заправку в среднем уходит 2 минуты.
В данной задаче заявка – это автомобиль. Канал обслуживания – это заправочная стойка.
Определим основные характеристики системы обслуживания, среди которых:
-вероятность отказа заявки в обслуживании ;
-вероятность выполнения обслуживания ;
-среднее число заявок A , обслуживаемых в единицу времени;
-среднее число занятых каналов обслуживания No;
-среднее число заявок в очереди (средняя длина очереди Lq);
-среднее время ожидания заявки в очереди ;
-среднее время, которое заявка находится в системе Ts (ожидание + время обслуживания); Система может находиться в следующих состояниях:
– все каналы свободны & очередь пуста;
– 1 канал занят обслуживанием & очередь пуста;
……..
– k каналов заняты обслуживанием & очередь пуста ( k < n );
……..
– n каналов заняты обслуживанием & очередь пуста;
– n каналов заняты обслуживанием & в очереди 1 заявка;
……..
– n каналов заняты обслуживанием & в очереди j заявок; (j < m)
……..
– n каналов заняты обслуживанием & в очереди m заявка.
Указанные в перечне состояния имеют вероятности , определить которые и составляет задачу моделирования системы массового обслуживания. Составим уравнения для вероятностей возможных состояний системы.
Если система находится в состоянии – , оставаться в этом состоянии она может, если в течение ближайшего времени (Δt) не поступит новая заявка. Вероятность поступления заявки равна λΔt с точностью до бесконечно-малых по сравнению с Δt.
Если система находится в состоянии – , то перейти в состояние - она может, если в течение ближайшего времени (Δt) занятый канал освободится, вероятность чего равна μΔt с точностью до бесконечно-малых по сравнению с Δt.
Для того, чтобы система перешла за время Δt в состояние-0 из других состояний ( например, из состояния – ) необходимо, чтобы произошло освобождение сразу двух каналов, вероятность этого как произведение двух б.м. величин является б.м более высокого порядка. Поэтому дальше мы рассматриваем переходы только между соседними состояниями.
В результате можно записать, что вероятность системы очутиться в момент времени t + Δt
в состоянии- , выражается равенством:
(3.2.2)
Легко видеть, что формула выражает вероятность суммы независимых событий, каждое из которых есть произведение вероятности на соответствующую условную вероятность.
Для событий от до ( ) получим следующую формулу:
(3.2.3)
В состоянии - заняты k каналов. Освободиться может любой из этих k каналов с вероятностью μΔt каждый, освобождение любого из k каналов имеет вероятность k μΔt.
Остаться в состоянии k (то есть вероятность не освободиться) равна 1 - k μΔt. Сказанное объясняет, почему в третьем слагаемом фигурирует (k+1) μΔt.
Вероятность к моменту времени t + Δt оказаться в состоянии- определяется выражением:
(3.2.4)
потому что в состоянии заняты все n – каналов, и иначе, чем из них уходить освобождающейся заявке невозможно.
Следующие состояния имеют вероятности (j<m)
(3.2.5)
и, наконец, для последнего состояния имеем
(3.2.6)
Третьего слагаемого здесь нет, так как следующего состояния нет. Кроме того, во втором слагаемом условная вероятность того, что состояние не изменится под действием заявки равна единице, не зависимо от того придет заявка или нет (застав занятую очередь, заявка уйдет в отказ).
Во всех приведенных равенствах раскрываем скобки, переносим соответствующий член влево и делим обе части на Δt. При раскрытии скобок во вторых слагаемых пренебрегаем произведениями, содержащими Δt* Δt.
С учетом получаем систему дифференциальных уравнений
(3.2.7)
Решить систему (3.2.7) численно методом Рунге-Кутта можно, используя функцию rkfixed, реализованную в среде MathCad. Синтаксис обращения к этой функции прост:
Y:=rkfixes(Yo,To,Tf,N,R)
где
Yo – вектор начального состояния;
To, Tf - отрезок интегрирования, который разбивается на
N - шагов:
R- вектор правых частей системы уравнений.
Последний может быть сформирован программой Mathcad, алгоритм которой фактически повторяет запись системы уравнений (3.2.7).
Решение, которое дается этой функцией rkfixes(Yo,To,Tf,N,R), представляет собой матрицу, первый столбец которой есть сеточная функция времени, а остальные столбы определяют вектор неизвестных. Вектор начальных условий может быть сформирован аналогично вектору правых частей уравнения, но достаточно сделать запись
Эта запись формирует вектор начальных условий должного размера, состоящий из нулей и единицей в качестве первого элемента.
Графики, представляющие решения системы, имеет характерный вид установления стабильного состояния. Этот факт является следствием общей теоремы Маркова.
Примем это утверждение как общее для рассмотренной системы уравнений.
В стационарном состоянии вероятности не меняются, что означает равенство нулю производных в левых частях системы дифференциальных уравнений. Задача поиска вероятностей в стационарном состоянии системы формулируется как задача решения алгебраической системы уравнений. (Для вероятностей в установившемся режиме используем заглавные буквы).
(3.2.8)
Можно сформировать вектор правых частей алгебраической системы уравнений по алгоритму, аналогичному тому, с помощью еоторого был сформирован вектор правых частей системы дифференциальных уравнений для функции Рунге – Кутта. И затем подобрать значения неизвестных, при которых этот вектор обращается в нуль, то есть решить систему при дополнительном ограничении . Это легко выполгняется средставми MathCad.
В качестве альтернативы предлагаем общий и легко программируемый способ решения системы (3.2.8), основанный на получении рекуррентных соотношений для вероятностей состояний.
Из первого уравнения получаем
.
Подставляя во второе уравнение получим
откуда
Продолжая этот процесс, получим для k <n
Аналогичные действия для n,n+1….n+m дают (j = 1..m)
Полученные рекуррентные формулы можно записать, если ввести обозначение , ниже следующим образом:
(3.2.9)
С учетом , вынося за скобки, получим
(3.2.10)
После вычисления по последней формуле последовательно вычисляется весь вектор P. Приводим программу на MathCad вычислений по формулам (3.2.9) и (3.2.10).
Зная вероятности состояний системы массового обслуживания в установившемся режиме, можно вычислить названные ранее характеристики ее работы.
Вероятность отказа равна вероятности того, что система находится в состоянии n+m и, следовательно, равна .
Вероятность принятия заявки на обслуживание равна
Число заявок, поступающих в единицу времени (интенсивность потока) равно λ. Из их числа доля Pyes обслуживается в системе, и, таким образом, производительность системы равна
Эту производительность обеспечивают каналы, каждый из которых в среднем в единицу времени обслуживает μ заявок. Значит в среднем занято A/ μ каналов.
Подсчитаем среднее число заявок в очереди Lq.
(3.2.11)
Получилась легко программируемая формула. Можно было бы продолжить аналитические выкладки, заметив, что под знаком суммы стоит производная от .
Найдем выражение для среднего времени пребывания заявок в очереди. Если очередная заявка застаёт очередь пустой и имеется хотя бы один свободный канал, то она не ждет вовсе. Если при свободной очереди каналы заняты, то в среднем заявка ждет .
Если заявка застает k-1 заявку ( становится в очередь k-ой), то в среднем она должна переждать всех своих предшественниц плюс своё . Таким образом, среднее время равно . Наконец, если заявка застает в очереди m заявок, то она опять же не ждёт, а уходит необслуженная. Значит, среднее время можно подсчитать по формуле
(3.2.12)
Вспоминая, что выполняется рекуррентное соотношение ,
Используя его в формуле (3.2.12), получим
(3.2.13)
Полученная формула известна как формула Литтла
В заключение приводим формулу для времени пребывания заявки в системе обслуживания. Если заявка принималась на обслуживание, то среднее время обслуживания равно , а если получила отказ, то ее время пребывания в системе равно нулю. Среднее время равно времени . К этому времени надо прибавить среднее, проведенное в очереди Tw. В итоге для среднего времени, проведенного в системе, имеем
(3.2. 14)
2. Нейронные сети и их применение в анализе данных.
схема формального нейрона – простой автомат, который осуществляет преобразование поступающей на его вход данных в результирующий выходной сигнал
Рис. 4.5.1 . Формальный («искусственный» ) нейрон.
Автомат имеет регистр памяти, в которой находятся числа – веса нейрона. Их величина изменяется в ходе обучения нейрона – цепи управления значениями весов на схеме не показаны, хотя они существенны для работы нейрона. Действие, производимое нейроном, состоит в подсчете взвешенной суммы поступающих сигналов. Полученный на выходе блока суммирования сигнал претерпевает преобразование в блоке нелинейного преобразования. Таким образом, работу нейрона можно описать формулой:
(4.5.1)
В этой формуле n – число поступающих на вход сигналов. В качестве функции, осуществляющей нелинейное преобразование, часто используется функция -
(4.5.2)
Параметр γ определяет «крутизну» преобразующей функции. График функции имеет вид-
Рис. 4.5.2 График f(x)
Нейроны являются «строительными кирпичиками» для нейронных сетей. Простейшая сеть – так называемый персептрон или сеть прямого распространения, состоит из последовательных слоев нейронов. Кроме нейронов входного слоя и выходного слоя в сети могут быть внутренние слои. На вход нейронов каждого слоя поступают входные сигналы от всех нейронов предыдущего слоя, Ниже на рисунке 4.5.3 представлена сеть прямого распространения, содержащая один внутренний слой четырьмя нейронами. Сеть предназначена для приема трех входных величин и отправления на выход двух результирующих величин.
Главным их отличием от других методов, например таких, как экспертные системы, является то, что нейросети в принципе не нуждаются в заранее известной модели, а строят ее сами только на основе предъявляемой информации. Именно поэтому нейронные сети и генетические алгоритмы вошли в практику всюду, где нужно решать задачи прогнозирования, классификации, управления - иными словами, в области человеческой деятельности, где есть плохо алгоритмизуемые задачи, для решения которых необходимы либо постоянная работа группы квалифицированных экспертов, либо адаптивные системы автоматизации, каковыми и являются нейронные сети.
Нейросети являются незаменимыми при анализе данных, в частности, для предварительного анализа или отбора, выявления "выпадающих фактов" или грубых ошибок человека, принимающего решения. Целесообразно использовать нейросетевые методы в задачах с неполной или "зашумленной" информацией, особенно в задачах, где решение можно найти интуитивно, и при этом традиционные математические модели не дают желаемого результата.
Рис. 4.5.3. Нейронная сеть прямого распространения.
ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 15
Моделирование системы массового обслуживания закрытого типа.
Системы массового обслуживания, в которых интенсивность потока заявок существенно зависит от состояния самой системы, называются замкнутыми.
Вот примеры таких систем:
Мастера-наладчики (n) обслуживают m станков. При неисправности формируется заявка на ремонт. Понятно, что следующая заявка будет сформирована только после ремонта при новой неполадке.
Экскаватор погружает m самосвалов. Нагруженный самосвал отвозит груз в место назначения и возвращается к экскаватору за следующей порцией. Понятно, что приход самосвала к экскаватору возможен только после того, как самосвал освободится от груза.
Поток посетителей кафе и их обслуживание представляют систему открытого типа, так как приход посетителя не определяется состоянием кафе. Напротив поток посуды от клиентов к мойке образует систему замкнутого типа.
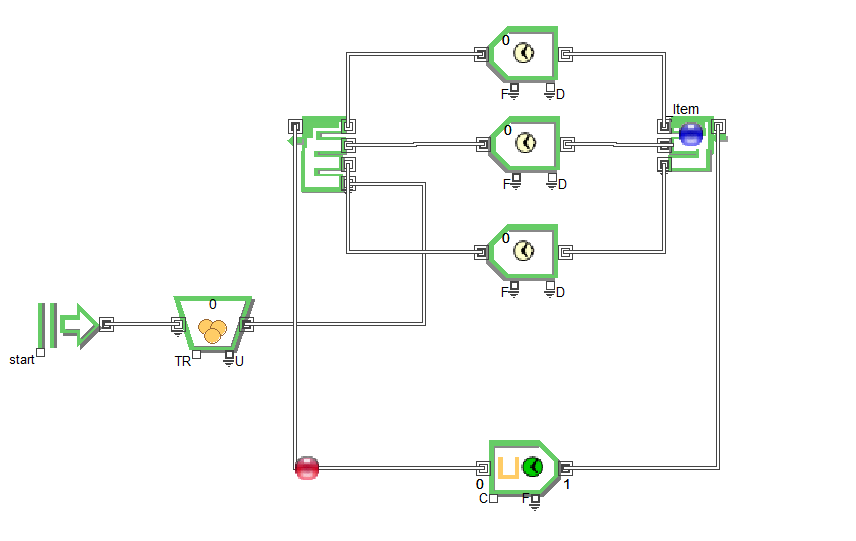
Рис.3.3.2 Закрытая СМО с n =1 и m=3
Пусть имеется m источников заявок и n каналов обработки заявок. В замкнутой системе источник может отправить следующую заявку только после того, как будет обслужена предыдущая. Считаем, что m>n. Состояния системы пронумеруем по количеству заявок, отправленных на обработку.
– все
каналы свободны, ни один источник не
отправил заявку.
– 1
канал занят обслуживанием заявки,
отправленной одним источником.
–
2 канала заняты обслуживанием заявок,
отправленных двумя источниками.
– n
каналов занято обслуживанием,
отправленных n
источниками.
– n
каналов заняты обслуживанием n
заявок, отправленных n
источниками, и одна заявка, отправленная
n+1-ым
источником, ждет обработки.
–
n
каналов заняты обслуживанием n
заявок, отправленных n
источниками, и заявки, отправленные
источниками с n+1
по n+j,
ждут обработки; еще остается m-n-j
источников, способных послать заявку.
– n
каналов заняты обслуживанием n
заявок, отправленных n
источниками, и все заявка, отправленные
источниками с n+1
по
m,
ждут обработки; уже не остается ни
одного источника способного послать
заявку.
Выведем дифференциальные уравнения для вероятностей перечисленных состояний, применив ранее уже использовавшийся метод вариации промежутка времени. Потоки заявок и потоки обслуживания каналами заявок, считаем подчиняющимися экспоненциальному распределению с интенсивностями соответственно λ и μ.
Событие,
состоящее в том, что в момент времени
t+h,
где h
достаточно малый промежуток система
будет находиться в состоянии
складывается из двух событий :
– система находилась в состоянии в момент t, и за время h не пришла заявка ни от одного из m источников;
-система находилась в состоянии в момент t, и канал освободился за время h.
(3.3.1)
То обстоятельство, что имеется m источников, способных послать заявку, обусловило наличие множителя в первом слагаемом формулы.
Для
вероятности состояния
соответствующие выражение будет
содержать три слагаемых – первое
определяется переходом из состояния
в
,
второе отсутствие перехода, а третье
переходом из
в
благодаря освобождению одного из двух
занятых каналов.
(3.3.2)
В состоянии любой из m источников может послать заявку в течение промежутка времени h, в состоянии освободиться может любой из занятых каналов, тогда как остаться в состоянии можно, если не прибудет заявка от m-1 источника способного послать ее и если занятый канал не освободиться за время h.
Запишем соответствующую формулу для вероятностей всех каналов из группы, включающей те состояния, когда все посланные заявки обрабатываются и ни одна не стоит в ожидании.
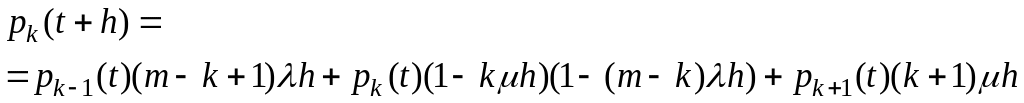(3.3.3)
Здесь k может принимать значения от 1 ( этот случай совпадает с (3.3.2)) до n. Для следующих по номеру состояний, кроме последнего соответствующая формула принимает вид:
(3.3.4)
Для данной группы характерно, что все каналы заняты, и вероятность освобождения канала для всех состояния одинакова, то есть перестает меняться в соответствии с номером, как это было для предыдущей группы. Здесь s меняется от n до m-1.
Для
последнего состояния этой группы
(состояния с номером
)
последнее уравнение запишется в виде:
(3.4’)
В этом состоянии имеет один источник, способный отправить заявку, и все каналы заняты.
Наконец, для последнего состояния, в которое система переходит из состояния если оставшийся источник пошлет заявку, либо не освободится ни один из занятых каналов. В этом состоянии все источники послали заявку и те, которые не попали на обслуживание, ждут:
(3.3.5)
Для каждого из представленных равенств выполняем следующие преобразования: в правой часть раскрываем скобки, переносим влево соответствующий член и делим обе части на h, пренебрегая слагаемыми, содержащими h квадрате. Левая часть при h стремящемся к нулю есть производная, что позволяет получить окончательно дифференциальное уравнение для каждого из состояний.
(3.3.6)
(3.3.7)
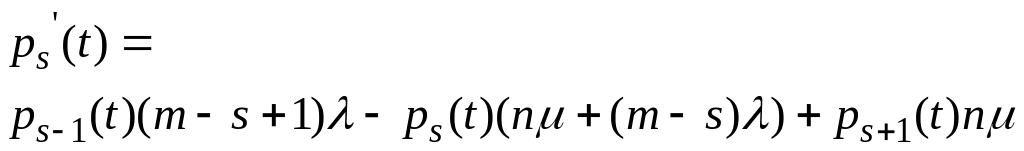(3.3.8)
(3.3.9)
Система может быть решена с использованием численных методов. В инструментальной среде MathCad имеется ряд функций для реализации этих методов, в частности функция rkfixed, в которой реализован метод Рунге-Кутта с фиксированным шагом. Синтаксис обращения к этой функции очень прост;
Rkfixed(Yo,To,T,N,R),
где
Yo - вектор, определяющий начальные условия.
To, T – соответственно начальный и конечный моменты отрезка интегрирования системы уравнений;
R – вектор-функция, задающая правые части системы уравений.
Для формирования последнего можно использовать следующую программу MathCad, не требующую пояснений, потому что повторяет запись системы дифференциальных уравнений:
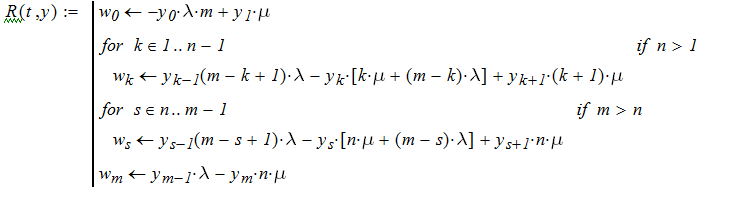
Чтобы воспользоваться данной программой, достаточно задать интенсивности и числа источников и каналов. Например, для n =1 и m =3
при λ= 0.033 и μ=0.1 получаем решения, графики, которых имеют вид:
Вероятности предельных состояний можно определить исходя из условий равенства производных нулю. Полученную систему алгебраических уравнений можно решить в среде MathCad с помощью функции Find. Для того же примера решение получается так:
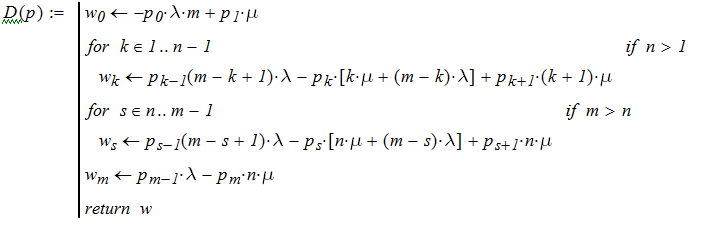
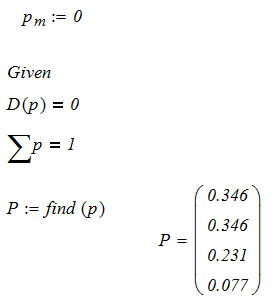
Приводим также формулы для расчета средних значений в установившемся режиме работы СМО.
Среднее число загруженных каналов Nz
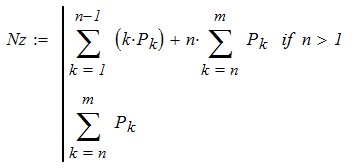
Среднее число A заявок, обслуживаемых системой в единицу времени
Среднее
число поступивших заявок
.
Это следует из того, что величина
есть среднее число источников, чьи
заявки поступают на обслуживание. Это
число, умноженное на
-
среднее число поступающих заявок в
единицу времени, равное A.
Наконец, среднее число заявок, ожидающих обслуживания,
2. Задача Монти-Холла.
Рассмотри задачу [12]:
Есть 3 ящика: "A", "B" и "D", в одном из них приз, в других пусто. Вы выбираете "А". Ведущий точно знает, где приз и сначала открывает заведомо неверный вариант "B", показывая, что ящик пуст. После чего спрашивает, не хотите ли вы поменять свой выбор? Теперь у вас есть возможность остаться при своем варианте "А", либо сменить его на "D".Стоит ли менять свой выбор и почему?
Приз с равной вероятностью может находиться в любом из трех ящиков. Обозначим эти события A1,A2,A3. Выбирая, Вы не знаете где, находится приз, поэтому Ваш выбор никак не связан с событиями А. Вы с равной вероятностью выбираете любой из трех ящиков, и этот факт обозначим B1,B2,B3.
Устроитель розыгрыша знает, где находится приз. Если Вы выбрали один из двух пустых ящиков, устроитель показывает Вам другой пустой и ни в коем случае не тот, где приз. Если Вы выбрали ящик с призом (об этом Вы пока не знаете, но знает устроитель), то устроитель наугад (честно наугад !) выбирает и показывает содержимое одного из пустых ящиков. Условные вероятности действий устроителя при перечисленных условиях- p1,p2,p3 –условные вероятности открыть соответствующий ящик.
D |
A1 |
A2 |
A3 |
B1 |
p1=0 p2=1/2 p3=1/2 |
p1=0 p2=0 p3=1 |
p1=0 p2=1 p3=0 |
B2 |
p1=0 p2=0 p3=1 |
p1=1/2 p2=0 p3=1/2 |
p1=1 p2=0 p3=0 |
B3 |
p1=0 p2=1 p3=0 |
p1=1 p2=0 p3=0 |
p1=1/2 p2=1/2 p3=0 |
Таблица
2.2.1. Условные вероятности выбора пустого
ящика для показа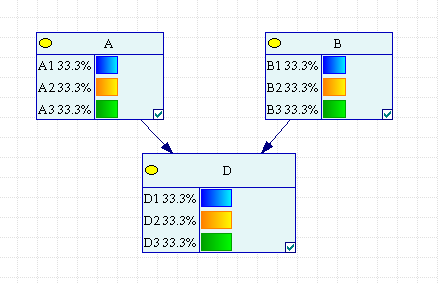
Рис 2.2.1 Байесовская сеть задачи Монти-Холла
До того, как выбор Вами будет сделан, вероятность показать ящики для устроителя одинакова. Условные вероятности для узла D определим в соответствии с Таблицей 2.2.1.
Рис. 2.2.10 Условные вероятности показать пустой ящик в GINIE 2.0
Допустим Вы выбрали первый ящик.
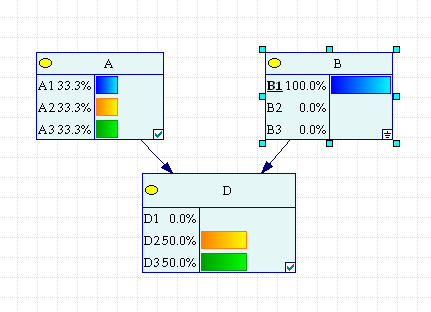
Рис.2.2.2 Случай выбора первого ящика.
В соответствии с таблицей условных вероятностей этот факт отразился в узле D. Вероятность выбрать для показа указанный Вами ящик естественно равна нулю. Устроитель наугад выбирает любой из двух пустых с равными вероятностями. Пусть он показал второй. Его выбор по теореме Байеса привел к переоценке вероятностей гипотез о месте приза. Видно, что вероятность приза больше не в той коробке, которую Вы указали.
Эксперименты с другими вариантами Вашего и устроителя выбора дадут тот же эффект.
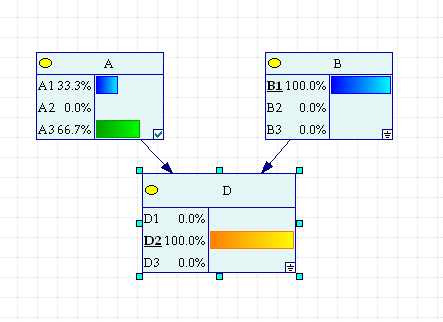
Рис.2.2.3 Устроитель показывает пустой второй ящик.
Рис.2.2.4. Устроитель показал третий ящик.
Если на Ваш выбор устроитель демонстрирует пустой третий ящик, то апостериорные вероятности опять в пользу смены Вашего выбора.
Если выбран первый ящик, а приз находится во втором, и устроитель соответственно показал третий, то расчет непосредственно по формуле Байеса дает:
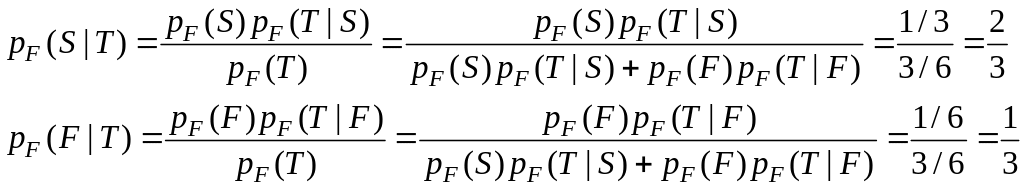
Это апостериорные вероятности того, что приз во втором или в выбранном ранее первом ящике. Аналогично просчитываются и все остальные случаи.
Итак, правильным ответом к этой задаче является следовать совету устроителя и изменить свой первоначальный выбор.
Простое объяснение этого ответа состоит в следующем соображении. Для того, чтобы выиграть приз без изменения выбора, игрок должен сразу угадать ящик, в котором приз. Вероятность этого равна 1/3. Если же игрок первоначально выбирает пустой ящик, (а вероятность этого события 2/3, поскольку есть два пустых ящик и один с призом), то он может однозначно получить приз, изменив своё решение, так как остаются приз и пустой ящик, открытый устроителем. Таким образом, без смены выбора игрок остаётся при своей первоначальной вероятности выигрыша 1/3, а при смене первоначального выбора, игрок оборачивает себе на пользу в два раза большую оставшуюся вероятность того, что сначала он не угадал.
Еще одно пояснение. Переформулируем задачу: честный устроитель объявляет игроку, что в одном ящике приз, и предлагает ему сначала выбрать ящик, а после этого выбрать одно из двух действий: открыть ящик (в старой формулировке это называется "не изменять своего выбора") или открыть два других (в старой формулировке это как раз и будет "изменить выбор"). Ясно, что игрок выберет второе из двух действий, так как вероятность получения приза в этом случае в два раза выше. А та мелочь, что ведущий еще до выбора действия "показал пустой ящик ", никак не помогает и не мешает выбору.
Рассмотренная задача хорошо иллюстрирует возможности Байесовских сетей, а также является достаточно яркой иллюстрацией вероятностных рассуждений, при которых осуществляется поиск вариантов, максимизирующих вероятность вариантов выбора. Однако необходимо помнить, что оптимизация при вероятностных рассуждениях, не эквивалентна успешности выбора. Хороший пример в романе «12 стульев» И.Ильфа и А.Петрова, где Великий Комбинатор, руководствуясь вероятностными соображениями, отправляется в погоню за 9 стульями против одного, тогда как в нём как раз и был приз. Вероятностные модели и рассуждения смыкаются с фактами в области статистики и получают смысл как средние результатов многочисленных повторений.
ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 16
Построение модели классификатора в форме «дерева решений».
Пример дерева решений приведен на рисунке 4.6.2. Принята форма изображения дерева, когда корень сверху, а терминальные вершины – «листья» снизу, Но также привлекательна и форма дерева построенного в системе Deductor и изображенная на рисунке 4.6.3. Оба рисунка относятся к одной и той же задаче – построение набора решающих правил, выражающих принадлежность объектов к определенному классу в зависимости от значений свойств этих объектов. Данный набор строится на основе ряда прецедентов (примеров) и, по сути, представляет собой отображение (регрессию) атрибутов на некоторое данное, которое характеризует класс объекта. Пусть имеется таблица, которая является извлечением из журнала регистрации игры в гольф.
OUTLOOK |
TEMPERAT |
HUMIDITY |
WINDY |
PLAY |
sunny |
85 |
85 |
false |
Don'tplay |
sunny |
80 |
90 |
true |
Don'tplay |
overcast |
83 |
78 |
false |
Play |
rain |
70 |
96 |
false |
Play |
rain |
68 |
80 |
false |
Play |
rain |
65 |
70 |
true |
Don'tplay |
overcast |
64 |
65 |
true |
Play |
sunny |
72 |
95 |
false |
Don'tplay |
sunny |
69 |
70 |
false |
Play |
rain |
75 |
80 |
false |
Play |
sunny |
75 |
70 |
true |
Play |
overcast |
72 |
90 |
true |
Play |
overcast |
71 |
75 |
false |
Play |
rain |
71 |
80 |
true |
Don'tplay |
Таблица 4.6.1. Данные об игре в гольф.
Задача состоит в том, чтобы выразить данное PLAY (категориальное данное, метка класса, результирующее данное, выходное) через значения атрибутов (OUTLOOK –погода,TEMPERATURE – не требуется перевод, HUMIDITY – влажность, WINDY- отвечающее за наличие или отсутствие ветра на площадке в гольф и, как всякое логическое данное, имеет вопросительный модус – ветрено? - «ответ в латинице – true или false»).
Значение категориального данного выражает решение об отнесении объекта (в примере, таким объектом является игра и соответствующая ей строка в таблице) к классу Play или к классу Don’t play . Этот намек на то, почему классификационное дерево получило название дерево решений. Если перечень значений атрибутов считать вопросом - играть или не играть, то в исходной таблице (обучающей) ответ известен. При появлении новых условий и, соответственно, новых вопросов, дать ответ позволяют правила, построенные по обучающей выборке.
Если в новом объекте значение признака OUTLOOK = sunny , то это означает, что объект по этому свойству похож на те объекты из обучающей выборки, которые имеют ту же характеристику.
OUTLOOK |
TEMPERAT |
HUMIDITY |
WINDY |
PLAY |
sunny |
85 |
85 |
false |
Don'tplay |
sunny |
80 |
90 |
true |
Don'tplay |
sunny |
72 |
95 |
false |
Don'tplay |
sunny |
69 |
70 |
false |
Play |
sunny |
75 |
70 |
true |
Play |
|
|
|
|
|
OUTLOOK |
TEMPERAT |
HUMIDITY |
WINDY |
PLAY |
overcast |
83 |
78 |
false |
Play |
overcast |
64 |
65 |
true |
Play |
overcast |
72 |
90 |
true |
Play |
overcast |
71 |
75 |
false |
Play |
OUTLOOK |
TEMPERAT |
HUMIDITY |
WINDY |
PLAY |
rain |
70 |
96 |
false |
Play |
rain |
68 |
80 |
false |
Play |
rain |
65 |
70 |
true |
Don'tplay |
rain |
75 |
80 |
false |
Play |
rain |
71 |
80 |
true |
Don'tplay |
Видно, что ясного однозначного ответа на вопрос быть или не быть игре мы не получаем. В других случаях, например, когда OUTLOOK = overcast (облачно, солнце не палит, ветра нет, дождя нет) ответ получается однозначным - Play.
Мы получили способ отображения атрибутов в метку класса – разбить исходную совокупность на однородные подмножества однородные по категориальному признаку.
Построение дерева решений (как и дальнейшее использование его для классификации новых объектов) основывается на последовательном выборе признака и разбиении исходной совокупности обучающих прецедентов по значениям этого признака. Выбор признака для очередного дробления осуществляется по критерию максимизации однородности получающихся подмножеств. Придумано несколько таких критериев, мы рассмотрим информационный критерий. Исходная неоднородность категориального признака (метки класса - PLAY) -
(4.6.1)
В
формуле (4.6.1) n
– число значений метки класса (в нашем
примере n=2),
-
доля объектов с определенным значением
метки класса. В таблице 4.6.1
Разбиение исходной выборки по признаку OUTLOOK создает три подмножества, каждое из которых обладает своей мерой неопределенности, которую оно вносит в суммарную неопределенность с весом равным доле подмножества в родительском множестве.
NegINF(OUTLOOK)=Psunny*NegINF(sunny)+
+Povercast*NegINF(overcast)+Prain*NegINF(rain)
Подсчет неопределенности в каждом из подмножеств проводится по формуле (4.6.1).
Если подмножество получилось однородным как в случае OUTLOOK= overcast, то неопредленность NegINF(overcast)=0.
Для таких подмножеств дальнейшее деление не производится, и это подмножество становится листом на дереве решений. Если подмножество неоднородно, то оно подвергается дальнейшему делению по одному из оставшихся признаков, причем тот выбирается из тех же соображений -максимального увеличения неопределенности. Деление может быть заблокировано, если размер подмножества меньше некоторой заданной границы (например, граница 2) или вступают в силу соображения о сокращении (Pruning) ветвистости дерева с целью улучшить его зрительное восприятие.
Уменьшение неопределенности, получившееся в результате разбиения на подмножества, может быть понято как то, что знание о подмножестве уже увеличивает возможность предсказания какого класса этот объект.
Информационный выигрыш в результате разбиения по признаку OUTLOOK
GainINF(OUTLOOK)= 0.94-0.694 = 0.246.
Для сравнения, если бы в качестве признака для деления на подмножества был выбран признак (атрибут) WINDY , то выигрыш составил бы
GainINF(WINDY) =0.048.
Из сравнения этих двух признаков следует, что предпочтение надо отдать первому, так как разбиение по нему существенно сильнее уменьшает неопределенность.
При оценке числовых признаков на предмет того, как разбиение на подмножества влияют на неопределенность, можно осуществить разделение по критерию меньше или больше значение признака некоторой границы. В качестве границы можно принять медиану разброса значений этого признака в выборке. Но в большинстве инструментальных средств, включающих в себе построение дерева решения, граница выбирается следующим образом – она подбирается так, чтобы обеспечить максимальный выигрыш при разбиении выборки по этому признаку. В системе Deductor даже строится график зависимости выигрыша от выбранной границы разбиения. После выбора границы и определения неоднородности полученных подмножеств производится сравнение с выигрышами от других признаков. Для нашего примера расчеты показали, что GainINF(TEMPERATURE) и GainINF(HUMIDITY) заметно меньше.
В великолепных инструментальных системах для анализа данных (data mining), таких как Deductor(www.basegroup.ru) , RapidMiner (Yale University) в качестве критерия берется не информационный выигрыш, а он же, но с поправкой, – так называемый GainRatio.
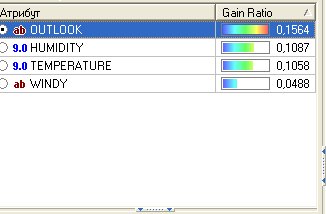
Рис. 4.6.1 Сравнение признаков при определении разбиения исходной выборки.
Определение критерия GainRatio :
(4.6.3)
Коррекция исходного критерия делением на величину SplitInfo(X), обусловлено стремлением уменьшить выигрыш для признаков, имеющих много уникальных значений типа порядковый номер записи. Такие признаки, как правило, имеют большую энтропию NegINF и после деления на подмножества (в случае номеров – это единичные подмножества) их энтропия уменьшается до нуля. Если не производить коррекцию, то такие признаки будут выбираться в первую очередь и дерево потеряет смысл. Коэффициент SplitInfo(X) вычисляет неопределенность исходного множества не по признаку класса (PLAY, в примере), а признаку – кандидату на деление.
Например, для признака OUTLOOK величина
где - доля объектов с заданным значением атрибута в исходной выборке.
Для признака OUTLOOK расчет дает
Поэтому
Gain
Ratio
для этого признака равен
.
По этому критерию и проводится сравнение
атрибутов при выборе очередного признака
для деления (рис. 4.6.1). Если некоторое
данное состоит из N
уникальных значений, то для него
-
информация по Харди с минусом.
Для
этого данного Gain
Ratio(N)
будет не
,
а 1. Но обычно его сразу исключают из
списка претендентов на то, чтобы быть
разделяющим.
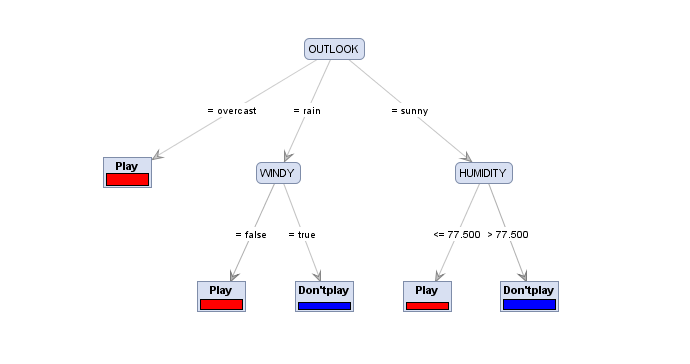
Рис. 4.6.2 Классификатор - дерево решений для задачи.
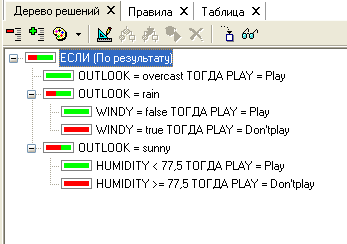
Рис. 4.6.3 Классификатор – дерево решений из системы Deductor.
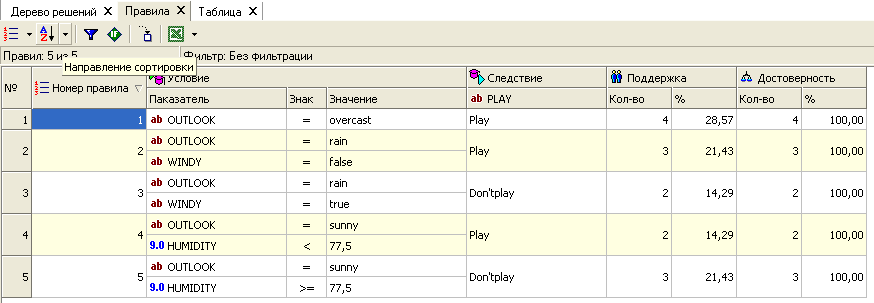
Рис. 4.6.4 Классификатор в форме правил
Перед тем как перейти к режиму использования дерева решений как классификатора новых объектов, рассмотрим элементы полученного дерева- узлы, вершина, листы и дуги.
Вершина дерева, узлы – очередное (вначале исходное) множество объектов обозначается атрибутом, по которому производится разбиение. Листы представляют конечный результат деления множества на подмножества. В идеале – это однородное по метке класса подмножество. Если в конечном узле не однородное подмножество, то правило отнесения объекта к классу имеет вероятностные меры. На дуге записывается выбор значения в узле.
Вероятностные характеристики правила – это достоверность и поддержка. Поддержка – это доля объектов в терминальном узле по отношению к исходной выборке. Достоверность – это доля объектов с некоторой меткой класса в терминальном подмножестве по отношению к численности объектов в нем. На рис. 4.6.4 выписаны правила вместе с вероятностными характеристиками. Для нового объекта дерево просматривается от вершины к листам, проходя по ответам на вопросы, задаваемые в узлах: OUTLOOK = sunny и т.п. и дальше переход в зависимости от ответа.
В итоге найденный терминальный узел (лист), представляющий класс, в который попали объекты с аналогичными свойствами, дает решение – ответ на вопрос к какому классу относится новый объект.
Объяснение «парадокса Симпсон».
Два студента A и B, проходят тесты по математике. Каждому дается выбор из 100 задач. A выполняет 68 заданий из ста, а B - 75.
Кажется, что B лучше знает предмет, чем A. Однако задания теста условно можно разделить на два раздела. A выбирает задачи повышенной трудности, а B отдает предпочтение стандартным задачам.
Из 20 задач стандартного уровня трудности A правильно решил 18 задач, а B из 80 задач добился успеха в 65 случаях. Выходит, что A добивался успеха в 90% случаев, а B - в 81% случаев, поэтому A лучше знает предмет, чем B. Повышенной трудности задачи A пытался решать 80 раз, и справился в 50 случаях, то есть в 62.5%. Со своей стороны B пытался отличиться с трудными заданиями 20 раз, и вышло у него всего в 10 из них - 50%. Выходит, что A лучше знает предмет и по разделу повышенной трудности
Но A правильно отвечал 68 раз из ста, а B 75 раз из ста, так что же, получается, что B должен был получить более высокую оценку A?
Если не учитывать трудность заданий, на основании сравнения 68/100 и 75/100, мы приходим к ошибочному заключению . Но внутри вопроса таится скрытая переменная – уровень трудоемкости задания - которая коренным образом меняет то, как надлежит интерпретировать результаты.
F –это принадлежность задачи к типу повышенной трудности
~F- это принадлежность задачи к стандартному типу
P(E|A) > P(E|B)
P(E|A, F) < P(E|B, F)
P(E|A,~F) < P(E|B,~F)
Парадокс Симпсона это обращения знака неравенства на противоположный при объединении двух подмножеств.
Все задачи |
Решено |
Нерешено |
Итого |
Процент |
Оценка |
A |
75 |
25 |
100 |
75% |
Выше |
B |
68 |
32 |
100 |
68% |
Ниже |
Трудные задачи |
Решено |
Нерешено |
Итого |
Процент |
Оценка |
A |
10 |
10 |
20 |
50% |
ниже |
B |
50 |
30 |
80 |
62.5% |
выше |
Стандартные |
Решено |
Нерешено |
Итого |
Процент |
Оценка |
A |
65 |
15 |
80 |
81.3% |
ниже |
B |
18 |
2 |
20 |
90% |
выше |
Таб. 2.5.1. Данные, иллюстрирующие парадокс Симпсона.
На рис. 2.5.1 представлена байесовская сеть для визуализации условий «парадокса» Симпсона.
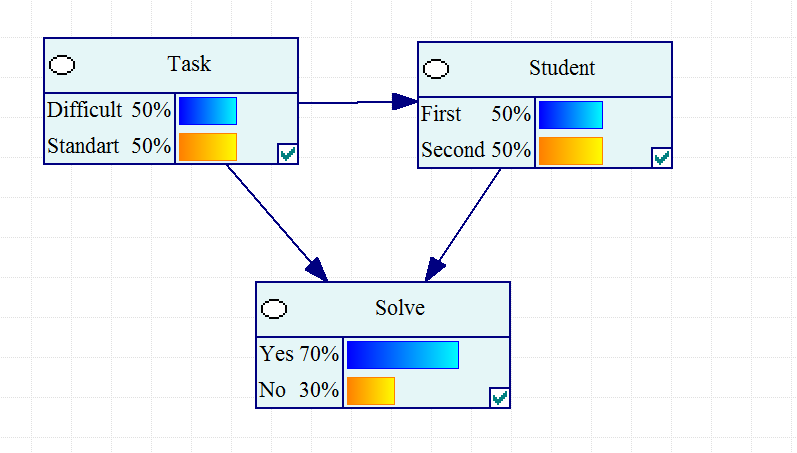
Рис. 2.5.1. «Парадокс» Симпсона .
Изменяя действующее лицо мы не только получаем соотношение решенных задач. Но выясняем , что нет никакого парадокса , а есть скрываемая переменная – трудоемкость задач, разное количество которых приводит к видимости парадокса.
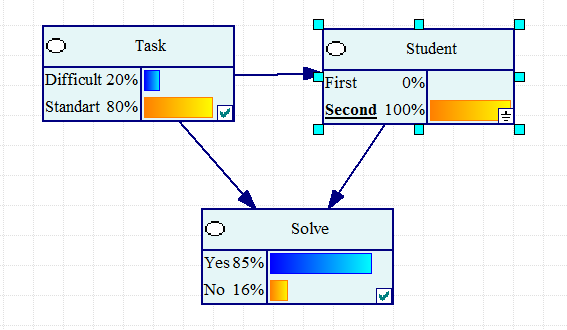
Рис. 2.5.2. Второй студент предпочитает стандартные задачи.
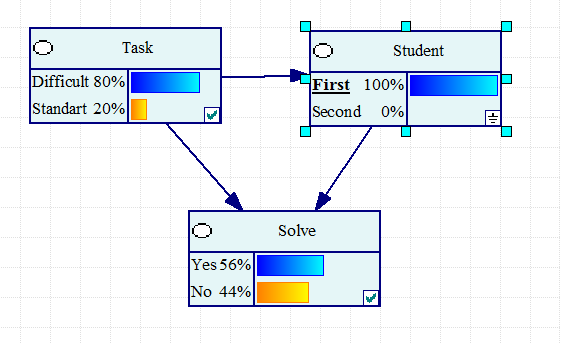
Рис. 2.5.3.. Первый студент не боится трудных задач