14.3. Несколько простых модификаций метода эйлера

Разовьем последний из подходов к построению метода Эйлера. Очевидно, применение к интегральному равенству (14.13) других простейших квадратурных формул будет порождать новые методы численного интегрирования задачи Коши (14.1)-(14.2).

Так, если в (14.13) использовать простейшую квадратурную формулу правых прямоугольников (12.7), придем к методу

y_i+1 = У_i +hf(x_i+1, y_i+1), i = 0,1,.... n. (14.14)

Этот метод называют неявным (или обратным) методом Эйлера, поскольку для вычисления неизвестного значения У_i+1 ≈ у(х_i+1) по известному значению у_i ≈ у(х_i) требуется решать уравнение, в общем случае нелинейное. Имеет ли свою сферу применения подобный метод, порядок которого такой же,

как и у явного метода Эйлера (14.8) (первый), и один шаг вычислений по которому столь трудоемок? Положительный ответ на этот вопрос будет дан в гл. 16.

Применение к интегралу в (14.13) простейшей квадратурной формулы трапеций (12.26) приводит тоже к неявному методу

(14.15)

который будем называть методом трапеций. Квадратурная формула трапеций, как известно из гл.12, на порядок точнее формул левых и правых прямоугольников. Отсюда вытекает более высокий (на единицу) порядок точности метода трапеций (14.15) по сравнению с явным и с неявным методами Эйлера (14.8) и (14.14), т.е. метод трапеций (14.15) — это метод второго порядка (впоследствии, в § 15.4, к этому выводу придем из других соображений).

Некоторый интерес представляет совместное применение явного метода Эйлера и неявного метода трапеций.

По форме равенство (14.15) представляет собой скалярную задачу о неподвижной точке относительно неизвестного значения у_i+1. Поэтому, если в правую часть (14.15) подставить хорошее начальное приближение У_i+1, подсчитываемое по формуле (14.14), то тогда само это равенство можно считать шагом метода простых итераций для уточнения этого значения (см. гл.6). Таким образом, получаем гибридный метод

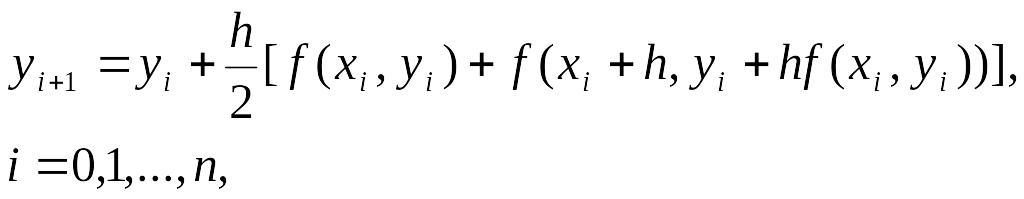
который называют методом Хойна [6, 60] (или Хъюна [138]).

(14.16)

Ясно, что можно достичь большей точности, если, исходя из того же начального приближения

,

сделать не одну, а несколько итераций по методу трапеций:

(14.17)

Такой вариант совместного применения метода Эйлера и метода трапеций называют усовершенствованным методом Эйлера-Коши [84] с итерационной обработкой '. Делать много итераций по формуле (14.17) не рекомендуется (обычно их выполняют не более трех-четырех). Совпадение определенного числа разрядов в полученных числах и говорит о точности, с которой решено методом простых итераций уравнение (14.15) относительно y_i+1, а вовсе не о том, что с такой точностью найдено значение y(x_i+1).

Чтобы получить, следующую модификацию метода Эйлера, проинтегрируем уравнение (14.1) по отрезку [x_i-1, x_i+1]. Имеем

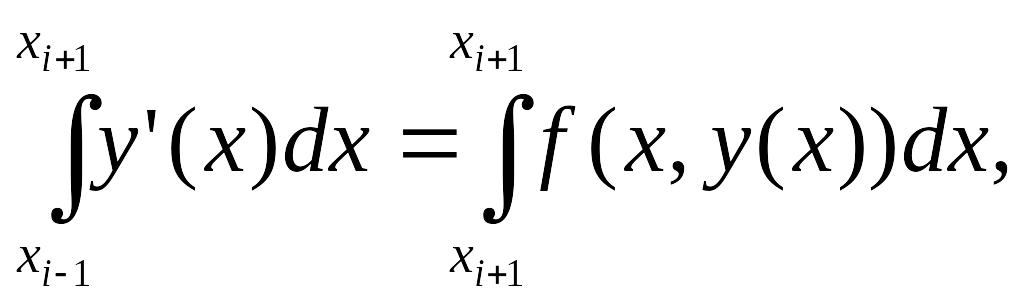
откуда следует равенство

,

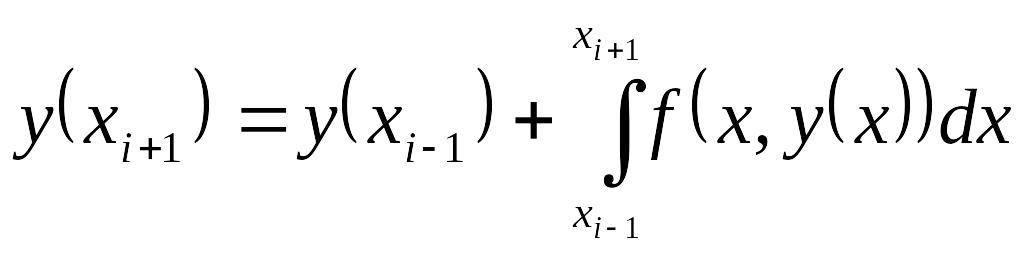Применяя к последнему интегралу одноточечную квадратурную формулу средних прямоугольников (12.10) и заменяя значения y(x_i-1) и y(x_i) известными приближенными значениями y_i-1 и y_i соответственно, из (14.18) выводим формулу для подсчета приближенного значения y(x_i+1)

y_i+1=y_i-1+2hf(x_i,y_i), i = 1,2,...,n-1, (14.19)

которую будем называть уточненным методом Эйлера [58].

Как известно, квадратурная формула прямоугольников (средней точки) имеет тот же порядок точности, что и квадратурная формула трапеций, так что уточненный метод Эйлера (14.19) тоже является методом второго порядка. Подтверждением этого факта может служить вывод метода (14.19) на разностной основе. Применив к равенству (14.11) формулу симметричной аппроксимации y'(x_i) второго порядка точности, получим

,

откуда после приближенной замены y(x_i-1) ≈ y_i-1, y(x_i)≈y_i , y(x_i+1) ≈ y_i+1 следует (14.19).

Обратим внимание на одно принципиальное отличие метода (14.19) от всех других рассмотренных до этого момента методов: метод (14.19) является двухшаговым. Здесь для вычисления значения y_i+1 привлекаются два предыдущих значения у_i, и y_i-1 . Двухшаговость накладывает определенные ограничения, по крайней мере, на начало численного процесса: значение y₁ ≈ у(x₁) не может быть найдено непосредственно этим методом с тем же шагом h. Поэтому недостающую вторую начальную для процесса (14.19) точку приходится получать другим путем, например, явным методом Эйлера, а чтобы не сделать сразу большой ошибки, применяя на старте метод более низкого порядка точности, рекомендуется осуществлять постепенное вхождение в процесс (14.19). Так, «разгон» можно выполнить по формулам

(14.20)

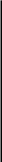а далее уже переключаться на счет по формуле (14.19).

Пример 14.1. Рассмотрим простое линейное уравнение

у' = 2х-3у

с начальным условием y(0) = 1. На этой задаче легко проследить за вычислениями, реализующими различные выведенные выше методы. Знание ее точного решения позволяет провести сравнение результатов приближенных вычислений по разным формулам с ис­тинным решением и проверить, насколько соответствуют представления о точности тех или иных методов тому, что наблюдается в данном, навер­ное, далеко не самом типичном частном случае.

Сначала сделаем несколько последовательных приближений по ме­тоду Пикара. Его итерационная формула (14.5) для данной начальной за­дачи имеет вид

.

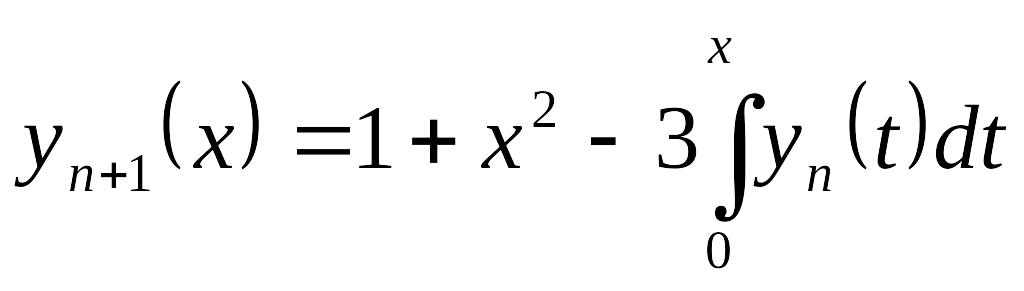Подставляя сюда у₀ = 1, при п = 0,1, 2 последовательно получаем:

Эти результаты удобно сравнить с точным решением, если в последнем разложить в ряд по степеням х фигурирующую там функцию е^-3x. Тогда получим представление решения в виде ряда

с которым, как видим, хорошо согласуются приближения у₁,,y₂,y_з, определяемые методом Пикара.

Теперь проведем подсчет приближенных значений решения у(х) данной задачи в точке х = 0.2 численным методом Эйлера и его модификациями, принимая h = 0.1 (т.е. за два шага). Результаты этих вычислений и фактические ошибки, найденные сравнением с точным значением у(0.2) = 0.581881..., отражены в следующей таблице.

Метод	y1≈y(0.1)	у2≈у(0.2)	y(О.2)-y2
Эйлера (14.8)	0.7	0.51	≈0.07
Неявный Эйлера (14.14)	≈0.7846	≈0.6343	≈-0.05
Трапеций (14.15)	≈0.7478	≈0.5788	≈ 0.003
Хойна (14.16)	0.755	≈0.5895	≈-0.008
Уточненный Эйлера (14.19)-(14.20)	0.755	0.587	≈ -0.005

Последний столбец в этой таблице со всей очевидностью показывает большую точность методов второго порядка (см. три последних строки).