Метод опорных векторов в задаче классификации.

Пусть имеется набор учебных примеров, каждый из которых имеет два числовых параметра и отнесенных к одному из классов y = {-1,1}:

x1	x2	y
0	1	1
1	2	1
2	0	1
3	3	-1
3	4	-1
5	4	-1

Таблица 4.5.1. Учебные примеры для классификатора

На рис.4.5.1 классы отображены цветом так, что класс 1 закрашен белым цветом, а класс -1 –черным.

На рис. 4.5.2 показаны несколько прямых разделяющих классы.

Рис.4.5.1 Пример обучающей выборки из таблицы 4.5.1

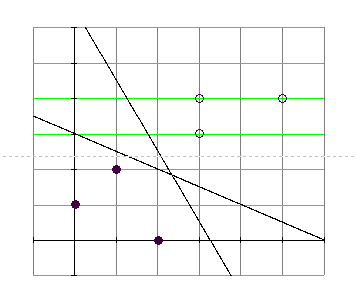
Рис. 4.5.2 Прямые, разделяющие классы

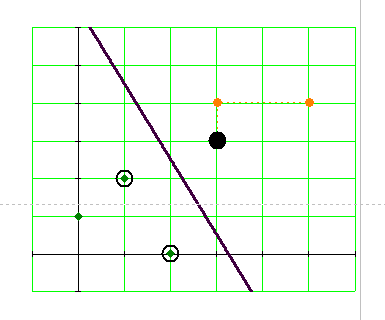
Рис. 4.5.3. Опорные векторы.

Одной из разделяющих линий соответствует разделяющая полоска наибольшей ширины. Точки, касающиеся полоски разделения и обведенные кружочками, – «опорные вектора»

Согласно известному факту из аналитической геометрии расстояние от точки на плоскости до прямой, заданной уравнением , выражается формулой

(4.5.1)

Расстояние имеет знак, причем точки, расположенные по разные стороны прямой, имеют разные знаки. Выбор знака зависит от знака коэффициентов уравнения прямой, и если поменять знак, то точки на плоскости, имевшие знак плюс, получат знак минус и наоборот.

Обозначим ширину разделяющей полоски на рисунке 4.5.3 буквой ρ. Для расстояний от прямой до точек «светлого класса» выполняется неравенство (чем дальше, тем расстояние больше, так как оно выбрано положительным):

(4.5.2)

Для точек «черного» класса выполняется неравенство (чем дальше, тем расстояние меньше, так как оно выбрано отрицательного знака):

(4.5.3)

Эти два неравенства можно объединить в одно, учитывая знак, используемый для обозначения класса (умножение на -1 изменяет знак неравенства)

(4.5.4)

поскольку мы принимаем, что

для чёрных точек, и (4.5.5)

для белых точек. (4.5.5’)

На основании данной обучающей выборки должен быть построен классификатор, который будет определять класс точек по их координатам, Доказано, и это интуитивно ясно, что чем шире разделяющая полоса (то есть, чем больше ρ), тем меньше риск допустить ошибку в случае, если координаты «новой точки» задаются с погрешностью.

Это соображение приводит к задаче оптимизации с учетом ограничений:

при

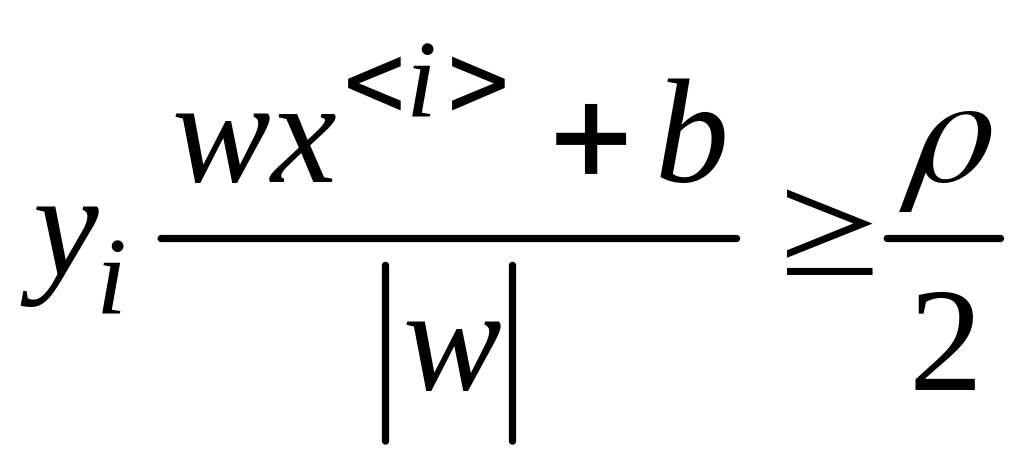
(4.5.6)

Здесь n – общее число точек (примеров в обучающей выборке).

В силу того, что мы можем по желанию выбирать нормирующий множитель в (4.5.2), установим его равным

(4.5.6’)

Тогда задача (4.5.6) формулируется в виде:

при

(4.5.7)

Используя множители Лагранжа , получим функцию Лагранжа задачи оптимизации (4.5.7).

(4.5.8)

Принято множители Лагранжа считать положительными и выбирать знак минус перед суммой с ограничениями. Доказывается в теории выпуклого программирования, что решению задачи соответствует седловая точка функции Лагранжа, доставляющая минимум по параметрам прямой и максимум по множителям Лагранжа.

Необходимые условия минимума L:

(4.5.9)

Первые уравнения из (4.5.9) подставляем в Лагранжиан (4.5.8) и получим с учетом последнего

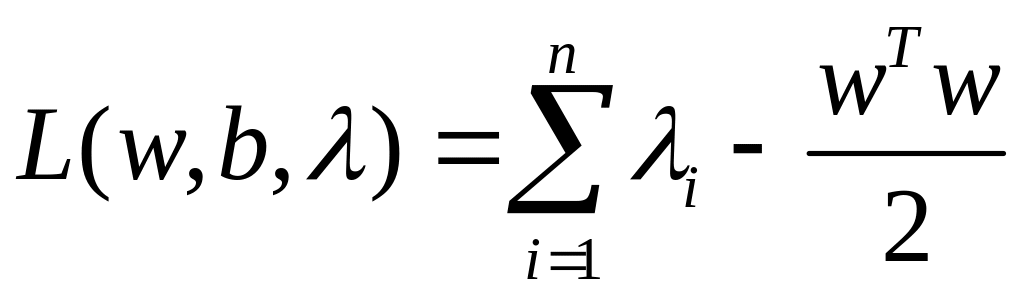
(4.5.10)

Получилась так называемая дуальная форма Лагранжиана, который зависит теперь только от множителей. Ей соответствует задача оптимизации:

(4.5.11)

при ограничениях и (4.5.12)

Полученная задача является задача квадратичной оптимизации при линейных ограничениях. Существуют эффективные программные средства для её решения. Например, в MathCad решение может быть получено с помощью простой записи:

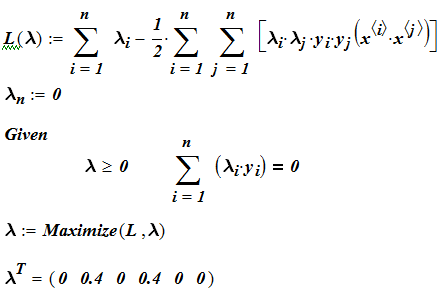
Далее полученные множители подставляем в (4.5.9) , чтобы получить w, b и из них (4.5.6’).

(4.5.13)

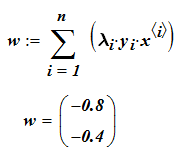
Свободный член уравнения прямой определим из условия, что расстояния от опорных точек (для которых множитель Лагранжа не равен нулю) до искомой прямой должны быть равны и противоположны по знаку.

Для опорного вектора s соотношение (4.5.7) выполняется как точное равенство.

Последнее равенство можно записать, используя (4.5.13)

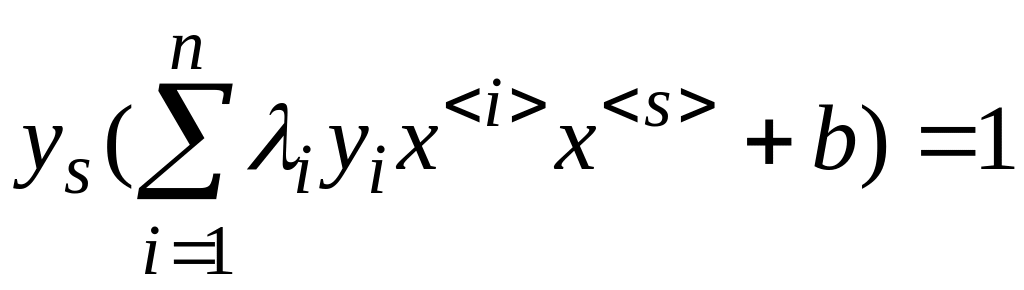
Если умножить обе части последнего равенства на , то получаем

, откуда

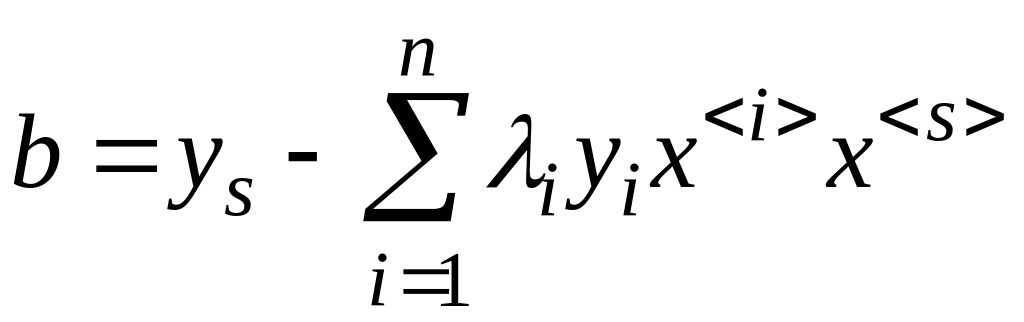для произвольного опорного вектора s.

При программировании вычислений удобно брать не произвольный вектор, а среднее по опорным векторам.

(4.5.14)

На MathCad это может быть выполнено с помощью записи (предварительно приводим уравнение прямой к нормальной форме, тогда подстановка координат точек сразу даст расстояние):

_{Окончательно, ширина полосы разделения}

Классифицирующая функция может быть теперь записана в виде функции, определяющий знак полуплоскости в которой окажется классифицируемый объект:

(4.5.15)

Здесь суммирование производится по опорным векторам, для которых λ больше нуля.

Пусть теперь в обучающей выборке точки не разделены.

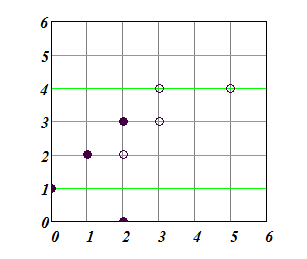
Рис. 4.5.4 Пример обучающего множества с линейно неразделяемыми классами.

Вместо «жёстких» условий разделения классов

принимаем «смягчение» границ:

и объединяем их в одно

(4.5.16)

В последней формуле обозначает отклонение от границы. Допуская возможность отклонения, мы одновременно вводим штрафные санкции за него = С . Тогда задача превращается в многокритериальную – увеличение полосы увеличивает надежность классификации и одновременно суммарную ошибку . Можно переформулировать в духе свертки критериев таким образом:

Найти w, доставляющие

при

(4.5.17)

Выбор величины С можно рассматривать как указание относительной значимости ширины разделяющей полосы и ошибки.

Введем множители Лагранжа и составим функцию Лагранжа задачи (4.5.17).

(4.5.18)

Оптимальное решение достигается в седловой точке функции Лагранжа. Необходимые условия минимума по переменным w и b запишем в виде:

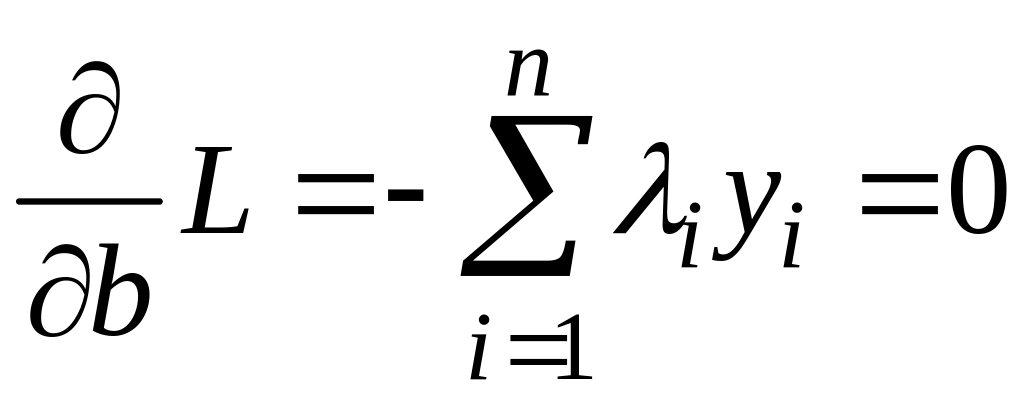
Подставляем в (4.5.18) получаем

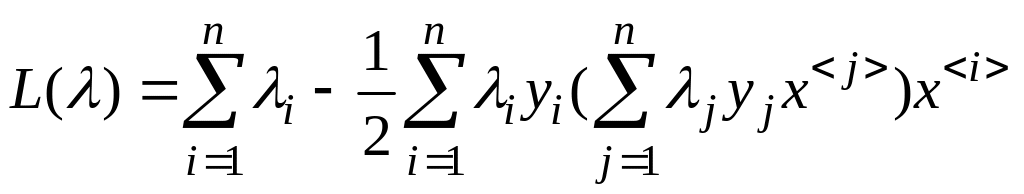
Задача поиска седловой точки теперь переформулируем

(4.5.19)

при ограничениях и (4.5.19')

Решение этой задачи имеет вид:

(4.5.20) для произвольного s с .

Классифицирующая функция имеет вид .

В программной реализации метода задачу построения линейного классификатора целесообразно ставить сразу в постановке (4.5.17), так как заранее неизвестно разделимы ли классы в обучающей выборке. Если заранее известно, что классы в обучающей выборке линейно разделимы, можно свести задачу к задаче (4.5.7), задав большой штраф за отклонение.

Мы рассмотрели случай линейно разделимых классов и линейно разделимых с погрешностью классов. Рассмотрим нелинейный вариант SVM. Как разделить классы, представленные на рис. 4.5.4

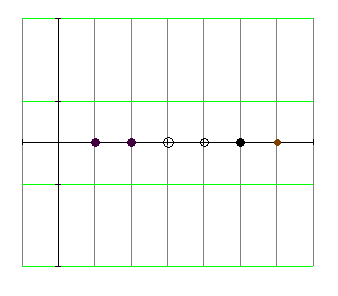
Рис .4.5.4 Один класс внутри другого на прямой линии.

Отображение на плоскость делает точки отделимыми в этой плоскости.

Рис. 4.5.5. Отображение в признаковое пространство большей размерности.

В этом и состоит идея нелинейного SVM.

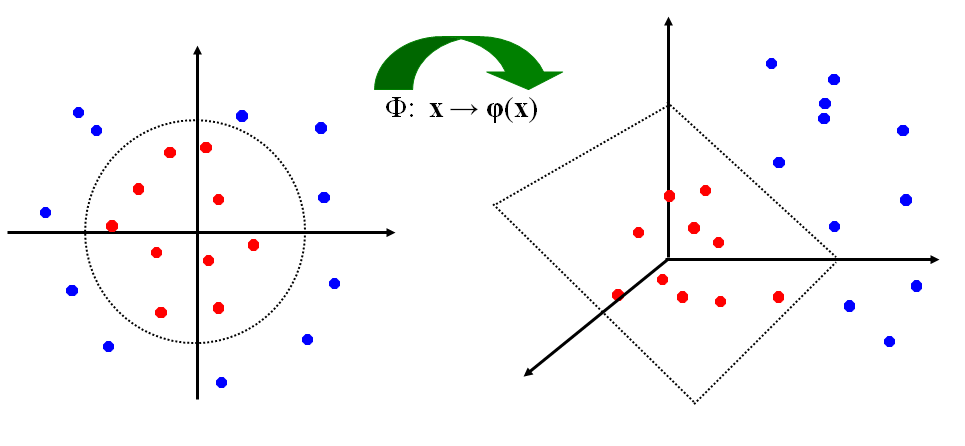
Рис.4.5.6. В пространстве большей размерности точки линейно отделимы.

В новом пространстве задача формулируется так:

(4.5.21)

при ограничениях и (4.5.21’)

Решение этой задачи имеет вид:

(4.5.22)

для произвольного s с .

Классифицирующая функция имеет вид :

. (4.5.23)

Поскольку для построения классифицирующей функции достаточно иметь только скалярные произведения отображений, то появилась идея вычислять матрицу

в обход построения отображений φ. получила название функции ядра (kernel function).

Например, вычисление с функции ядра соответствует отображению

где

. (4.5.24)

Выбор функции ядра приводит к поиску разделяющей гиперплоскости в пространстве большей размерности:

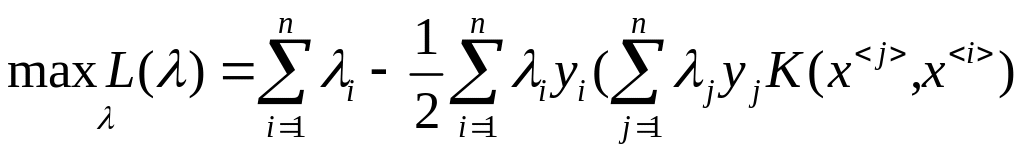(4.5.25)

при ограничениях и (4.5.25')

Для вычисления b можно использовать формулу

(4.5.26)

С учетом формула (22) для b получит вид:

(4.5.26’) 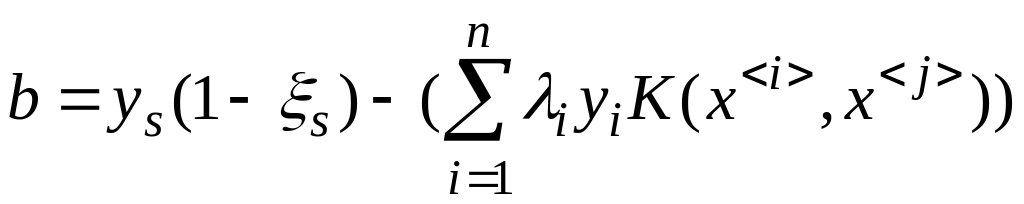(4.5.26”)

Таким образом, зная только функцию ядра, можно в обход (x) рассчитать параметр b. Классифицирующую функцию можно записать, не используя w.

2. Теорема Байеса и вероятностные рассуждения.

Основой для вероятностных рассуждений является байесовский вывод и теорема Байеса Байесовский вывод — статистический вывод, в основе которого лежит пересчет вероятностей на основании некоторого свидетельства (наблюдения, факта, информации); Этот пересчет производится по формуле (теореме) Байеса [2].

Теорема Байеса задает переход от исходной априорной вероятности предположения (гипотезы) к обновленной оценке, получаемой на основании данных нового свидетельства, следующим образом:

где

H-представляет конкретную гипотезу;

P(H)-называется априорной вероятностью гипотезы H, которая была введена прежде, чем новое свидетельство E стало доступным;

P(E|H)--называется условной вероятностью наблюдения свидетельства , если гипотеза верна; её также называют правдоподобием (likelyhood), когда она рассматривается как функция - для фиксированного ;

P(E)-называется полной (смешанной , маргинальной) вероятностью E: вероятность наблюдения нового свидетельства E согласно всем возможным гипотезам; может быть вычислено по формуле:

как сумма произведений всех вероятностей любого полного набора взаимно исключающих гипотез и соответствующих условных вероятностей.

называется апостериорной вероятностью гипотезы H для данного E.

Для иллюстрации предположим, что есть две коробки. В 1-ой коробке 10 белых жетонов и 30 черных, в то время как во 2-ой коробке по 20 жетонов каждого цвета. Подсчитаем вероятность извлечь белый жетон из наугад выбранной коробки.

Пусть — гипотеза, что жетон из первой коробки, а — гипотеза, что из второй. В силу неразличимости коробок в данном конкретном случае вероятности гипотезе одинаковы , а так вместе они должны составить 1, то обе равны 0.5. Событие E— факт (свидетельство, наблюдаемое событие) – вытянут жетон белого цвета.

Из содержания коробок можно оценить, что

и .

Расчет по формуле полной вероятности в предположении, что выбор коробок равновероятен, даёт .

После того как вытянут жетон, и он оказался белого цвета, кажется более вероятным, что он взят из коробки, в которой больше белых жетонов. Теорема Байеса позволяет дать численный расчет.

Формула Бейеса тогда даёт

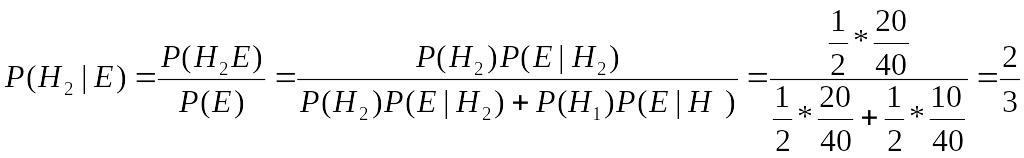
Байесовский вывод лежит в основе работы Байесовских сетей влияния. Байесовская сеть - это граф без циклов, вершины которого представляют переменные, а ребра выражают зависимости между переменными [13,20].

Рассмотрим простейшую Байесовскую сеть, состоящую из двух переменных, соответствующих задаче о двух коробках, представленной выше.

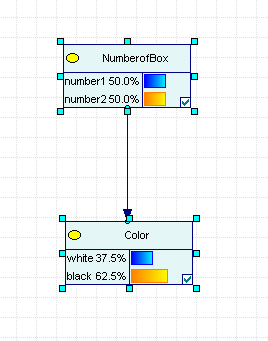
Рис.2.1.1 Задача и коробках.

На рисунке 2.1.1 узлы сети представлены прямоугольниками. На верхнем узле представлены априорные гипотезы выбора коробки.

=0.5.

Связующая стрелка - отражает влияние первого узла на второй.

Данное влияние отражается в условных вероятностях, представленных на рис.2.1.2.

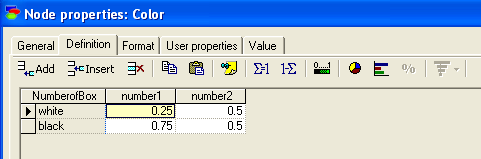
Рис.2.1.2. Условные вероятности извлечь шар из коробок

На узле «следствия» щелчком мыши можно имитировать выбор цвета шара. На узде «причин» мы наблюдаем результат пересчета вероятностей гипотез.

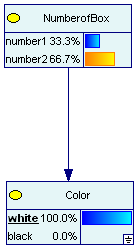
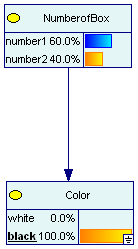
Рис.2.1.3. Апостериорные вероятности коробок.

На верхнем узле «причин» отразился пересчет исходных вероятностей в апостериорные, результат извлечения жетона, определенного цвета.

Рассмотрим еще одно вероятностное рассуждение, представленное с помощью Байесовской сети (рис. 2.1.4).

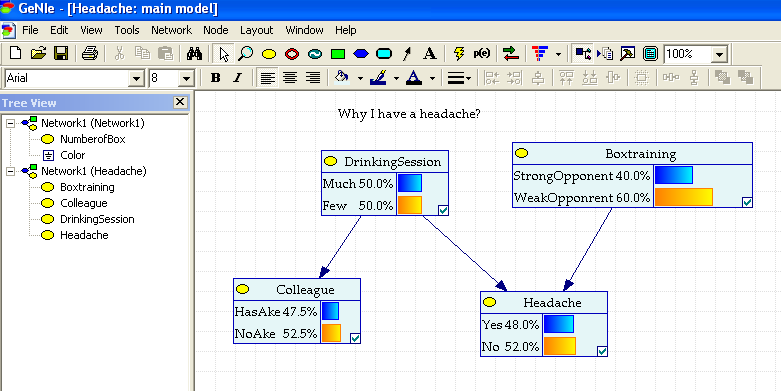
Рис.2.1.4. Задача о причине утренней головной боли(Headache).

Случайная величина (Headache) представлена нижним правым узлом на рис.2.1.4. Рассматриваются две причины, которые могли вызвать головную боль -

вчерашняя тренировка по боксу (Boxtraining)), либо последовавший за ней банкет(DrinkingSession). Условные вероятности влияния названных факторов отражены в таблице условных вероятностей узла (Headache).

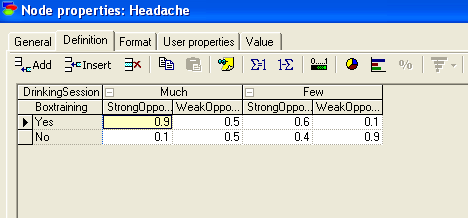
Рис. 2.1.5. Условные вероятности (Headache).

(Мы воспользовались свободно распространяемой системой GINIE 2.0 для демонстрации задачи. В этой системе имеется ограничение на идентификаторы переменных – допустимы только латинские символы).

Априорные вероятности гипотез о причинах головной боли видны на соответствующих узлах сети.

На узле Headache даны маргинальные вероятности возможных состояний. При таком образе жизни почти в половине случаев голова будет болеть.

Тот факт, что голова болит, заставляет пересчитать априорные вероятности причин.

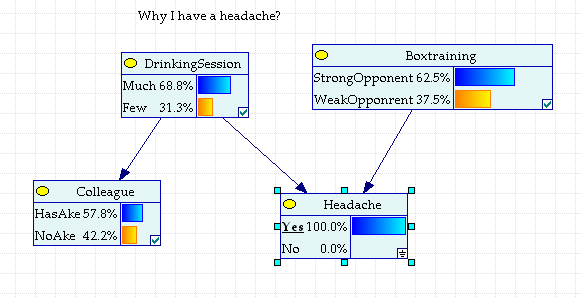
Рис.2.1.6. Апостериорные вероятности причин головной боли.

Для исключения одной из гипотез можно связаться с коллегой, участвовавшим в банкете, и уточнить болит ли у него голова.

Если у коллеги голова болит, а боксировать ему, как видно из условий задачи не пришлось, то вывод однозначно в «пользу» DrinkingSession.

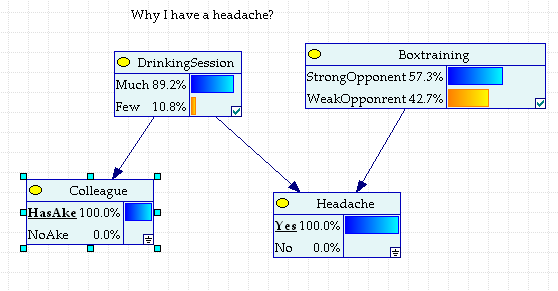
Рис. 2.1.7. Голова болит и у коллеги, участвовавшем в банкете

Если же у коллеги голова здоровая, то новые оценки апостериорных вероятностей будут следующими:

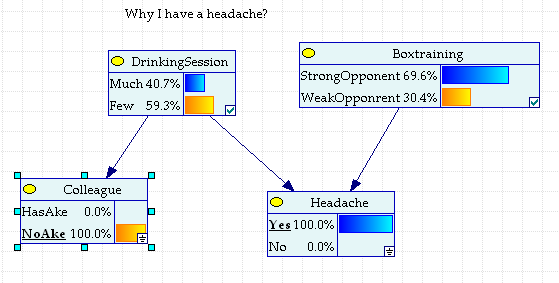
Рис.2.1.8 У коллеги голова не болит

Рис.2.1.8 не уменьшая значения вреда алкоголя, все-таки заставляет предполагать, что противник на тренировке был значительно успешнее.

Эксперименты с сетью можно продолжать. Одно полезное упражнение. Заметьте, что если не задано свидетельство конкретное о головной боли, то свидетельство о том, болит или не болит голова у коллеги, не проникает в узел (Boxtraining). При заданном свидетельстве о Headache , оно меняет оценки гипотез. Если свидетельство в пользу DrinkingSesion, то исключается Boxtraining, и наоборот.

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 12

1. Модель классификатора с использованием «машины опорных векторов». Линейно неразделимые множества

Пусть имеется набор учебных примеров, каждый из которых имеет два числовых параметра и отнесенных к одному из классов y = {-1,1}:

x1	x2	y
0	1	1
1	2	1
2	0	1
3	3	-1
3	4	-1
5	4	-1

Таблица 4.5.1. Учебные примеры для классификатора

На рис.4.5.1 классы отображены цветом так, что класс 1 закрашен белым цветом, а класс -1 –черным.

На рис. 4.5.2 показаны несколько прямых разделяющих классы.

Рис.4.5.1 Пример обучающей выборки из таблицы 4.5.1

Рис. 4.5.2 Прямые, разделяющие классы

Рис. 4.5.3. Опорные векторы.

Одной из разделяющих линий соответствует разделяющая полоска наибольшей ширины. Точки, касающиеся полоски разделения и обведенные кружочками, – «опорные вектора»

Согласно известному факту из аналитической геометрии расстояние от точки на плоскости до прямой, заданной уравнением , выражается формулой

(4.5.1)

Расстояние имеет знак, причем точки, расположенные по разные стороны прямой, имеют разные знаки. Выбор знака зависит от знака коэффициентов уравнения прямой, и если поменять знак, то точки на плоскости, имевшие знак плюс, получат знак минус и наоборот.

Обозначим ширину разделяющей полоски на рисунке 4.5.3 буквой ρ. Для расстояний от прямой до точек «светлого класса» выполняется неравенство (чем дальше, тем расстояние больше, так как оно выбрано положительным):

(4.5.2)

Для точек «черного» класса выполняется неравенство (чем дальше, тем расстояние меньше, так как оно выбрано отрицательного знака):

(4.5.3)

Эти два неравенства можно объединить в одно, учитывая знак, используемый для обозначения класса (умножение на -1 изменяет знак неравенства)

(4.5.4)

поскольку мы принимаем, что

для чёрных точек, и (4.5.5)

для белых точек. (4.5.5’)

На основании данной обучающей выборки должен быть построен классификатор, который будет определять класс точек по их координатам, Доказано, и это интуитивно ясно, что чем шире разделяющая полоса (то есть, чем больше ρ), тем меньше риск допустить ошибку в случае, если координаты «новой точки» задаются с погрешностью.

Это соображение приводит к задаче оптимизации с учетом ограничений:

при

(4.5.6)

Здесь n – общее число точек (примеров в обучающей выборке).

В силу того, что мы можем по желанию выбирать нормирующий множитель в (4.5.2), установим его равным

(4.5.6’)

Тогда задача (4.5.6) формулируется в виде:

при

(4.5.7)

Используя множители Лагранжа , получим функцию Лагранжа задачи оптимизации (4.5.7).

(4.5.8)

Принято множители Лагранжа считать положительными и выбирать знак минус перед суммой с ограничениями. Доказывается в теории выпуклого программирования, что решению задачи соответствует седловая точка функции Лагранжа, доставляющая минимум по параметрам прямой и максимум по множителям Лагранжа.

Необходимые условия минимума L:

(4.5.9)

Первые уравнения из (4.5.9) подставляем в Лагранжиан (4.5.8) и получим с учетом последнего

(4.5.10)

Получилась так называемая дуальная форма Лагранжиана, который зависит теперь только от множителей. Ей соответствует задача оптимизации:

(4.5.11)

при ограничениях и (4.5.12)

Полученная задача является задача квадратичной оптимизации при линейных ограничениях. Существуют эффективные программные средства для её решения. Например, в MathCad решение может быть получено с помощью простой записи:

Далее полученные множители подставляем в (4.5.9) , чтобы получить w, b и из них (4.5.6’).

(4.5.13)

Свободный член уравнения прямой определим из условия, что расстояния от опорных точек (для которых множитель Лагранжа не равен нулю) до искомой прямой должны быть равны и противоположны по знаку.

Для опорного вектора s соотношение (4.5.7) выполняется как точное равенство.

Последнее равенство можно записать, используя (4.5.13)

Если умножить обе части последнего равенства на , то получаем

, откуда

для произвольного опорного вектора s.

При программировании вычислений удобно брать не произвольный вектор, а среднее по опорным векторам.

(4.5.14)

На MathCad это может быть выполнено с помощью записи (предварительно приводим уравнение прямой к нормальной форме, тогда подстановка координат точек сразу даст расстояние):

_{Окончательно, ширина полосы разделения}

Классифицирующая функция может быть теперь записана в виде функции, определяющий знак полуплоскости в которой окажется классифицируемый объект:

(4.5.15)

Здесь суммирование производится по опорным векторам, для которых λ больше нуля.

Пусть теперь в обучающей выборке точки не разделены.

Рис. 4.5.4 Пример обучающего множества с линейно неразделяемыми классами.

Вместо «жёстких» условий разделения классов

принимаем «смягчение» границ:

и объединяем их в одно

(4.5.16)

В последней формуле обозначает отклонение от границы. Допуская возможность отклонения, мы одновременно вводим штрафные санкции за него = С . Тогда задача превращается в многокритериальную – увеличение полосы увеличивает надежность классификации и одновременно суммарную ошибку . Можно переформулировать в духе свертки критериев таким образом:

Найти w, доставляющие

при

(4.5.17)

Выбор величины С можно рассматривать как указание относительной значимости ширины разделяющей полосы и ошибки.

Введем множители Лагранжа и составим функцию Лагранжа задачи (4.5.17).

(4.5.18)

Оптимальное решение достигается в седловой точке функции Лагранжа. Необходимые условия минимума по переменным w и b запишем в виде:

Подставляем в (4.5.18) получаем

Задача поиска седловой точки теперь переформулируем

(4.5.19)

при ограничениях и (4.5.19')

Решение этой задачи имеет вид:

(4.5.20) для произвольного s с .

Классифицирующая функция имеет вид .

В программной реализации метода задачу построения линейного классификатора целесообразно ставить сразу в постановке (4.5.17), так как заранее неизвестно разделимы ли классы в обучающей выборке. Если заранее известно, что классы в обучающей выборке линейно разделимы, можно свести задачу к задаче (4.5.7), задав большой штраф за отклонение.

Мы рассмотрели случай линейно разделимых классов и линейно разделимых с погрешностью классов. Рассмотрим нелинейный вариант SVM. Как разделить классы, представленные на рис. 4.5.4

Рис .4.5.4 Один класс внутри другого на прямой линии.

Отображение на плоскость делает точки отделимыми в этой плоскости.

Рис. 4.5.5. Отображение в признаковое пространство большей размерности.

В этом и состоит идея нелинейного SVM.

Рис.4.5.6. В пространстве большей размерности точки линейно отделимы.

В новом пространстве задача формулируется так:

(4.5.21)

при ограничениях и (4.5.21’)

Решение этой задачи имеет вид:

(4.5.22)

для произвольного s с .

Классифицирующая функция имеет вид :

. (4.5.23)

Поскольку для построения классифицирующей функции достаточно иметь только скалярные произведения отображений, то появилась идея вычислять матрицу

в обход построения отображений φ. получила название функции ядра (kernel function).

Например, вычисление с функции ядра соответствует отображению

где

. (4.5.24)

Выбор функции ядра приводит к поиску разделяющей гиперплоскости в пространстве большей размерности:

(4.5.25)

при ограничениях и (4.5.25')

Для вычисления b можно использовать формулу

(4.5.26)

С учетом формула (22) для b получит вид:

(4.5.26’) (4.5.26”)

Таким образом, зная только функцию ядра, можно в обход (x) рассчитать параметр b. Классифицирующую функцию можно записать, не используя w.

(4.5.27)

2. Расчет среднего числа загруженных каналов очереди в СМО открытого типа

Зная вероятности состояний системы массового обслуживания в установившемся режиме, можно вычислить названные ранее характеристики ее работы.

Вероятность отказа равна вероятности того, что система находится в состоянии n+m и, следовательно, равна .

Вероятность принятия заявки на обслуживание равна

Число заявок, поступающих в единицу времени (интенсивность потока) равно λ. Из их числа доля P_yes обслуживается в системе, и, таким образом, производительность системы равна

Эту производительность обеспечивают каналы, каждый из которых в среднем в единицу времени обслуживает μ заявок. Значит в среднем занято A/ μ каналов.

Подсчитаем среднее число заявок в очереди Lq.

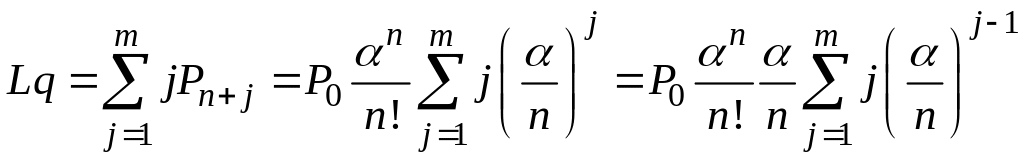Получилась легко программируемая формула. Можно было бы продолжить аналитические выкладки, заметив, что под знаком суммы стоит производная от .

Найдем выражение для среднего времени пребывания заявок в очереди. Если очередная заявка застаёт очередь пустой и имеется хотя бы один свободный канал, то она не ждет вовсе. Если при свободной очереди каналы заняты, то в среднем заявка ждет .Если заявка застает k-1 заявку ( становится в очередь k-ой), то в среднем она должна переждать всех своих предшественниц плюс своё . Таким образом, среднее время равно . Наконец, если заявка застает в очереди m заявок, то она опять же не ждёт, а уходит необслуженная. Значит, среднее время можно подсчитать по формуле

(3.2.12)

Вспоминая, что выполняется рекуррентное соотношение ,

Используя его в формуле (3.2.12), получим

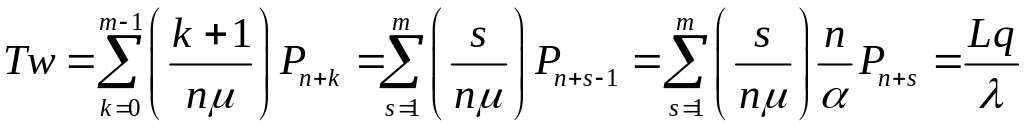(3.2.13)

Полученная формула известна как формула Литтла

В заключение приводим формулу для времени пребывания заявки в системе обслуживания. Если заявка принималась на обслуживание, то среднее время обслуживания равно , а если получила отказ, то ее время пребывания в системе равно нулю. Среднее время равно времени . К этому времени надо прибавить среднее, проведенное в очереди Tw. В итоге для среднего времени, проведенного в системе, имеем

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 11

1. Выявление зависимости по методу опорных векторов. Линейная и нелинейная регрессия.