Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный университет управления

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

матмод.doc

Скачиваний:

Добавлен:

20.09.2019

Размер:

3.52 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 1

Моделирование процесса установления. Логистическая кривая.

ЛОГИСТИЧЕСКАЯ КРИВАЯ роста популяций, построенная на арифметич. шкале S-образная кривая, отражающая неуклонный рост численности какой-либо популяции от исходного положения до верхнего предела увеличения численности (верхняя асимптота), после чего колеблется параллельно абсциссе (оси времени). Описывает реальный тип роста естественных популяций всех видов живых организмов. Математический анализ логистической кривой впервые произведен П. Ферхульстом (1838) с помощью логистического уравнения. Уравнение ферхульста-пирла лежит в основе всех математических моделей конкуренции,хищничества, симбиоза (паразитизма). Исходные предположения для вывода уравнения при рассмотрении популяционной динамики выглядят следующим образом:

скорость размножения популяции пропорциональна её текущей численности, при прочих равных условиях

скорость размножения популяции пропорциональна количеству доступных ресурсов, при прочих равных условиях. Таким образом, второй член уравнения отражает конкуренцию за ресурсы, которая ограничивает рост популяции.

математическое моделирование, т.е. процесс установления соответствия реальному объекту некоторого набора математических символов и выражений. Математические модели наиболее удобны для исследования и количественного анализа, позволяют не только получить решение для конкретного случая, но и определить влияние параметров системы на результат решения; Сущность оптимизации (улучшения) моделей состоит в их упрощении при заданном уровне адекватности. В основе оптимизации лежит возможность преобразования моделей из одной формы в другую. Основными показателями, по которым возможна оптимизация модели, являются время и затраты средств для проведения исследований и принятия решений с помощью модели.

2. Численный метод решения обыкновенного дифференциального уравнения первого порядка (метод Эйлера с коррекцией) Рассмотрим дифференциальное уравнение

(1)с начальным условием Подставив в уравнение (1), получим значение производной в точке : При малом имеет место:

Обозначив , перепишем последнее равенство в виде: (2)

Принимая теперь за новую исходную точку, точно также получим: В общем случае будем иметь: (3)Это и есть метод Эйлера. Величина называется шагом интегрирования. Пользуясь этим методом, мы получаем приближенные значения у , так как производная на самом деле не остается постоянной на промежутке длиной . Поэтому мы получаем ошибку в определении значения функции у , тем большую, чем больше . Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. Его недостатки – малая точность и систематическое накопление ошибок. Более точным является модифицированный метод Эйлера или метод Эйлера с пересчетом. Его суть в том, что сначала по формуле (3) находят так называемое «грубое приближение»: а затем пересчетом получают тоже приближенное, но более точное значение: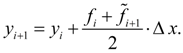

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 2

Моделирование процесса распространения инноваций (уравнения Басса). Аналитическое и численное решение.

Модель распространения является одним из инструментов для описания, и иногда предсказания, числа покупок новых товаров длительного пользования. Уравнение Басса задает изменение численностей адептов новшества и основывается на гипотезе, что скорость изменения численности определяется количеством потенциальных потребителей новшества по формуле:

(1.2.1)

В этом уравнении

M – общее число возможных потребителей новшества;

Y – численность потребителей, уже приобщившихся к новшеству;

M -Y – количество тех, которым еще предстоит приобщиться;

p – коэффициент, который показывает вероятность того, что те, кто входит число (M-Y) еще не испытавших счастья, сами откликнуться на воздействие новшества (через рекламу, например);

q – коэффициент, учитывающий воздействие новшества на неохваченных благодаря их контактам с теми, кто уже был охвачен .

Выделяется две категории потребителей – новаторы и подражатели.

В уравнении (1.2.1), таким образом, можно разглядеть два характерных процесса - роста и гибели особей в популяции и, следовательно, ожидать, что процесс приведет к кривой установления аналогичной логистической кривой.

Очевидно, что начальное значение численности адептов новшеств равно нулю, то есть Y(0) = 0 .

Уравнение (1.2.1) относится к виду дифференциальных уравнений с разделяющимися переменными:

(1.2.2)

Разложим на простые дроби

(1.2.3)

что дает

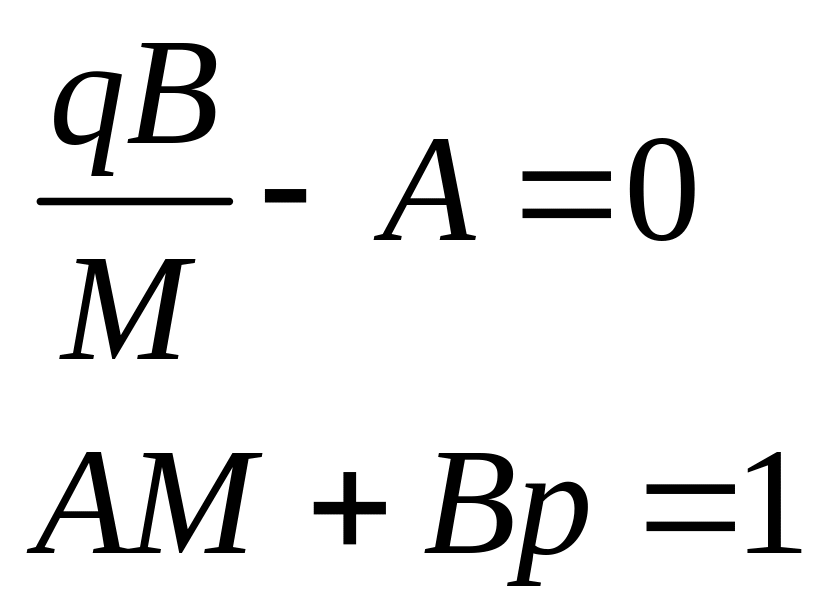(1.2.4)

Получаем

(1.2.5)

Уравнение (1.2.2) приобретает тогда вид:

(1.2.6)

Интегрирование даёт

(1.2.7)

и, избавляясь от логарифмов, получаем

(1.2.8)

Использовав начальное условие , определим значение С:

(1.2.9)

и, после подстановки в (1.2.8)

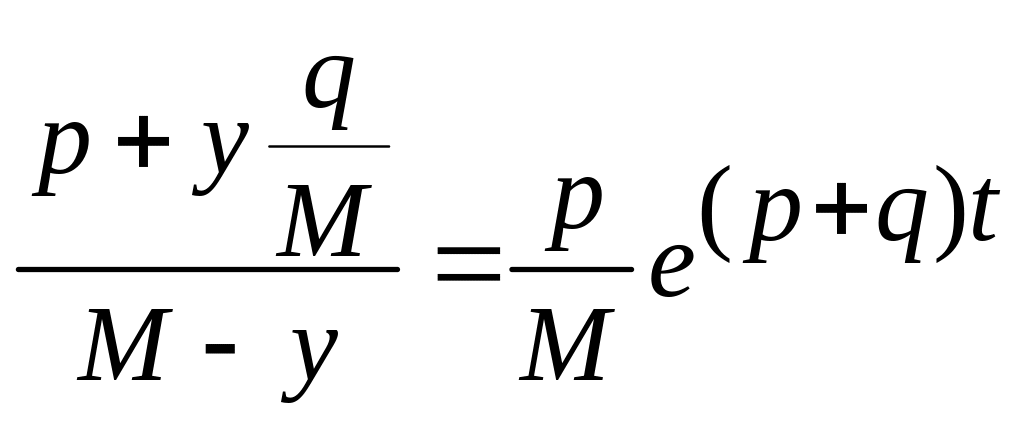(1.2.10)

Остается выразить явно y.

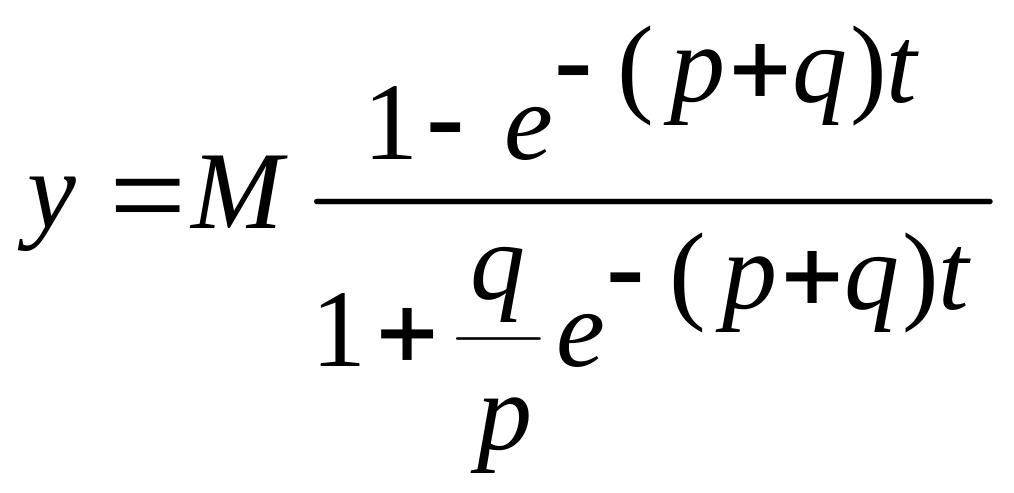(1.2.11)

Решение в графическом виде и численное решение уравнения получено с помощью следующей программы MathCad.

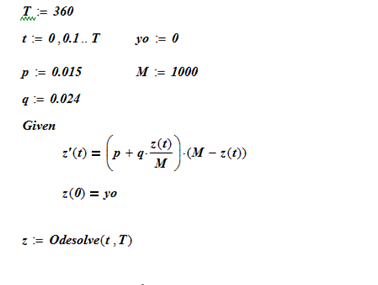
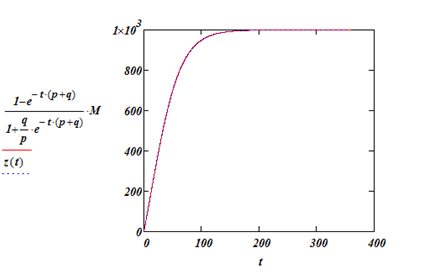
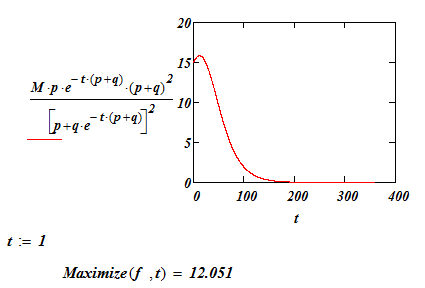
Определим точку максимальных продаж

(1.2.12)

Вычисление максимальной скорости распространения новшества можно провести , в среде MathCad, используя команду Maximize(f,t).

Рассмотрим видоизменение модели с учетом повторных покупок. Пусть срок жизни товара равен d, после которого обладатель новшества переходит в категорию потенциальных клиентов. В правой части (1.2.1) множитель определяет численность этой категории потенциальных клиентов. Для учета повторных покупок нужно брать значение этой численности до приобретения товара, то есть брать . Получаем уравнение

(1.2.13)

Численное интегрирование в среде MathCad иллюстрируется программой на следующей страницк.:

Результат вычисления представлен на графике (рис . 1.2.1).

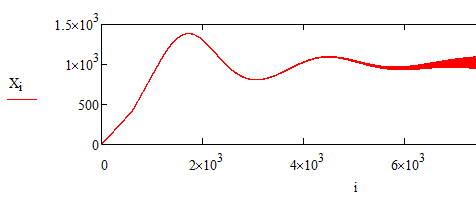
Рис. 1.2.1 График распространения инноваций с учетом повторных покупок.

Построение модели в форме правил в задаче исследования ассоциативных связей.

Ассоциативная связь - вид связи, устанавливаемый исходя из заданного сочетания признаков данных, которые образуют упорядоченные последовательные цепочки. Указатели на связанные данные могут размещаться в самих данных или программных средствах управления базой данных.

Ряд работ, рассматривал возможности понятия ассоциативной памяти в применении к языкам программирования и аппаратной реализации процессора. И в качестве рабочего определения пользовались следующим:

Под ассоциативной памятью обычно понимается некоторый набор, или совокупность элементов, обладающих способностью хранить информацию. Доступ к этим элементам осуществляется одновременно и параллельно в соответствии с содержанием хранящихся в них данных, а не путем задания адреса или расположения элемента.

Но такое понимание ассоциативной памяти отражает, в сущности, лишь факт наличия взаимосвязей между данными и не имеет отношения к самому механизму хранения информации. Поэтому для обозначения такого механизма хранения информации используется термин «память с адресацией по содержанию» (ПАС).

Как только акцент был сделан на устройство «памяти с адресацией по содержанию», то стало возможным упростить требования к самому пониманию ассоциативности, и разработать устройства лишь в некотором смысле обладающие ассоциативностью. Так, например, первое, что было упрощено — это предположение, что параллелизм при выполнении операций поиска по существу не является принципиальной функциональной характеристикой.

Второе упрощение связано с отрицанием необходимости распределенной памяти, так как ассоциативности в смысле памяти, с адресацией по содержанию, формально можно добиться и без необходимости распределять между элементами памяти информацию. В противовес этому можно хранить единицу информации целостно в определенной ячейке, имея лишь информацию о непосредственных связях данной ячейки с другими — таким образом, мы приходим к пониманию семантических сетей. Данные принципы также используются при индексировании и поиске в современных базах данных. Конечно, в этом смыле это упрощение противоречит идеям коннективизма (которые базируются на искусственных нейронных сетех), и плавно перетекает к идеям символизма.

Главное, что теряется при таком упрощении — это одно из удивительных свойств биологической памяти. Известно, что разного рода повреждения ткани мозга приводят к нарушениям функциональных характеристик памяти. Тем не менее оказалось исключительно трудно выделить в работе отдельных нейронных структур явления, связанные с локализацией функций памяти. Объяснение этого базируется на предположении, что в мозгу следы памяти представлены в виде пространственно распределенных структур, формируемых в результате некоторого преобразования первичных восприятий.

Но тем не менее, хоть при таком упрощении были потеряны ряд биологически правдоподобных свойств, что важно при моделировании мозга, но зато в техническом смысле стало понятно как реализовать память, адресуемую по содержанию. Благодаря этому появились идеи о хешировании, которые затем были реализованы как в языках программирования, так и при аппаратной реализации некоторых процессоров.

Третье упрощение связанно с точностью совпадения искомой информации. Выборка данных на основе их содержания всегда предполагает ту или иную форму сравнения задаваемого извне ключа, по которому должен осуществляться поиск, с некоторой частью или со всей информацией, которая хранится в ячейках памяти. Целью сравнения не всегда должно быть появление информации, совпадающей с ключевой. Например, при отыскании значений, которые расположены внутри заданного интервала. В этом случае мы имеем классический способ использования SQL при отборе из базы данных. Но возможен вариант поиска, при котором необходимо среди совокупности данных найти те, которые наилучшем образом (в смысле некоторой заданной меры) соответствуют ключевой информации.

В такой постановке задача ассоциативной выборки весьма близка к задаче распознавания образов. Но определяющим является методы, которые при этом используются — если смысл ассоциативности не подвержен описанным здесь упрощениям, то мы имеем дело с распознаванием образов с помощью искусственных нейронных сетей, в противном случае мы имеем дело с оптимизацией работы баз данных (а также аппаратных кэшей процессоров), или способами ассоциативного представления данных (например, семантических сетей). Отсюда должно быть понятно, что ассоциативное представление данных, и некоторые приемы работы с памятью, адресуемой по содержанию недостаточны для пониманием под этим ассоциативной памяти в полном смысле слова.

Четвертое упрощение может быть связанно с так называемой проблемой временных ассоциаций, что с точки зрения программирования относится к теории автоматов. Эти проблемы связаны с разработкой методов запоминания и извлечения из памяти упорядоченных во времени последовательностей. При этом они могут разветвляться, образуя вторичные альтернативные последовательности, причем переход к одной из них определяется содержанием некоторой фоновой, или контекстной информации. Указанные последовательности могут также содержать замкнутые циклы.

Таким образом, с точки зрения программирования или символизма, по отношению к ассоциативной памяти имеются все те же проблемы и задачи, как и в искусственном интеллекте. Различием является то, что в программировании могут быть сделаны упрощения и построены методы, которые лишь частично удовлетворяют пониманию ассоциативной памяти. В то время как коннективизм пытается решить проблему ассоциативной памяти, используя методы которые не содержат упрощений в описанных здесь смыслах, обладают некоторой стохастичностью и непредсказуемостью в смысле работы метода, но в конечном счете дающих осмысленный результат в областях распознавания образов или адаптационного управления.

Перцептрон состоит из трёх типов элементов, а именно: поступающие от сенсоров сигналы передаются ассоциативным элементам, а затем реагирующим элементам. Таким образом, перцептроны позволяют создать набор «ассоциаций» между входными стимулами и необходимой реакцией на выходе. В биологическом плане это соответствует преобразованию, например, зрительной информации в физиологический ответ от двигательных нейронов. Согласно современной терминологии, перцептроны могут быть классифицированы как искусственные нейронные сети:

с одним скрытым слоем;[nb 3]

с пороговой передаточной функцией;

с прямым распространением сигнала.

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 3

Составление дифференциального уравнения погони. Численное решение при заданном виде кривой для преследуемого объекта.

Задача состоит в определении траектории, по которой движется догоняющий (хищник, пиратское судно, полицейский и т.п.), если преследуемый (жертва, торговое судно, нарушитель и пр.) движется по заданной кривой, причем направление движения догоняющего всегда направлено на преследуемого [4].

Пусть – точка на кривой, соответствующей траектории догоняющего, а –точка на траектории преследуемого, последняя пусть задана уравнениями

По условию задачи скорость догоняющего направлена вдоль вектора

, что можно записать формулой:

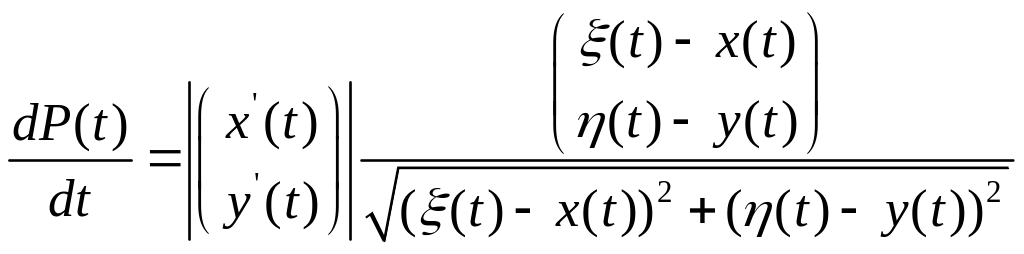1.4.1

Величина скорости догоняющего по условию задачи равна

(1.4.2)

Следовательно

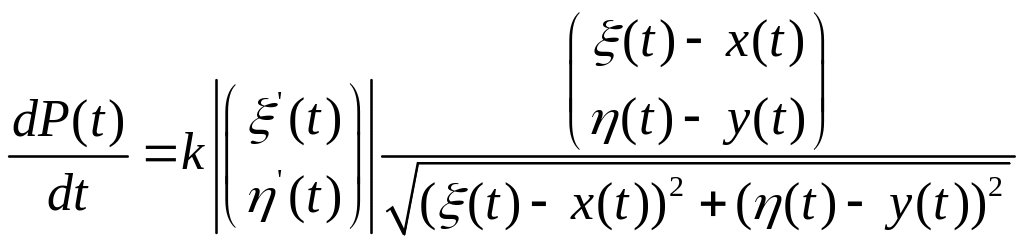(1.4.3)

Если скорость преследуемого постоянна по величине, то из последнего соотношения имеем:

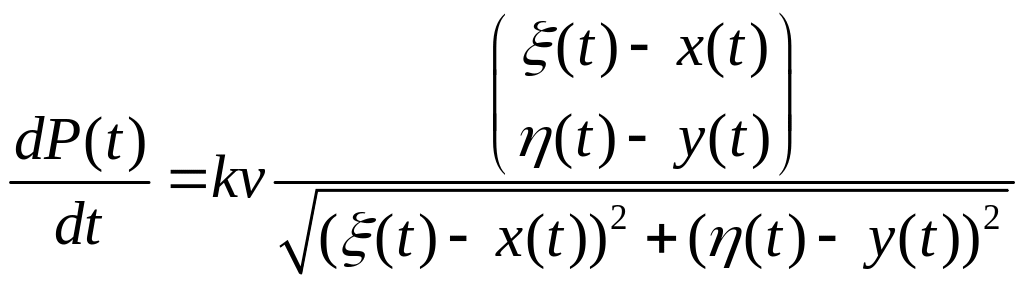1.4.4

В результате модель погони выражается системой дифференциальных уравнений:

1.4.5

1.4.5’

Пусть преследуемый движется по прямой параллельной оси oY.

Тогда и .

Догоняющий в начальный момент времени находится в начале системы координат. Решение системы уравнений (1.4.5) в MathCad

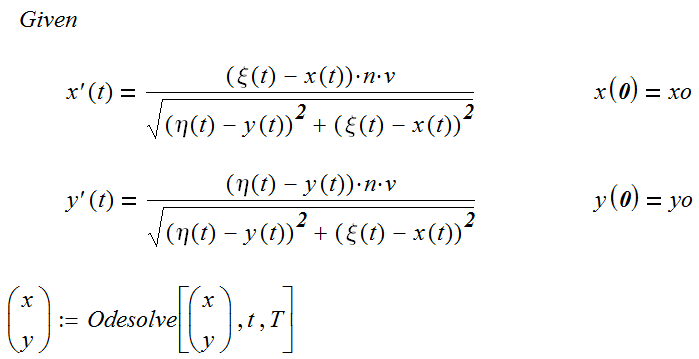
В графической форме решение представлено на рис

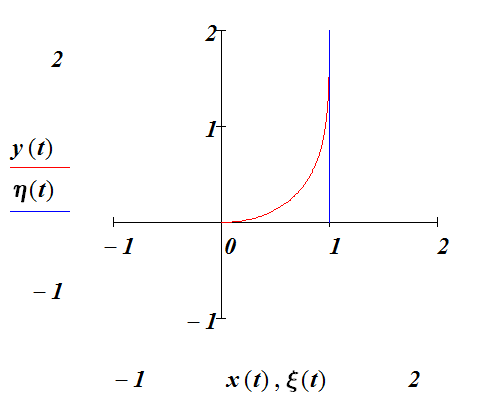
Рис. 1.4.1. Решение уравнения погони при и .

Пусть преследуемый движется по прямой, заданной уравнениями

и с постоянной скоростью v. Результат представлен на рис 1.4.2.

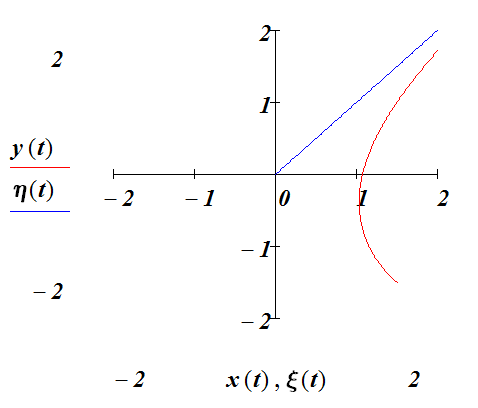
Рис. 1.4.2 Решение уравнения погони при и .

Пусть преследуемый движется по окружности, заданной уравнениями.

и с постоянной скоростью v. Следующий рисунок показывает результат.

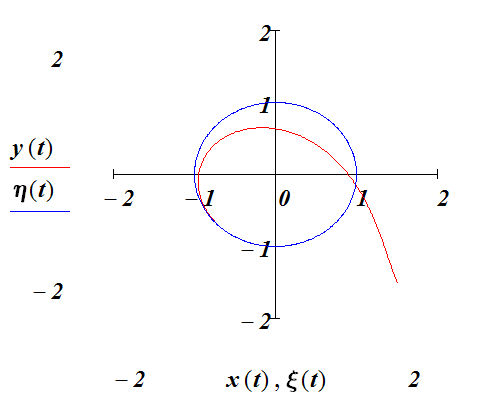
Рис. 1.4.3 . Решение уравнения погони при и .

Пусть преследуемый движется по прямой, совпадающей с осью Ox и заданной уравнениям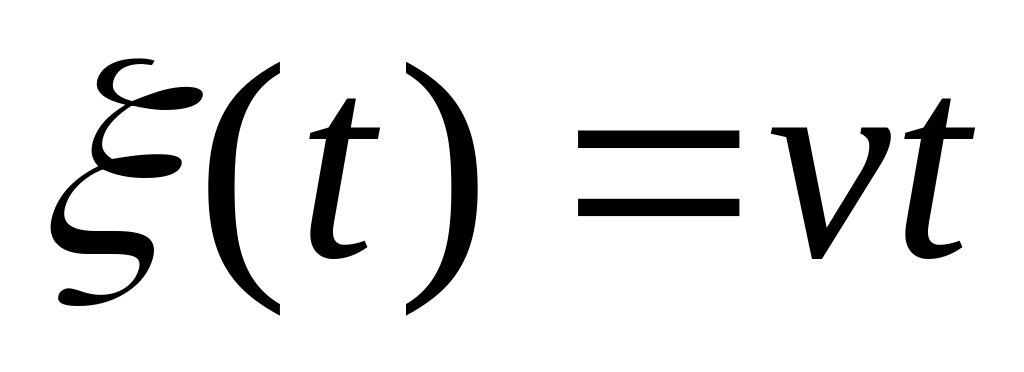и и . Тогда результат изображен на рис 1.4.4.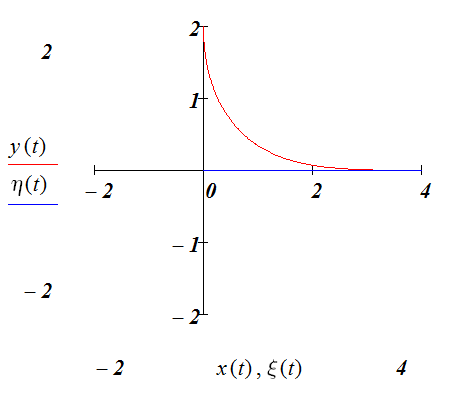

Рис. 1.4.4. . Решение уравнения погони при и .

Мы привели четыре примера построения кривой погони с помощью численного решения системы дифференциальных уравнений (1.4.5).

Для условий первого примеры приводим аналитический вывод формулы кривой погони.

По условию задачи тангенс наклона касательной к кривой догоняющего

(1.4.6)

И для условий первого примера

(1.4.7)

Пока преследуемый проходит путь vt догоняющий проходит путь

(1.4.8)

Приняв во внимание, что из (1.4.7) получаем

(1.4.9)

Дифференцирование по x даёт

(1.4.10)

И, наконец

Обозначим p = . Тогда уравнение (1.4.10) можно переписать в виде

(1.4.11)

Интегрирование (1.4.11) дает

(1.4.12)

Или, что то же

, (1.4.13)

Здесь C – произвольная постоянная.

Избавляемся от логарифмов и получаем

(1.4.14)

Решение относительно p дает

(1.4.15)

Следующим шагом является решение дифференциального уравнения

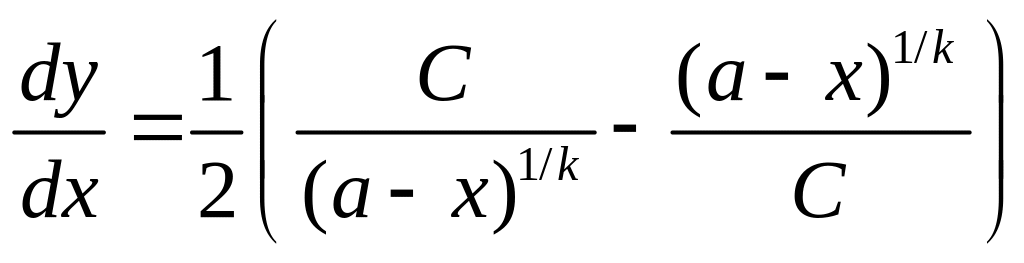(1.4.16)

Интегрирование дает для y(x) выражение

(1.4.17)

где c’ – произвольная постоянная (вторая) и k ≠1.

Пусть догоняющий начинает движение в начале координат (выбор системы координат) и его скорость направлена на преследуемого, значит производная dy/dx также равна нулю.

Из этих начальных условий определяем значения обеих произвольных постоянных.

(1.4.18)

Окончательно получаем для нашего примера

(1.4.19)

Выражение внутри скобок можно несколько видоизменить, приведя слагаемые к общему знаменателю и вынося за скобки общий множитель.

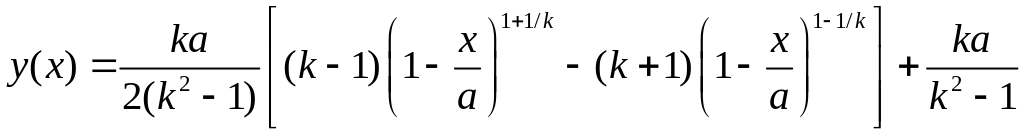(1.4.20)

Интегрирование (1.4.16) при k = 1 дает

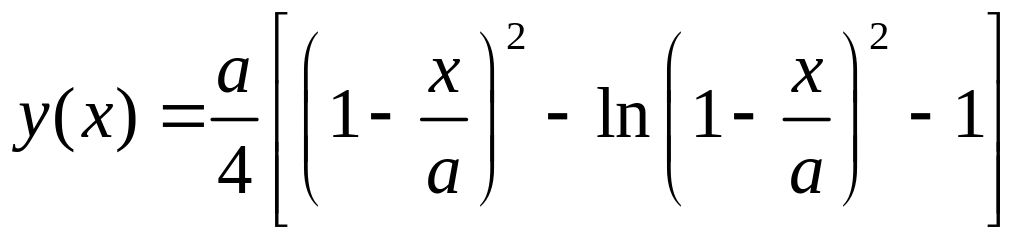(1.4.20)

При k > 1 догоняющий настигнет преследуемого. Значение координаты x, очевидно, будет равно a, значение координаты y , при котором произойдет «долгожданная» встреча из (1.4.20) получается равной

(1.4.21)

При k = 3/2, 2, 3 координата точки перехвата равна соответственно 6a/5, 2a/3,3a/8. Формула для точки перехвата, получаемая как результат вывода формулы кривой погони, показывает неувядаемость аналитических методов.

Агентная модель погони в инструментальной среде Netlogo.

«Мир» Netlogo состоит из агентов. Агенты – это сущности, которые могут выполнять инструкции. Имеется четыре типа агентов:

Черепашки (turtles) - агенты, которые могут перемещаться по «миру» Netlogo.
Пятнышки, лоскутики (patches) – квадратные элементы ландшафта «мира» Netlogo. «Мир» Netlogo двухмерный и образован сеткой, состоящей из лоскутиков;
Связи (links) – агенты, каждый из которых связывает две черепашки. Связи могут быть направленные и не направленные.
Обозреватель (Observer) – не имеет местонахождения в «мире»; с ним можно отождествить себя, наблюдающего со стороны за всем тем, что происходит в «мире».

Инструкции

Инструкции (команды) говорят агентам, что им делать. Инструкции, введенные пользователем, называются процедурами (precedure). Инструкции, реализованные в системе - встроенные процедуры(primitives). Среда Netlogo содержит большой набор встроенных процедур, прекрасно задокументированных и проиллюстрированных примерами.

Пример процедуры, введенной пользователем и присутствующей в каждой программе на языке Netlogo:

to setup

clear-all ;;очищает «мир»

create-turtles 12 ;;создает 12 агентов

end ;; комментарий- достаточно одной «;»

В этом примере setup является процедурой, она вводится пользователем, в то время как clear-all и create-turtles примитивы системы.

В системе имеется аналог того, что в других языках программирования называется функцией – это reporters, который не являются командами, а служат для формирования выходного значения. Например,

to-report average-size

report mean [size] of turtles ; рассчитывает средний рост всех агентов

end

Имеется команда, несущая приказ агентам для выполнения ими. Многие выражаются повелительными глаголами (create, die, move и т.п. ).

Команды, вводимые пользователем как процедуры, содержат отличительную частичку «to» .

Пример,

to go

ask turtles

[ forward 1 ;всем двинуться вперед на 1 шаг

right random 360 ] ;всем повернуться на некоторый угол

end

Инструкция может получать параметры на входе, которые используются для выполнения.

to-report absolute-value [ number] ; ;В скобках – входной параметр

ifelse number >= 0 ; Если число больше нуля

[ report number ] ; то на выход само число

[report 0 – number ] ;иначе нуль или его с ;противоположным знаком

end

Переменная обозначает место, в котором записывается значение – число, текст, список и пр. В Netlogo переменные могут быть глобальные (global), собственные переменные агентов (turtles-own), собственные переменные patches-own , собственные переменные связей (links-own) и локальные переменные внутри процедур. Для изменения значений переменных используется оператор (команда) set.

Значение глобальной переменной известно любому агенту любого типа. Глобальная переменная может быть введена вместе с элементом управления, размещаемым в области диалога (кнопка, переключатель, слайдер, список выбора)- их не надо объявлять словом globals, как в следующем примере:

globals [ number-of-trees ]

Что касается turtle, patch и link переменных, то имеется набор встроенных переменных, но пользователь может также ввести переменные агентов дополнительно к встроенным переменным. Примерами встроенных переменных могут служить color для черепашек, pcolor для лоскутиков. Если мы присваиваем значение этим переменным все(!) агенты получают присваиваемое свойство.

Для черепашки встроенная переменная heading задает направление, при создании черепашки командой create-turtles эта переменная получает случайное значение. Среди других встроенных переменных обратим внимание на переменные, определяющие координаты агентов в «мире» - xcor, ycor для черепашек и pxcor и pycor для лоскутиков.

Встроенные переменные для связей – end1, end2 - агенты, между которыми установлена связь и thickness – сила связи. Полный список в Netlogo Dictionary. Пользовательское определение агентных собственных переменных выполняется следующим образом:

turtles-own [ energy ] ;;каждая черепашка имеет значение энергии

patches-own [sappiness ] ;;каждое пятнышко имеет свою сочность

links-own [ strength ] ;;каждая связь имеет свою силу.

Локальные переменные вводятся и используются только в контексте отдельной процедуры. Для создания локальной переменной используется команда let. Если создание выполнено в начале процедуры, то созданная переменная доступна для использования и изменения везде внутри процедуры. Если переменная создана внутри квадратных скобок, например, в конструкции ask, то она доступна только внутри скобок.

to swap-color [ turtle1, turtle2] ;; на вход сами агенты являются

let temp ([color] of turtle1) ;;запомнить цвет первого агента

ask turtle1 [ set color (([color] of turtle2) ; у первого цвет второго

ask turtle2 [ set color temp) ;у второго цвет первого

end

Глобальная переменная может быть прочитана или изменена в любой момент любым агентом. Каждый агент имеет прямой доступ к своей собственной переменной для чтения и изменения. Если требуется, чтобы агент мог поменять переменную другого агента, то необходимо использовать команду ask.

ask turtle 5 [ show color] ;;просьба Наблюдателя к черепашке 5 показать ;;свой цвет

ask turtle 5 [ set color green ] ;черепашка 5 пусть позеленеет

Можно использовать of, чтобы один агент мог обратиться к переменной другого.

show [color] of turtle 5 ; то же что первая из двух предыдущих команд

Черепашка может читать и изменять переменные того лоскутика, на котором она стоит.

ask turtle [set pcolor red] ;;все пятнышки, на которых стоят ;;черепашки пусть покраснеют

Команда ask служит для того, чтобы задать действие агенту – черепашке ли, пятнышку ли, связи ли. Обычно Обозреватель использует эту команду для всех черепашек и лоскутиков. Вот примеры:

to setup

clear-all ;; очистить «мир»

create-turtles 100 ; наплодить 100 штук агентов

ask turtles

[set color red ; сделать их цвет красным

forward 40 ; отправить их вперед на 40 шагов

]

ask patches

[ if (pxcor > 0) ;;правая половина «мира»

[set pcolor green ] ; пусть позеленеет

]

end

Посредством команды ask необязательно обращаться ко всем агентам, а индивидуально, например:

to setup

clear-all

create-turtles 3 ;; индивидуальные номера, созданных ;;черепашек

;;( встроенная переменная - who ) имеют

; значения -0, 1, 2

ask turtle 0 [fd 10 ] ;; черепашку с номером 0 посылаем вперед

ask turtle 1 [set color brown ] ;; эта пусть примет коричневый цвет

ask patch 2 -1 [set pcolor green] ;; эта пусть зеленеет

ask turtle 0 [create-link-to turtle 2 ] ;; так создается связь от 0-й ко 2-й

ask link 0 2 [set color yellow] ;;она станет желтой как пресса

ask turtle 0 [ask patch-at 1 -1 ;; просьба со стороны черепашке к ;;лоскутику 1 -1

[set pcolor red ] ;; стать красным

]

end

Списки (Lists )

Netlogo находится в русле традиций разработок среды Logo. Неудивительно, что основная концепция структурных данных представлена списками. Список может быть пустым или содержать один или более фрагментов данных. Данные в списках могут относиться к разным типам – числа, строки, списки, агенты, множества агентов (agentset).

Так называемый константный список состоит из констант и представляет набор значений, заключенный в квадратные скобки

Set const-list [1 2 3].

Список может формироваться при выполнении программы, например, посредством, репортера list, который работает так:

Set rand-list list (random 10) (random 20) ;;создать список из двух

;;случайных чисел.

Если нужно создать список с большим числом элементов, то используют круглые скобки как в примере:

Show ( list random 10 random 20 random 30 )

С помощью примитива (встроенной команды) of можно создавать список свойств агентов. Этот список будет содержать значения переменных агентов, указанных с помощью of.

set fitness-list ([fitness] of turtles) ;; список содержит значения

;; переменной fitness oт каждого агента черепашки в ;;случайном порядке.

Часто применяются также конструкции n-values и sentence.

В системе не предполагается изменение списков, но предусмотрена возможность создание новых списков на основе старых. Например:

set my-list [2 7 5 Bob [3 0 -2]] ;; my-list is now [2 7 5 Bob [3 0 -2]]

set my-list replace-item 2 mylist 10 ;; my-list is now [2 7 10 Bob [3 0 -2]]

Смотрите также команды работы со списками: lput, fput, but-last, и but-first.

Две команды осуществляют итеративную обработку всего списка – foreach и map. Команда

foreach [2 4 6]

[ crt ?

show (word "создать " ? " черепашки") ]

приведет к появлению надписи

=> создать 2 черепашки => создать 4 черепашки => создать 6 черепашки

Знак вопроса в рассмотренной конструкции выполняет роль переменной цикла и принимает поочередно значение элементов из списка foreach.

Возможности циклической обработки не исчерпываются данным оператором. В системе имеются удобные конструкции repeat и while .

Набор агентов (agentset)

Все агенты одного набора должны быть одного типа - либо черепашки, либо пятнышки, либо связи. Внутри набора агенты не упорядочены. Можно создавать наборы агентов с определенными специфическими свойствами. Например, все пятнышки с pxcor кратным некоторой величине. Другой пример - все связи, исходящие из какого-то агента.

Turtles –here – набор агентов, расположившихся на данном лоскутике.

Похоже turtles-at с указанием координат лоскутика. Создать набор можно разными способами, главным из которых является описатель breed (создание породы – типа агентов)

Breed (men man)

Имеется и такие способы образования наборов агентов. Вот примеры:

turtles with [color = red] ;; все красные агенты

other turtles-here with [color = red] ;;все иные агенты на моем ;; ;;лоскуте

patches with [pxcor > 0] ;; пятнышки справа

turtles in-radius 3 ;; агенты в радиусе 3

Когда набор обозначен, тогда можно сделать очень полезные вещи с ним:

Используя ask, заставить всех агентов набора что-то сделать
Проверить, есть ли в наборе агенты- не пуст ли он. Для этого в среде предусмотрено- any?
Проверить выполняется некоторое свойство для всех агентов набора с помощью all?
С помощью count вести подсчет количества агентов в наборе.

Вот еще примеры того, что можно делать с наборами

ask one-of turtles [ set color green ]

one-of ;;выбирает случайного агента из \набора

amax-one-of agentset [reporter] ;;выбирает агента с максимальным значением

;;признака

if all? turtles [color = red] ;; все ли красные ?

[ show "every turtle is red!" ] ;; и сообщает эту радостную весть

show [([color] of end1) - ([color] of end2)] of links ;; показать цвет связанных

;; одной связью

Шаблон для многих моделей Netlogo

globals [ … ] ; ;глобальные переменные

turtles-own [ … ] ;;Собственные переменные агентов, объявленные

;;пользователем

patches-own [ … ] ;;То же для лоскутиков «мира

links-own [ … ] ; ;;То же для связей

to setup

clear-all …

setup-patches … setup-turtles … setup-graphs …

end

to go

conduct-observer-procedure …

ask turtles [выполнить turtle-procedure] …

ask patches [выполнить patch-procedure] …

tick

update-plots ;; построение графиков

end

to update-plots

set-current-plot “my-plot”

set-current-plot-pen “my-pen”

plot statistics

set-current-plot “my-XY-plot”

plotxy ticks (count turtles) …

set-current-plot “my-histogram”

histogram [age] of turtles …

end

to-report statistics

report the-result-of-some-formula

end

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 4

Моделирование процессов конкуренции. Модель «хищник-жертва». Влияние внутривидовой конкуренции. Численное и аналитическое решение системы дифференциальных уравнений.

Рассмотрим поведение двух видов, численности которых обозначим соответственно x и y . Условное название для первого вида x – «хищники», для второго y – «жертвы», которые для составителя модели не важны, поскольку важны не слова, а логика поведения, задаваемая следующими формальными соотношениями.

Предположим, что в отсутствии «хищников» жертвы живут и размножаются по экспоненциальному закону.

Y’(t) = a*Y(t) (1.5.1)

Напротив, в отсутствии «взаимодействия» с жертвами и, как следствие, в отсутствие пищи, хищники погибают, и их численность убывает по экспоненциальному закону:

X’(t)=-c*X(t) (1.5.2)

Столкновения особей разных и столь противоположных видов предположительно определяются произведением численностей на момент столкновения. Для одних это гибель, для других пища и источник энергии для продолжения жизни.

В итоге система из данных двух уравнений приобретает вид:

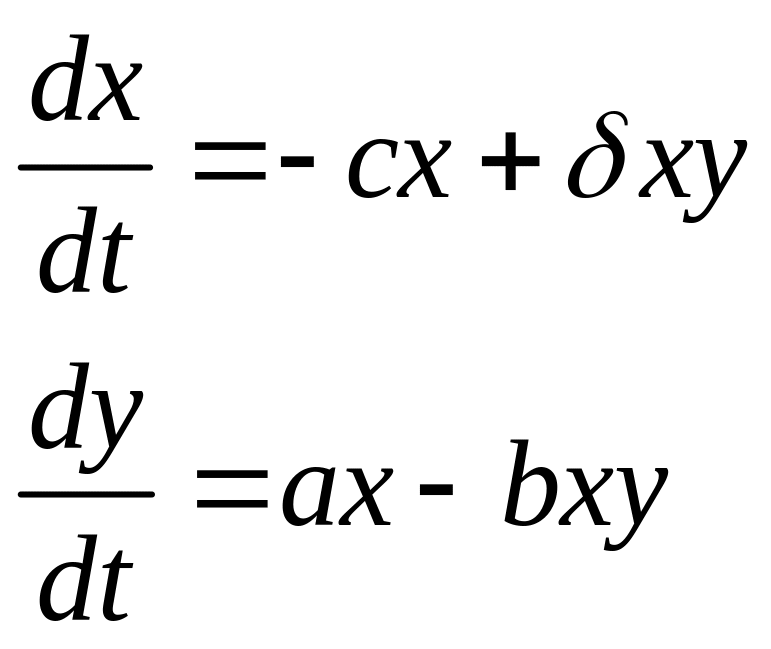(1.5.3)

От данной системы перейдем к одному уравнению, разделив второе на первое.

(1.5.4)

Преобразуем к виду уравнений с разделяющимися переменными

(1.5.5)

Интегрируя, получаем

(1.5.6)

Освобождаемся от логарифмов

(1.5.7)

Произвольная постоянная определяется из начальных условий. Если в начальный момент численности видов были равны соответственно Xo и Yo, то

Если ввести функцию двух переменных

, (1.5.8)

то решение, определяемое начальными условиями, представляется линией уровня функции u(x,y) соответствующей уровню .

2. Символьные вычисления в инструментальной среде MathCad и их использование для решения задач и моделирования.

В среде MathCad имеется удобное средство построения и графического отображения линий уровня функции двух переменных.

Линия уровня, соответствует траектории процесса в фазовом пространстве, и обнаруживают отчетливо циклический характер изменений в системе.

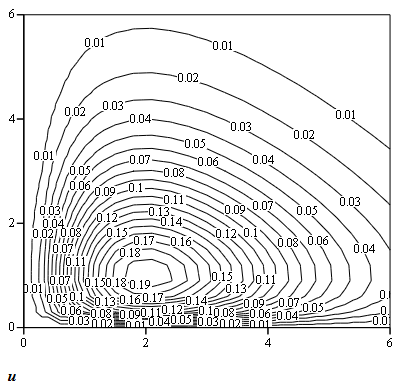
Линии уровня для функции

Приводим также решение системы дифференциальных уравнений нашей модели в той же инструментальной среде MathCad.

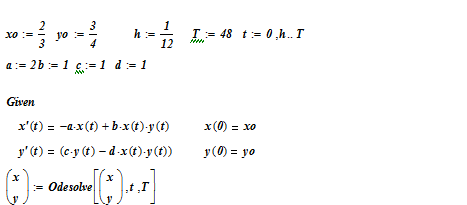
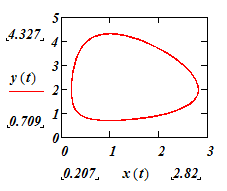
Фазовая траектория развития численностей видов

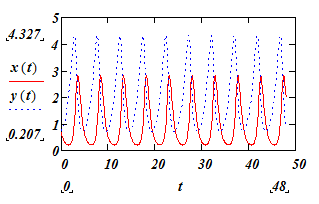
График изменения во времени численностей видов

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 5

Моделирование вероятностных рассуждений с применением байесовских сетей доверия.

Рассмотрим некоторую совокупность объектов, характеризующихся набором номинальных признаков. Если D — множество допустимых значений признака, то номинальный признак – тот для которого множество возможных значений конечно, в отличии от признаков иного типа

(бинарный признак Df = {0,1}; порядковый признак: Df — конечное упорядоченное множество, количественный признак: Df — множество действительных чисел).

Для данного множества известен так называемый классовый или меточный признак, тип которого как правило – бинарный (логический).

Данная совокупность в задаче построения классификатора используется как обучающая выборка, на основании которой строится классификатор новых объектов, то есть объектов, классовый признак которых неизвестен. Результатом работы построенного классификатора является отнесение объекта к некоторому классу (присваивание значения метки класса) и оценка вероятности с которой это отнесение выполнено.

Например, если имеется совокупность данных о претендентах на полет в космос, то в качестве характеристик можно назвать категории веса, роста и и уровня специальной подготовки, а в качестве меточного признака (label в терминологии аналитической библиотеки Weka)) признак пригодности для космической экспедиции Фрагмент обучающей выборки мог бы, в таком случае иметь вид (Таблица 2.4.1).

Признак	Вес	Рост	Подготовка	Годен?
	A	B	С	H
…..	……..	……..	…….	…….
1001	легкий	средний	достаточная	Да
1002	тяжелый	высокий	недостаточная	Нет
1003	тяжелый	средний	достаточная	Да
…….	…….	…….	…….	……

Таблица 2.4.1. Фрагмент обучающей выборки.

Если обучающая выборка содержит 1000 объектов, из которых годными признано 200 , а остальные нет, то априорная вероятность для претендента оказаться в числе признанных пригодными для полета равна 0. 2 (соответственно, оказаться вместе с большинством – 0.8). На основании выборки можно построить статистку по каждому признаку для обеих категорий годности. По этой статистике образуются условные вероятности проявления признака, если известен его класс. Вероятность (среднего роста | пригоден) = P(B|H) и т.д. Задача построения байесовского классификатора решается применением формулы Байеса для расчета условных вероятностей P(H| A&B&C).

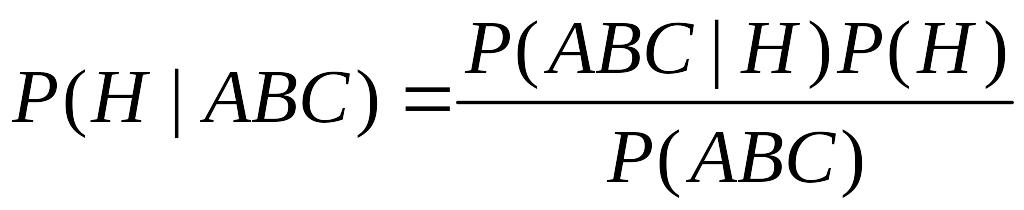(2.4.1)

При этом делается достаточно грубое предположение о независимости случайных величин A,B,C, что позволяет записать вероятности наблюдаемых событий, используя формулу

(2.4.2)

(2.4.3)

Тогда (2.4.1) с учетом (2.4.2) и (2.4.3) получает вид

(2.4.4)

Такой вид подразумевает возможность для независимого и последовательного пересчета по формуле Байеса каждого признака

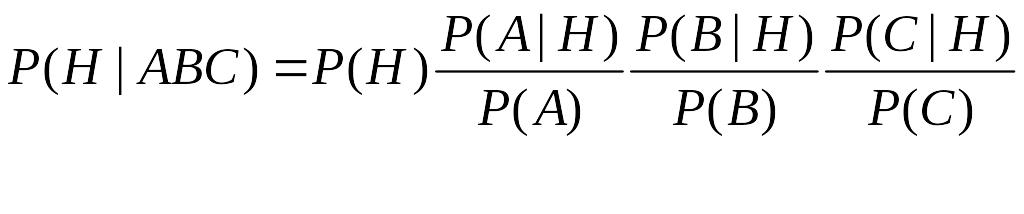(2.4.5)

Последняя формула отлично иллюстрирует то, почему классификатор называется байесовским и почему наивным (наивным в силу сделанного предположения о независимости признаков). Проиллюстрируем построение и работу классификатора в среде GINIE 2/0

Рис. 2.4.1. Условные вероятности признаков для класса «Годен»

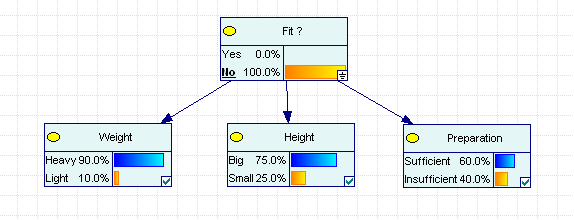
Рис. 2.4.2. Условные вероятности признаков для класса «Не годен».

Данные условные вероятности, как уже отмечалось, получаются из обучающей выборки.

Задаем значения признаков ранее не классифицированного объекта.

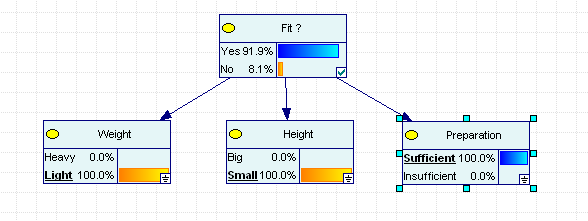
Рис. 2.4.3 . Апостериорные вероятности определяют класс объекта.

Из результатов видно, что для легкого маленького подготовленного претендента вероятность не быть зачислены в космические туристы менее 10%.

Данная задача относится к задачам типа машинного обучения (Machine Learning), которым посвящена четвертая глава пособия.

Вероятностные распределения связанные с моделью простейшего потока событий.

Последовательность событий, происходящих одно за другим в случайные моменты времени, получила название потока событий. Время между событиями потока является случайной величиной. Заодно последовательность событий, происходящих через фиксированный момент времени, также назвали потоком, дав ему в качестве характеристики слово – регулярный поток.

Простейший поток событий – это такой поток, который характеризуется следующими свойствами:

вероятность наступления того или иного числа событий, приходящихся на произвольный промежуток времени, зависит только лишь от длительности данного промежутка, но отнюдь не от расстояния его от начала отсчета;
вероятность наступления того или иного числа событий, приходящихся на произвольный промежуток времени, никак не зависит от наступления или не наступления событий до начала рассматриваемого промежутка;
если промежуток времени можно рассматривать как достаточно малую величину, то вероятность наступления одного события в течение этого малого промежутка приближенно пропорциональна длительности этого промежутка, а вероятностью наступления двух и более событий можно пренебречь

Эти три свойства получили название соответственно свойствами стационарности, отсутствия последействия и ординарности.

С простейшим потоком связана случайная величина (дискретная случайная величина)-число событий потока, поступивших за промежуток времени t. В силу первого свойства (стационарности) вероятность того или иного числа событий зависит только от величины t. Значениями этой случайной величины являются целые числа m = 0,1,2 ….

Соответствующие вероятности обозначим p_m(t).

По определению p_m(t) - вероятность того, что за фиксированный промежуток времени t наступит равно m событий простейшего потока. Для расчета этой вероятности применяется рассуждение, основанное на сравнении вероятностей для исходного промежутка и промежутка, измененного на малую величину (метод вариации промежутка времени).

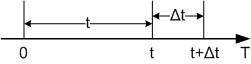
Рис. 3.1.1 Вариация отрезка

В соответствии с третьим свойством простейшего потока вероятность наступления одного события, происходящего в промежутке Δt, можно записать формулой:

, (3.1.1)

где λ – некоторая константа; второе слагаемое в правой части (3.1.1) –есть бесконечно малая более высокого порядка малости, чем Δt.

Это предположение, как следствие, дает следующее соотношение:

(3.1.2)

Вероятность отсутствия событий в промежутке времени t обозначено . Отсутствие событий в промежутке t + Δt означает наступление двух независимых событий – отсутствие в промежутке t и отсутствие событий потока в промежутке Δt (независимость следует из второго свойства простейшего потока). По правилу умножения вероятностей получаем

(3.1.3)

С учетом формул (3.1.2)

(3.1.4)

Раскрываем скобки и переносим в левую часть, затем делим на Δt , Получаем

(3.1.5)

В пределе при Δt ==> 0 получаем для вероятности дифференциальное уравнение

(3.1.6)

с начальным условием . (Это следует прямо из формулы (3.1.2)).

Интегрируя (3.1.6), находим вероятность отсутствия событий за промежуток t.

(3.1.7)

Переходим к расчету вероятности наступления одного события за промежуток t.

Наступление строго одного события в промежутке t+ Δt складывается из двух событий:

наступает одно событие в промежутке t, но не наступает ни одного в промежутке Δt,
единственное событие наступает в промежутке Δt, в промежутке t событий нет.

Помня об отсутствии последействия и как следствие о независимости наступления событий в промежутках t и Δt, получаем соотношение:

(3.1.8)

Используя формулы (3.1.1) и (3.1.2) получаем соотношение

, (3.1.9)

которое преобразуем аналогично тому, как было получено уравнение (3.1.5).

(3.1.10)

и дальше дифференциальное уравнение для вероятности одного события.

(3.1.11)

Начальное условие , функция уже известны к моменту, когда мы приступаем к решению этого уравнения.

Произведем замену . Производная y(t) равна отсюда

(3.1.11)

С учетом (3.1.77) и (3.1.11) имеем

(3.1.12)

Интегрируя с учетом начального условия y(0) = 0 получаем

(3.1.13)

и далее

(3.1.14)

Мы не будем рассматривать отдельно расчет вероятности , а проведем рассуждения для произвольного m – в промежутке времени t.

За промежуток времени t+Δt строго m событий может произойти при следующих взаимоисключающих случаях:

в промежутке t произошло m событий и «одновременно» (в смысле в уме одновременно) в промежутке ни одного;
в промежутке t произошло m -1 событий, а в промежутке одно;
в промежутке t произошло m-2 событий, а в промежутке два события;

Здесь следует оборвать перечисление, так как уже два события в силу ординарности потока имеют пренебрежимо малую вероятность произойти за малый промежуток. Тем это очевиднее при более двух событиях. Проведенное рассуждение приводит к соотношению похожему на (3.1.8):

(3.1.15)

С ним проводим преобразования, которые неукоснительно приводят к дифференциальному уравнению:

(3.1.16)

Начальные условия .

Получена система дифференциальных уравнений, для решения которой можно применить замену, аналогичную (3.1.11).

, (3.1.17)

благодаря которой (замене) система преобразуется к виду (легко доказывается по индукции)

(3.1.18)

В итоге получаем

(3.1.19)

Последняя формула выражает закон распределения Пуассона – закон распределение вероятностей дискретной случайной величины, а именно числа событий за промежуток времени t.

Рис. 3.1.2 Распределение Пуссона

На рисунке 3.1.2 представлено распределения Пуассона при заданных частных значениях параметров.

Характер распределения при различных λ иллюстрируется на Рис 3.1.3.

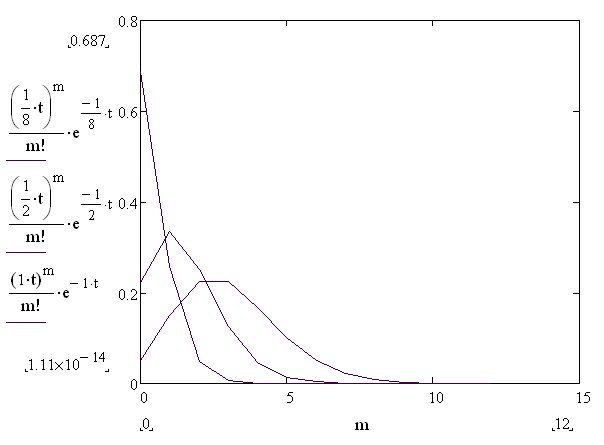
Рис . 3.1.3 Распределение Пуассона при различных λ.

Следующая графическая иллюстрация простейшего потока поможет дать интерпретацию параметру λ распределения Пуассона. Возьмем t равным единице (t=1) и разобьем промежуток [0;t] на достаточно большое число N, так чтобы полученные промежутки длиной 1/N можно было бы считать малыми в смысле свойства ординарности потока. Тогда на каждом промежутке возможно появление одного события либо отсутствие события. Тогда из формулы (3.1.1) следует (если заменить Δt на 1/N)

(3.1.20) И если учесть, что p₁ – это в некотором смысле частота, то λ – приобретает смысл интенсивности потока, то есть среднего числа событий в единицу времени.

С простейшим потоком связана еще одна случайная величина – время между последовательными событиями. По своей природе данная величина является непрерывной случайной величиной. Найдем функцию распределения этой случайной величины.

Функция распределения F(x) случайной величины ξ определяется как вероятность события, состоящего в том, что значение случайной величины меньше x.

F(x) = P(ξ < x) Из определения F(x) следует, что функция эта монотонно возрастает от нуля до 1.

Найдем вероятность того, что случайная величина τ – время между последовательными событиями меньше t.

F(t) = P (τ < t ) (3.1.21)

Очевидно, что F(t) = 1 - P( τ >= t ). В свою очередь P( τ >= t ) – означает, что в промежутке t не было событий, а это значит, что (см. формулу (3.1.7))

F(t) = 1 – p₀(t) = 1- e^-^λt (3.1.22)

Плотность распределения для этой случайной величины существует и выражается формулой

F’(t) = f(t) = λ e^-^λt (3.1.23) На следующем рисунке дана графическая иллюстрация полученных формул.

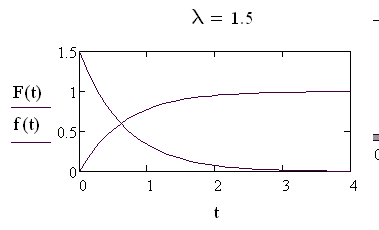
Рис. 3.1.4. Случайная величина, распределенная по экспоненциальному закону

На рисунке 5 точками показаны моменты наступления событий, время между которыми имеет экспоненциальный закон распределения.

Рис. 3.1.5 Время между событиями

Зная закон распределения вычислим параметры распределения – математическое ожидание и среднеквадратичное отклонение. Вычисление математического ожидания производится, как известно, интегрированием выражения

(3.1.24)

Обратная величина от параметра – это среднее время между поступлениями событий потока, что еще раз оправдывает понимание этого параметра как интенсивности - количества событий в единицу времени.

Вычисление дисперсии осуществляется по формуле

(3.1.25)

и, следовательно, среднеквадратичное отклонение для показательного закона равно математическому ожиданию.

Показательный (в смысле экспоненциальный) закон, таким образом, относится к классу однопараметрических законов распределения. Статистический смысл параметра распределения - это величина обратная среднему времени между последовательными событиями.

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 6

«Наивный» байесовский классификатор.

Признак	Вес	Рост	Подготовка	Годен?
	A	B	С	H
…..	……..	……..	…….	…….
1001	легкий	средний	достаточная	Да
1002	тяжелый	высокий	недостаточная	Нет
1003	тяжелый	средний	достаточная	Да
…….	…….	…….	…….	……

Таблица 2.4.1. Фрагмент обучающей выборки.

(2.4.1)

(2.4.2)

(2.4.3)

Тогда (2.4.1) с учетом (2.4.2) и (2.4.3) получает вид

(2.4.4)

(2.4.5)

Рис. 2.4.1. Условные вероятности признаков для класса «Годен»

Рис. 2.4.2. Условные вероятности признаков для класса «Не годен».

Данные условные вероятности, как уже отмечалось, получаются из обучающей выборки.

Задаем значения признаков ранее не классифицированного объекта.

Рис. 2.4.3 . Апостериорные вероятности определяют класс объекта.

2. Программное обеспечение для математического моделирования -обзор .

Deductor является аналитической платформой - основой для создания законченных прикладных решений. Реализованные в Deductor технологии позволяют на базе единой архитектуры пройти все этапы построения аналитической системы: от создания хранилища данных до автоматического подбора моделей и визуализации полученных результатов.

Deductor предоставляет аналитикам инструментальные средства, необходимые для решения самых разнообразных аналитических задач: корпоративная отчетность, прогнозирование, сегментация, поиск закономерностей - эти и другие задачи, где применяются такие методики анализа, как OLAP, Knowledge Discovery in Databases и Data Mining. Deductor является идеальной платформой для создания систем поддержки принятия решений. Реализованные в Deductor технологии могут использоваться как в комплексе, так и по отдельности для решения широкого спектра бизнес-проблем:

Системы корпоративной отчетности.

Обработка нерегламентированных запросов. Анализ тенденций и закономерностей, планирование, ранжирование. Прогнозирование. Управление рисками.

ExtendSim самый мощный и гибкий инструмент моделирования программного обеспечения на рынке. СМО. Визуальная среда иммитационного моделирования для компьютерной реализации набора моделей.

Аналитическая Платформа Deductor является основой для создания прикладных аналитических решений. Реализованные в ней технологии позволяют пройти все этапы построения аналитической системы от создания хранилища данных до автоматического подбора моделей и визуализации полученных результатов, используя одну систему. (прогнозирование, оптимизация, консолидация данных, аналитическая отчетность, логистика, бюджетирование)

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 7

Нейронные сети в задачах анализа данных и извлечения знаний. Нейронная сеть прямого распространения (многослойный персептрон). Алгоритмы «обучения! нейронной сети.

В качестве «учителя» выступает (как и для всех задач класса Machine Learning) обучающая выборка – набор примеров (прецедентов, фактов), каждый из которых содержит известные значения как параметров входных, так и выходных. Необходимо построить модель, пусть абсолютно непрозрачную в смысле ее устройства, которая бы выполняла над новыми примерами действия сходные с теми, которым подверглись примеры в выборке.

Для понимания работы сети формальных нейронов лучше не опираться на исторически сложившуюся аналогию с «естественными нейронами», поскольку это может только ввести в заблуждение. На рисунке (рис. 4.3.1) представлена схема формального нейрона – простой автомат, который осуществляет преобразование поступающей на его вход данных в результирующий выходной сигнал.

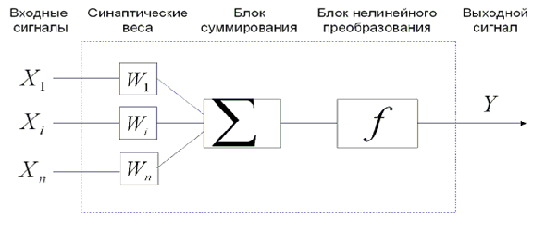
Рис. 4.5.1 . Формальный («искусственный» ) нейрон.

Автомат имеет регистр памяти, в которой находятся числа – веса нейрона. Их величина изменяется в ходе обучения нейрона – цепи управления значениями весов на схеме не показаны, хотя они существенны для работы нейрона. Действие, производимое нейроном, состоит в подсчете взвешенной суммы поступающих сигналов. Полученный на выходе блока суммирования сигнал претерпевает преобразование в блоке нелинейного преобразования. Таким образом, работу нейрона можно описать формулой:

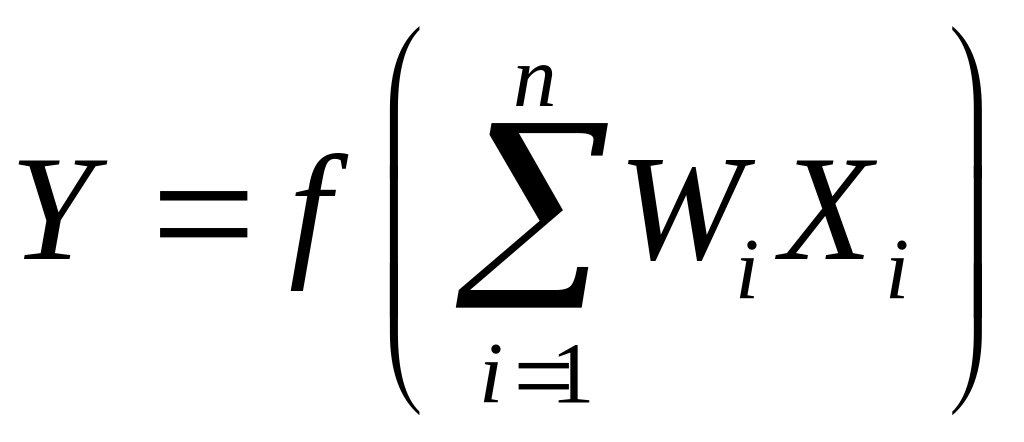(4.5.1)

В этой формуле n – число поступающих на вход сигналов. В качестве функции, осуществляющей нелинейное преобразование, часто используется функция -

(4.5.2)

Параметр γ определяет «крутизну» преобразующей функции. График функции имеет вид-

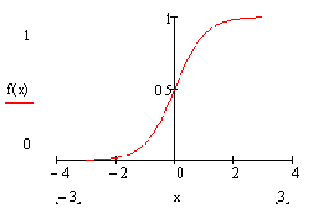
Рис. 4.5.2 График f(x)

Нейроны являются «строительными кирпичиками» для нейронных сетей. Простейшая сеть – так называемый персептрон или сеть прямого распространения, состоит из последовательных слоев нейронов. Кроме нейронов входного слоя и выходного слоя в сети могут быть внутренние слои. На вход нейронов каждого слоя поступают входные сигналы от всех нейронов предыдущего слоя, Ниже на рисунке 4.5.3 представлена сеть прямого распространения, содержащая один внутренний слой четырьмя нейронами. Сеть предназначена для приема трех входных величин и отправления на выход двух результирующих величин.

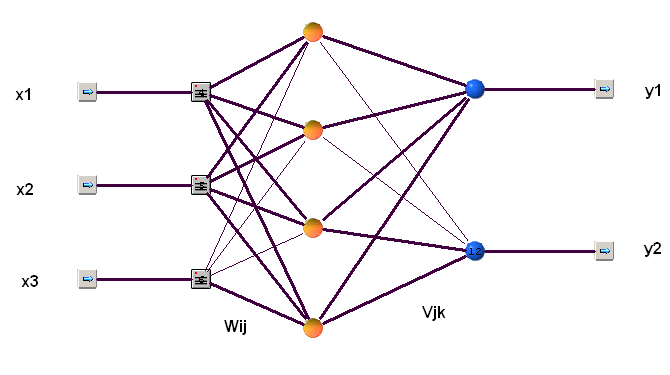
Рис. 4.5.3. Нейронная сеть прямого распространения.

В качестве «учителя» для этой нейронной сети пусть выступают данные из обучающей выборки, фрагмент которой представлен в Таблице 4.5.1.

X1	X2	X3	Y1	Y2
14	14	669	0	697
4	1	386	-3	391
7	25	675	18	707
2	1	642	-1	645
2	33	690	31	725
0	74	49	74	123
7	56	657	49	720
2	96	647	94	745
4	70	694	66	768
7	81	391	74	479
8	27	901	19	936

Таблица 4.5.1. «Обучающая выборка»для нейронной сети

В начале работы веса всех нейронов сети получают случайные значения. Первая поступившая запись формирует выходы сети по формулам (4.5.1). В результате сравнения выходов, рассчитанных сетью (Y_k) , с правильными (y_k) значениями выходов из обучающей выборки вычисляется ошибка

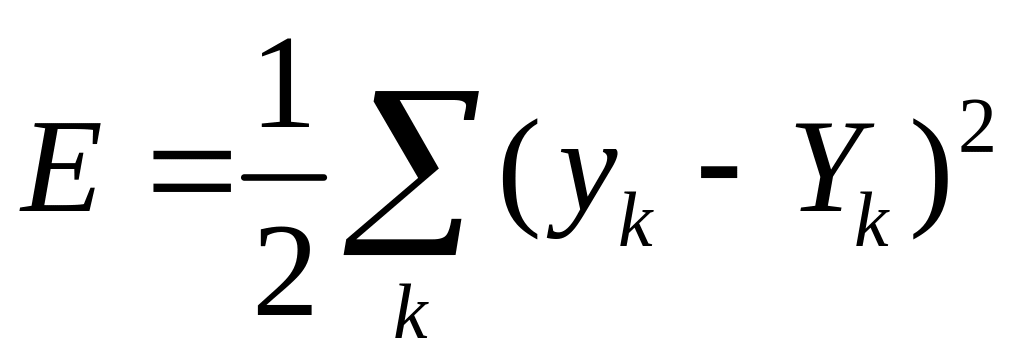(4.5.3)

Данная ошибка есть функция весов сети , и используется для коррекции весов.

Существует два типовых режима коррекции весов –

- после каждой новой записи;

- в конце чтения всех записей из обучающей выборки на основе накопленной ошибки.

При коррекции используется алгоритм минимизации ошибки, являющийся реализацией градиентного метода поиска минимума функции нескольких переменных. В практике нейронных сетей этот метод применяется для коррекции весов по слоям, начиная от нейронов выходного слоя к первому внутреннему слою. В такой форме этот метод получил название метода обратного распространения ошибки. Разберемся в работе алгоритма обратного распространения ошибки на примере нейронной сети, изображенной на рис. 4.5.3.

Входные сигналы обозначим заглавные буквы - , а выходные сигналы от сумматоров первого скрытого слоя – маленькими буквами

Используя обозначения индексов соответственно i – для входных сигналов и j – для выходов от сумматоров запишем (n – количество входных значений, в нашем примере n=3)

(4.5.4)

Для выходных значений скрытого слоя используем обозначение Для выходного слоя последние являются входами; обозначим выходные сигналы сумматоров выходного слоя как и запишем

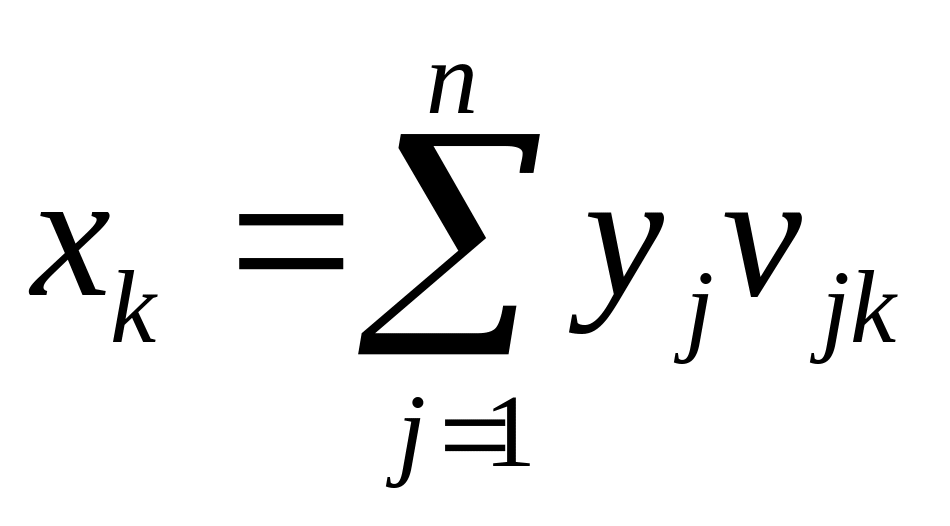(4.5.5)

(4.5.6)

Пускай не вызывает никаких недоразумений использование для разных слоев одинаковых обозначений – сопровождающий индекс будет дополнительным обозначением. Имея выходы (4.5.6) для очередной записи считаем ошибку для этого шага (4.5.3). Если выбран режим коррекции весов после чтения всех записей обучающей выборки, то ошибки (4.5.6) суммируются по всем записям выборки. Применение градиентного метода для выходного слоя даёт:

(4.5.17)

Производная в (4.5.17) вычисляется по правилу дифференцирования сложной функции:

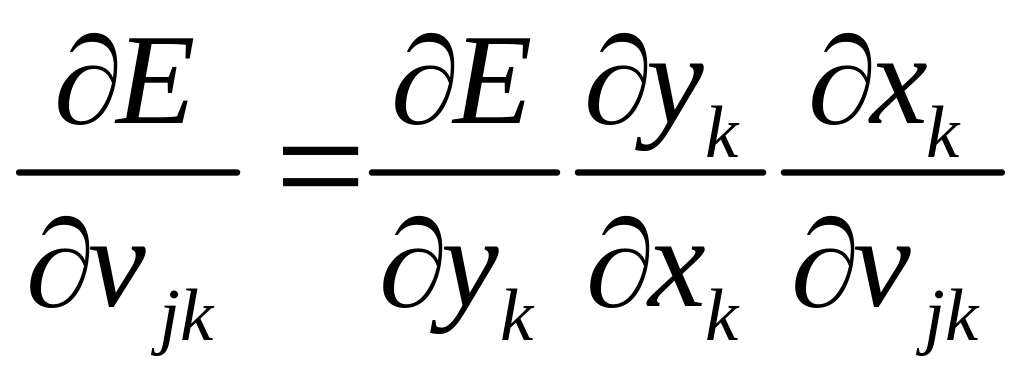(4.5.8)

Наиболее просто считается 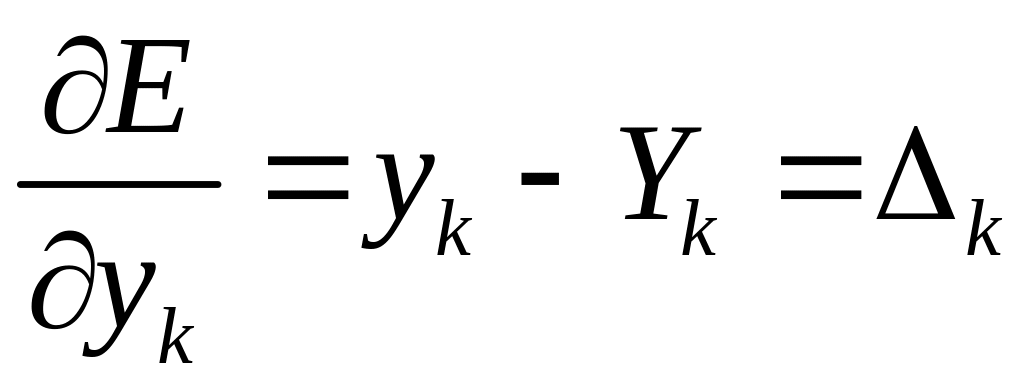, что прямо вытекает из (4.5.3).

В силу известного свойства логистической функции ее производная равна произведению ее самой на ее дополнение до единицы, а потому имеем:

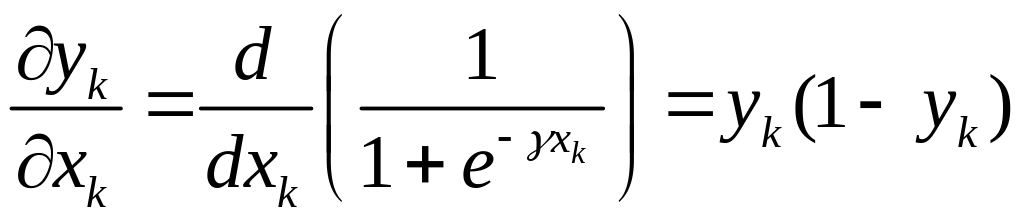(4.5.9)

Наконец, учитывая (4.5.4) получим

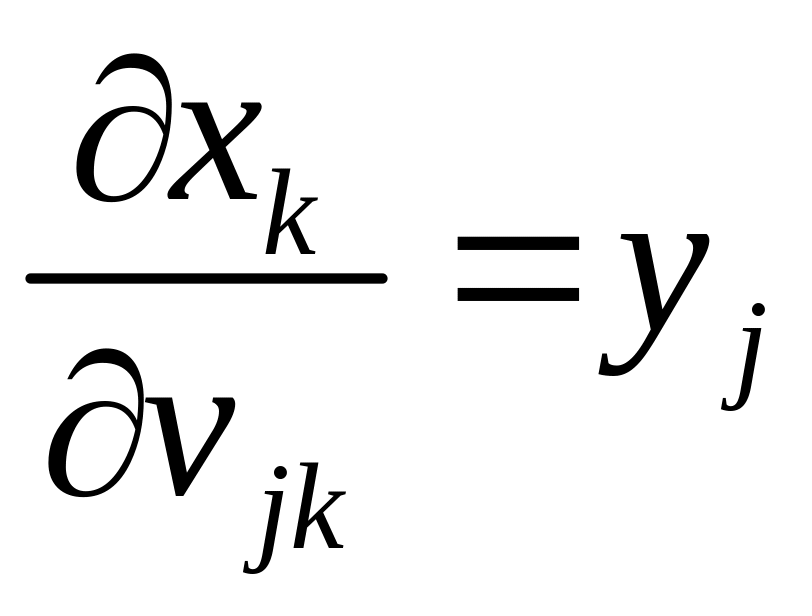(4.5.10)

Индекс j - свидетель того, что величина поступила с предыдущего слоя. Имеем из (4.5.8)

(4.5.11)

(4.5.12)

Коррекция весов выходного слоя выполнена применением (4.5.12).

Для предыдущего слоя перестройка весов производится по формулам:

(4.5.13)

(4.5.14)

(4.5.15)

В (4.5.15) первый сомножитель выразим по правилам дифференцирования сложной функции

а второй сомножитель из (4.5.6) (4.5.16)

Из (4.5.4) имеем (4.5.17)

Аналогично из (4.5.9) 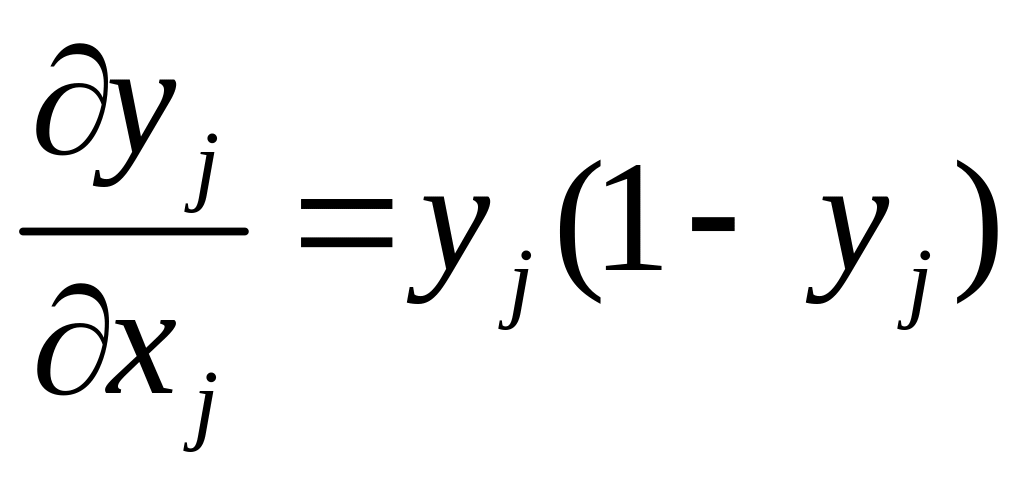(4.5.18)

В итоге (4.5.19)

(4.5.20)

В последней формуле для расчета коррекции весов используется поправка, подсчитанная на первой стадии коррекции и ошибка, которая внедрилась в расчетную формулу для коррекции весов скрытого слоя. Этот факт и дал название алгоритму - метод обратного распространения ошибки.

X1	X2	X3	Y1	Y2	Y1_OUT	Y2_OUT	Y1_ERR	Y2_ERR
14	14	669	0	697	12.06	758.11	0.0145	0.0042
4	1	386	-3	391	11.82	349.19	0.0220	0.0020
7	25	675	18	707	15.15	746.47	0.0008	0.0018
2	1	642	-1	645	9.25	676.99	0.0105	0.0012
2	33	690	31	725	23.00	752.64	0.0064	0.0009
0	74	49	74	123	77.90	223.05	0.0015	0.0113
7	56	657	49	720	50.97	754.64	0.0004	0.0014
2	96	647	94	745	79.77	756.28	0.0203	0.0001
4	70	694	66	768	70.43	796.98	0.0020	0.0010
7	81	391	74	479	77.56	428.94	0.0013	0.0028
8	27	901	19	936	16.38	911.54	0.0007	0.0007

Таблица 4.5.2. Результат «обучения» нейронной сети.

Результат обучения нейронной сети для порции данных из обучающей выборки представлен в Таблице 4.5.2. Результат для нейронных сетей отличный.

В искусстве настройки мастера нейронных сетей нужно выбирать число слоев, количество нейронов в слое, константы h –скорость обучения, крутизны нелинейность вид нелинейности, число просмотров обучающей выборки («эпох» в сложившейся терминологии нейронных сетей). Все указанные элементы не имеют строгого обоснования и их выбор оправдывается достижением результатов.

Методы решения задач при многих критериях предпочтений

Постановка всякой задачи многокритериального выбора включает

1) множество возможных решений X ,

2) векторный критерий f вида (1.1),

3) отношение предпочтения _X .

Само ЛПР в постановку задачи многокритериального выбора не вклю-

чено. В этом нет необходимости. Подразумевается, что все его устремления,

вкусы, пристрастия и предпочтения, оказывающие влияние на процесс

выбора, «материализованы» в терминах векторного критерия и отношения

предпочтения.

Задача многокритериального выбора состоит в отыскании множества

выбираемых решений C(X) , C(X)A X , с учетом его отношения предпоч-

тения _X на основе заданного векторного критерия f , отражающего набор

целей ЛПР.

Приведенная задача многокритериального выбора выписана в терминах

решений. Нередко данную задачу формулируют в терминах векторов. В таком

случае она содержит два объекта

1) множество возможных векторов Y,Y A Rm ,

2) отношение предпочтения _Y ,

и заключается в отыскании множества выбираемых векторов C Y ( ),

C(Y)AY , с учетом отношения предпочтения ЛПР _Y .

Как указано выше, две приведенные задачи (в терминах решений и в

терминах векторов) в указанном выше смысле эквивалентны, поэтому, руко-

водствуясь соображениями удобства, имеет смысл изучать любую из них, а

затем в случае необходимости полученные результаты всегда можно перефор-

мулировать в терминах другой задачи.

(важными являются критерии оптимальности, критерйи эффективности или целевые фун-

кции)

В упрощенном виде задача векторной оптимизации формируется следующим образом:

Имеется n конкурирующих решений:

{S_i} = {S₁, S₂, ..., S_n}, т.е. стратегий, структур, проектов, плакатов и т.д. и m частных критериев

{K_j} = {K₁, K₂, ..., K_m}, не всегда согласованных между собой и противоречивых.

Для оценки конкурирующих решений по частным критериям используются различные средства: экспертные процедуры, мат. моделирование, натуральные эксперименты. При этом множество конкурирующих решений отображается в матрицу векторных оценок:

	S₁	S₂	...	S_n
[k_ji] =	k₁₁	k₁₂	...	k_1n
	k₂₁	k₂₂	...	k_1n
	...	...	...	...
	k_m1	k_m2	...	k_mn

Исходя из матрицы векторных оценок и системы предпочтений ЛПР выбирается рациональное решение.

E = opt_Sj {[k_ji], система предпочтений ЛПР} следовательно S_rat

opt — некоторый оператор векторной оптимизации.

Выбор рационального решения связан с преодолением неопределенностей, которые имеются в связи с наличием многих критериев. Эта неопределенность является принципиальной. Для ее компенсации есть лишь одна единственная возможность: использование системы предпочтений ЛПР (т.е. дополнительной, субъективной информации).

Использование субъективной информации ЛПР позволяет преодолеть принципиальные трудности и выбрать рациональный критерий.

Все множество методов векторной оптимизации можно разбить на 5 классов.

Методы, основанные на формализации, в виде задач математического программирования.
Методы, основанные на реинжинировании критериев и их последовательном применении.
Методы, использующие обобщенный критерий для сравнительной оценки альтернатив.
Методы, не использующие обобщенный критерий для сравнительной оценки альтернатив.
Методы, реализующие процессы структуризации и адаптации при выборе рациональных решений.

Методы расположены в порядке возрастания их потенциальной характеристики (классификационный признак — полнота реализации принципа системности). Методы 1-го и 2-го класса не реализуют в полной мере принцип системности. Методы 3-го класса достаточно конструктивны (их легко использовать), однако не всегда удается обосновать и построить обобщенный критерий. Методы 4-го класса более прогрессивны, т.к. они предусматривают активное использование ЛПР в процессе анализа альтернатив. Методы 5-го класса отражают современные тенденции в области векторной оптимизации и находят применение в современных перспективных интерактивных автоматизированных системах.

АСНИ, САПР, АСЛПР, ... поддержки принятия решений.

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 8

1. Самоорганизующаяся карта Кохонена, применение для выявления групповой структуры данных.

Самоорганизующиеся карты – это одна из разновидностей нейросетевых алгоритмов. Основным отличием данной технологии от рассмотренных нами ранее нейросетей, обучаемых по алгоритму обратного распространения, является то, что при обучении используется метод обучения без учителя, то есть результат обучения зависит только от структуры входных данных. (выполняющая задачу визуализации и кластеризации.) Нейронные сети данного типа часто применяются для решения самых различных задач, от восстановления пропусков в данных до анализа данных и поиска закономерностей, например, в финансовой задаче.

Самоорганизующаяся карта состоит из компонент, называемых узлами или нейронами. Их количество задаётся аналитиком. Каждый из узлов описывается двумя векторами. Первый — т. н. вектор веса m, имеющий такую же размерность, что и входные данные. Второй — вектор r, представляющий собой координаты узла на карте. Обычно узлы располагают в вершинах регулярной решётки с квадратными или шестиугольными ячейками.

Изначально известна размерность входных данных, по ней некоторым образом строится первоначальный вариант карты. В процессе обучения векторы веса узлов приближаются к входным данным. Для каждого наблюдения (семпла) выбирается наиболее похожий по вектору веса узел, и значение его вектора веса приближается к наблюдению. Также к наблюдению приближаются векторы веса нескольких узлов, расположенных рядом, таким образом если в множестве входных данных два наблюдения были схожи, на карте им будут соответствовать близкие узлы. Циклический процесс обучения, перебирающий входные данные, заканчивается по достижении картой допустимой (заранее заданной аналитиком) погрешности, или по совершении заданного количества итераций.

[править]Работа сети

Инициализация карты, то есть первоначальное задание векторов веса для узлов.

Цикл:

Выбор следующего наблюдения (вектора из множества входных данных).

Нахождение для него лучшей единицы соответствия (best matching unit, BMU, или Winner) — узла на карте, вектор веса которого меньше всего отличается от наблюдения (в метрике, задаваемой аналитиком, чаще всего, евклидовой).

Определение количества соседей BMU и обучение — изменение векторов веса BMU и его соседей с целью их приближения к наблюдению.

Определение ошибки карты.

Алгоритм

Инициализация

Наиболее распространены три способа задания первоначальных весов узлов:

Задание всех координат случайными числами.

Присваивание вектору веса значение случайного наблюдения из входных данных.

Выбор векторов веса из линейного пространства, натянутого на главные компоненты набора входных данных.

Цикл

Пусть — номер итерации (инициализация соответствует номеру 0).

Выбрать произвольное наблюдение из множества входных данных.

Найти расстояния от него до векторов веса всех узлов карты и определить ближайший по весу узел . Это — BMU или Winner. Условие на :

для любого , где — вектор веса узла . Если находится несколько узлов, удовлетворяющих условию, BMU выбирается случайным образом среди них.

Определить с помощью функции (функции соседства) соседей и изменение их векторов веса.

Задание

Функция определяет "меру соседства" узлов и и изменение векторов веса. Она должна постепенно уточнять их значения, сначала у большего количества узлов и сильнее, потом у меньшего и слабее. Часто в качестве функции соседства используется гауссовская функция:

где — обучающий сомножитель, монотонно убывающий с каждой последующей итерацией (то есть определяющий приближение значения векторов веса BMU и его соседей к наблюдению; чем больше шаг, тем меньше уточнение);

, — координаты узлов и на карте;

— сомножитель, уменьшающий количество соседей с итерациями, монотонно убывает.

Параметры , и их характер убывания задаются аналитиком.

Более простой способ задания функции соседства:

если находится в окрестности заранее заданного аналитиком радиуса, и 0 в противном случае.

Функция равна для BMU и уменьшается с удалением от BMU.

Изменение векторов веса

Изменить вектор веса по формуле:

Т.о. вектора веса всех узлов, являющихся соседями BMU, приближаются к рассматриваемому наблюдению.

Вычисление ошибки карты

Например, как среднее арифметическое расстояний между наблюдениями и векторами веса соответствующих им BMU:

где N - количество элементов набора входных данных.

2. Численные методы решения систем дифференциальных уравнений.

Ставится задача получения приближенных решений обыкновенных дифференциальных уравнений первого порядка с заданными начальными условиями. Уделяется внимание различным способам вывода численного метода Эйлера, являющегося наиболее простым частным случаем нескольких групп численных процессов разной идеологии. Рассматриваются непосредственные модификации методов Эйлера; одна из таких модификаций, называемая исправленным методом Эйлера, приводит к семейству методов Рунге-Кутты второго порядка. Записывается общий вид формул Рунге-Кутты произвольного порядка, дается геометрическая интерпретация классического метода Рунге—Кутты четвертого порядка, обсуждаются вопросы пошагового контроля точности при реализации методов, приводится алгоритм Кутты—Мерсона, решающий проблему автоматического выбора расчетного шага при численном интегрировании поставленной начальной задачи с заданной точностью.

14.1. Постановка задачи. Классификация приближенных методов. Метод последовательных приближений

Будем рассматривать обыкновенное дифференциальное уравнение (ОДУ) первого порядка

, (14.1)

с начальным условием

у(х_о) = у_о, (14.2)

где f(x, у) — некоторая заданная, в общем случае, нелинейная функция двух переменных. Будем считать, что для данной задачи (14.1)—(14.2), называемой начальной задачей или задачей Коши, выполняются требования, обеспечивающие существование и единственность на отрезке [х_о,Ь] ее решения у = у(х) (такие требования можно найти в любом курсе дифференциальных уравнений или в соответствующем разделе курса высшей математики, см., например [109, 164, 166]). Более того, не оговаривая это отдельно, будем предполагать, что искомое решение обладает той или иной степенью гладкости, необходимой для построения и «законного» применения того или иного метода.

Несмотря на внешнюю простоту уравнения (14.1), решить его аналитически, т.е. найти общее решение у = у(х, С) с тем, чтобы затем выделить из него интегральную кривую у = у(х), проходящую через заданную точку (х_о;у_о), удается лишь для некоторых специальных типов таких уравнений, описание которых также можно обнаружить, например, в упомянутых литературных источниках. Поэтому, как и в родственной для (14.1)-(14.2) задаче вычисления интегралов, приходится делать ставку на приближенные способы решения начальных задач для ОДУ, которые можно разделить на три группы:

приближенно-аналитические методы;
графические или машинно-графические методы;
численные методы.

К методам первой группы относят такие, которые позволяют находить приближение решения у(х) сразу в виде некоторой «хорошей» функции φ(х). Например, широко известен метод степенных рядов, в одну из реализаций которого заложено представление искомой функции у(х) отрезком ряда Тейлора, где тейлоровские коэффициенты, содержащие производные высших порядков, находят последовательным дифференцированием самого уравнения (14.1) [62, 100 и др.]. Другим представителем этой группы методов является метод последовательных приближений, суть которого приведена чуть ниже.

Название графические методы говорит о приближенном представлении искомого решения у(х) на промежутке [x_о,b] в виде графика, который можно строить по тем или иным правилам, связанным с графическим толкованием данной задачи. Физическая или, возможно, точнее будет сказать, электротехническая интерпретация начальных задач для определенных видов уравнений лежит в основе машинно-графических методов приближенного решения. Реализуя на физико-техническом уровне заданные электрические процессы, на экране осциллографа наблюдают поведение решений дифференциальных уравнений, описывающих эти процессы. Изменение параметров уравнений приводит к адекватному изменению поведения решений, что положено в основу специализированных аналоговых вычислительных машин (АВМ).

Наконец, наиболее значимыми в настоящее время, характеризуемое бурным развитием и проникновением во все сферы человеческой деятельности цифровой вычислительной техники, являются численные методы решения дифференциальных уравнений, предполагающие получение числовой таблицы приближенных значений y_i искомого решения у(х) на некоторой сетке значений аргумента х. Этим способам и будет посвящено дальнейшее изложение. Что делать с получаемыми численными значениями решения, зависит от прикладной постановки задачи. Если речь идет о нахождении только значения у(b), тогда точка b включается как конечная в систему расчетных точек x_t, и все приближенные значения у_i ≈ у(х_i), кроме последнего, участвуют лишь как промежуточные, т.е. не требуют ни запоминания, ни обработки. Если же нужно иметь приближенное решение у(х) в любой точке х, то для этого к получаемой числовой таблице значений у_i можно применить какой-либо из способов аппроксимации табличных функций, рассмотренных ранее, например, интерполяцию (гл.8) или сплайн-интерполяцию (гл.11). Возможны и другие использования численных данных о решении.

Коснемся одного приближенно-аналитического способа решения начальной задачи (14.1)—(14.2), в котором искомое решение у = у(х) в некоторой правой окрестности точки x₀ является пределом последовательности получаемых определенным образом функций у_п(х).

Проинтегрируем левую и правую части уравнения (14.1) в границах от x₀ до x:

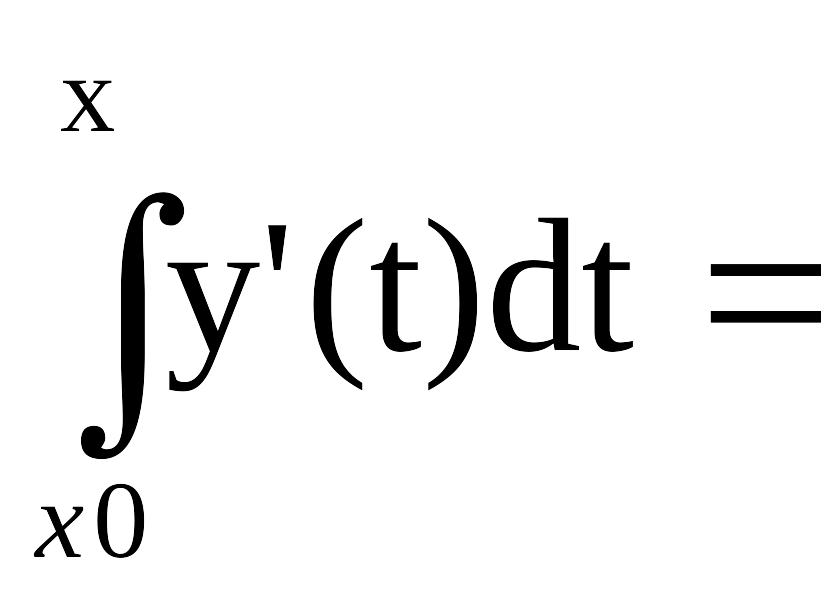
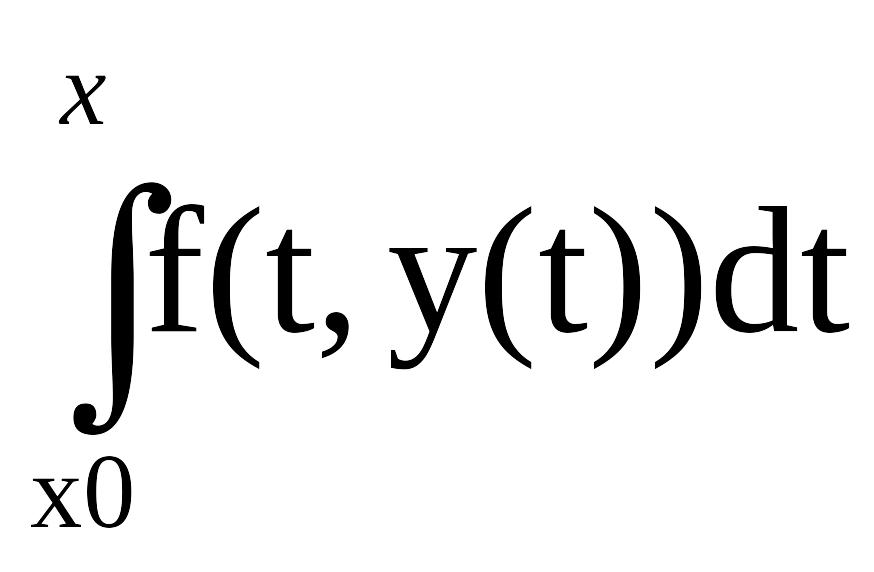Отсюда, с учетом того, что одной из первообразных для у'(х) служит у(х), получаем

или, с использованием начального условия (14.2),

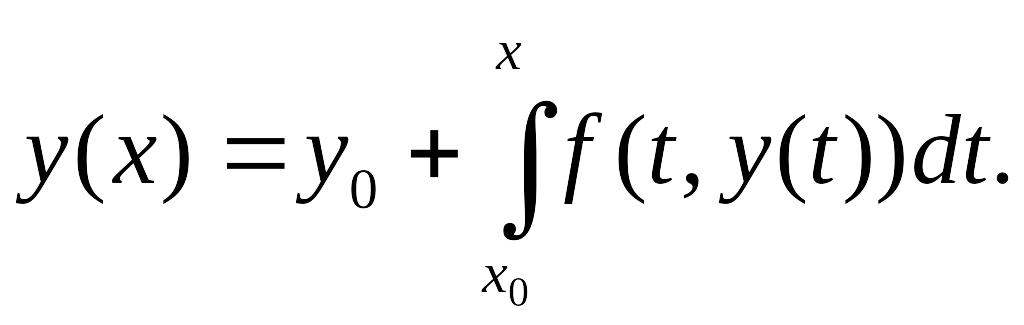
(14.3)

Таким образом, данное дифференциальное уравнение (14.1) с начальным условием (14.2) преобразовалось в интегральное уравнение (неизвестная функция здесь входит под знак интеграла; несколько более подробно об этом см. гл.18).

Полученное интегральное уравнение (14.3) имеет вид задачи о неподвижной точке

для оператора 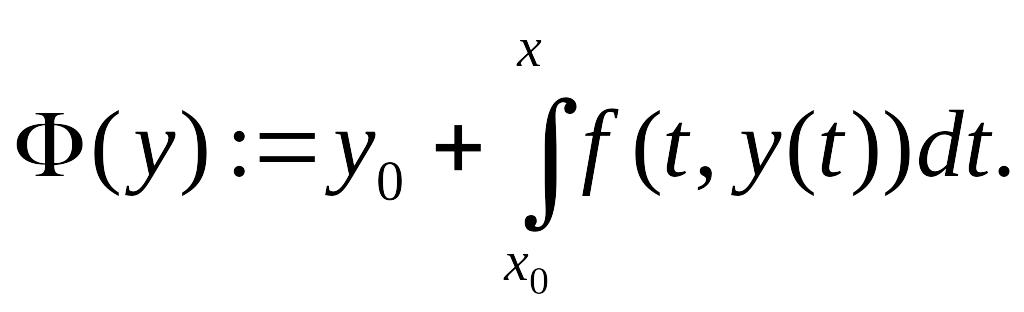Формально к этой задаче можно применить метод простых итераций

(14.4)

14.4

достаточно обстоятельно рассматривавшийся в гл. 3, 6, 7 применительно к скалярным уравнениям, а также к системам линейных и нелинейных алгебраических и трансцендентных уравнений. Беря в качестве начальной функции y_о(х) заданную в (14.2) постоянную y₀, по формуле (14.4) при п = 0 находим первое приближение

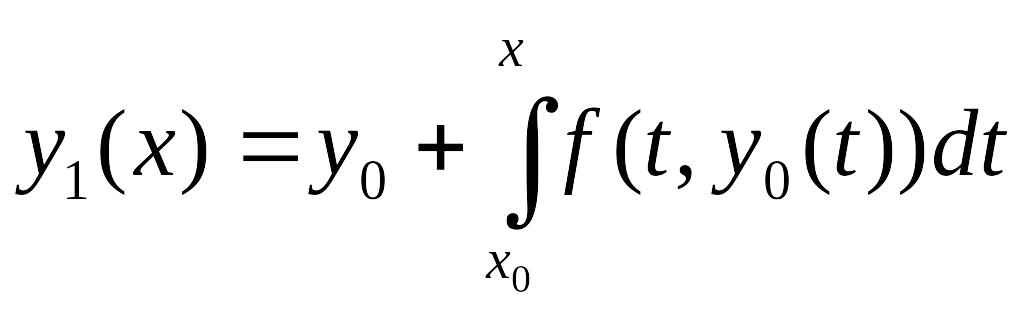
Его подстановка в (14.4) при п = 1 дает второе приближение

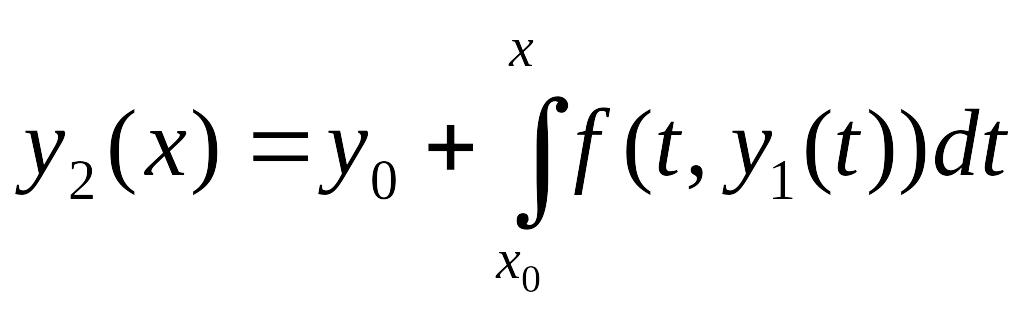
и т.д. Таким образом, этот приближенно-аналитический метод, называемый методом последовательных приближений или методом Пикара, определяется формулой

14.5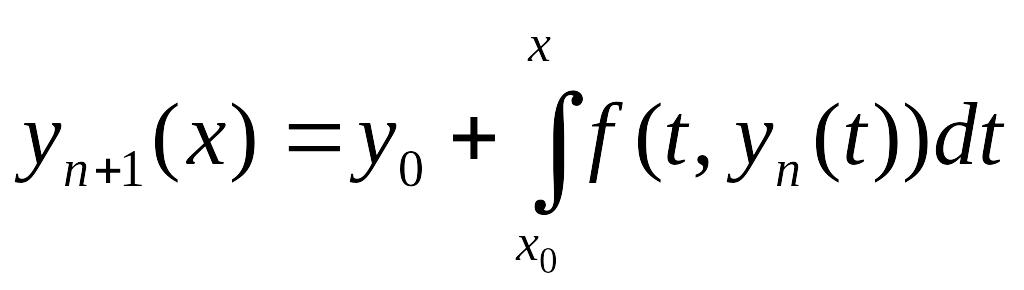

(14.5)

где п = 0,1, 2,... и у_о(х) = у₀.

Хорошо изучена сходимость метода (14.5). В частности, не вдаваясь в подробности, констатируем один качественный результат [62]:

если в некоторой односвязной области G, содержащей точку (х_о;у_о),

то найдется такая постоянная h>0, что на отрезке [x₀, x₀+H] последовательность функций у_п(х), определяемая методом (14.5), равномерно сходится к решению у(х) задачи Коши (14.1)—(14.2) и справедлива оценка погрешности

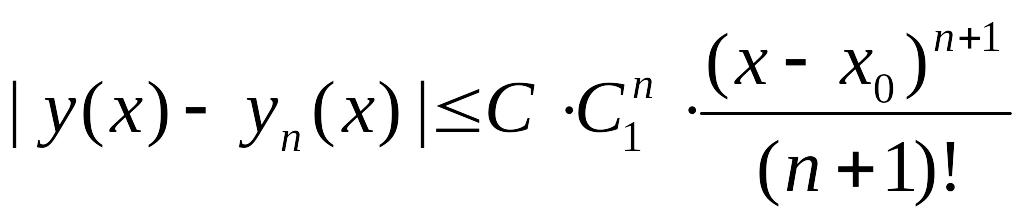
Отметим две характеристики метода последовательных приближений Пикара, которые можно отнести к негативным. Во-первых, в силу известных проблем с эффективным нахождением первообразных, в чистом виде метод (14.5) редко реализуем. Во-вторых, как видно из вышеприведенного утверждения, этот метод следует считать локальным, пригодным для приближения решения в малой правой окрестности начальной точки. Большее значение метод Пикара имеет для доказательства существования и единственности решения задачи Коши, нежели для его практического нахождения.

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.12.2018121.86 Кб1Материал для подготовки word.doc
#
18.09.2019117.25 Кб1Материал для подготовки word.doc
#
04.08.2019433.39 Кб1Материал_по_КП.docx
#
25.08.201962.05 Кб0Материалы и тесты по истории.docx
#
10.07.201992.34 Кб12Материалы по психологии менеджмента.docx
#
20.09.20193.52 Mб11матмод.doc
#
20.12.2018367.62 Кб2МАТСТАТ ВОПРОСЫ.doc
#
26.04.20191.4 Mб34мегашпора.doc
#
05.08.201965.54 Кб0медиаплан.doc
#
23.11.2019149.59 Кб3Международный менеджмент.docx
#
24.12.2018159.74 Кб3Мен.ответы.doc

X1	X2	X3	Y1	Y2
14	14	669	0	697
4	1	386	-3	391
7	25	675	18	707
2	1	642	-1	645
2	33	690	31	725
0	74	49	74	123
7	56	657	49	720
2	96	647	94	745
4	70	694	66	768
7	81	391	74	479
8	27	901	19	936

X1	X2	X3	Y1	Y2
14	14	669	0	697
4	1	386	-3	391
7	25	675	18	707
2	1	642	-1	645
2	33	690	31	725
0	74	49	74	123
7	56	657	49	720
2	96	647	94	745
4	70	694	66	768
7	81	391	74	479
8	27	901	19	936

X1	X2	X3	Y1	Y2
14	14	669	0	697
4	1	386	-3	391
7	25	675	18	707
2	1	642	-1	645
2	33	690	31	725
0	74	49	74	123
7	56	657	49	720
2	96	647	94	745
4	70	694	66	768
7	81	391	74	479
8	27	901	19	936