Ц.П.Т. Ляпунова

Пусть выполнены базовые предположения Ц.П.Т. Линдеберга. Пусть случайные величины имеют конечный третий момент. Тогда определена последовательность Если предел (условие Ляпунова), то

по распределению при .

38) Закон больших чисел.

Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.

Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.

Слабый закон больших чисел

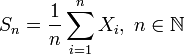
Тогда, .

Усиленный закон больших чисел

Тогда, .

Неравенство Чебышева

p( | X – M(X)| < ε ) ≥ D(X) / ε².

Доказательство. Пусть Х задается рядом распределения

Х	х1	х2	…	хп
р	р1	р2	…	рп

Так как события |X – M(X)| < ε и |X – M(X)| ≥ ε противоположны, то р ( |X – M(X)| < ε ) + + р ( |X – M(X)| ≥ ε ) = 1, следовательно, р ( |X – M(X)| < ε ) = 1 - р ( |X – M(X)| ≥ ε ). Найдем р ( |X – M(X)| ≥ ε ).

D(X) = (x1 – M(X))²p1 + (x2 – M(X))²p2 + … + (xn – M(X))²pn . Исключим из этой суммы те слагаемые, для которых |X – M(X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые kслагаемых. Тогда

D(X) ≥ (xk+1 – M(X))²pk+1 + (xk+2 – M(X))²pk+2 + … + (xn – M(X))²pn ≥ ε² (pk+1 + pk+2 + … + pn).

Отметим, что pk+1 + pk+2 + … + pn есть вероятность того, что |X – M(X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ≥ ε² р(|X – M(X)| ≥ ε), или р (|X – M(X)| ≥ ε) ≤ D(X) / ε². Тогда вероятность противоположного события p( | X – M(X)| < ε ) ≥ D(X) / ε², что и требовалось доказать

Теорема Чебышева:

Значение теоремы Чебышева для практики.

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемое сотнями.

В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико.

Уже из приведенных примеров можно заключить, что для практики теорема Чебышева имеет неоценимое значение.

39) Выборочный метод - статистический метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов, взятых на выборку.

Математи́ческая стати́стика — наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.

Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала (напр., оценить необходимый объём выборки для получения результатов требуемой точности при выборочном обследовании).

40) Основные параметры генеральной и выборочной совокупностей

. Повторная и бесповторная выборки

При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:

При бесповторном отборе она рассчитывается по формуле:

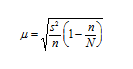
При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:

При бесповторном способе отбора средняя ошибка выборочной доли определяется по формуле:

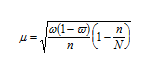
Репрезентати́вность — соответствие характеристик выборки характеристикам популяции или генеральной совокупности в целом. Репрезентативность определяет, насколько возможно обобщать результаты исследования с привлечением определённой выборки на всю генеральную совокупность, из которой она была собрана.

Также, репрезентативность можно определить как свойство выборочной совокупности представлять параметры генеральной совокупности, значимые с точки зрения задач исследования.