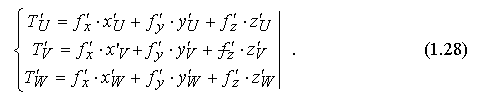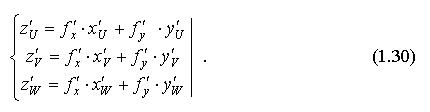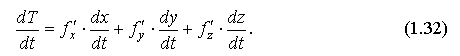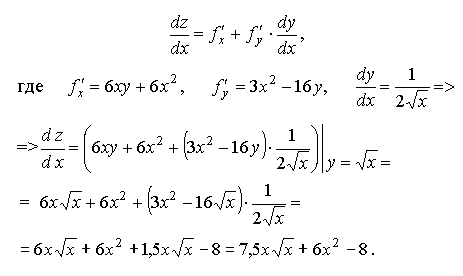19. Частные производные сложных функций. Полная производная.
Частные производные сложных функций нескольких переменных
Очень часто при решении практических задач (например, в высшей геодезии или аналитической фотограмметрии) появляются сложные функции нескольких переменных, т. е. аргументы x, y, z одной функции f (x,y,z)) сами являются функциями от новых переменных U, V, W). Так, например, бывает при переходе от неподвижной системы координат Oxyz в подвижную систему O0UVW и обратно. При этом важно знать все частные производные по "неподвижным" - "старым" и "подвижным" - "новым" переменным, так как эти частные производные обычно характеризуют положение объекта в этих системах координат, и, в частности, влияют на соответствие аэрофотоснимков реальному объекту. В таких случаях применяются следующие формулы:
То есть задана сложная функцияT трех "новых" переменных U, V, W посредством трёх "старых" переменных x, y, z, тогда:
Замечание. Возможны вариации в количестве переменных. Например: если
то
В частности, еслиz = f(xy), y = y(x) , то получаем так называемую формулу "полной производной":
Эта же формула "полной производной" в случае:
примет вид:
Возможны и иные вариации формул (1.27) - (1.32). Замечание: формула "полной производной" используется в курсе физики, раздел "Гидродинамика" при выводе основополагающей системы уравнений движения жидкости. Пример 1.10. Дано:
Найти
Решение Согласно (1.31):
Ответ:
|
Полная производная функции
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Полная
производная функции —
производная функции по времени вдоль
траектории. Пусть функция имеет вид
![]() и
ее аргументы зависят от времени:
и
ее аргументы зависят от времени:
![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]() —
параметры задающие траекторию. Полная
производная функции
—
параметры задающие траекторию. Полная
производная функции
![]() (в
точке
(в
точке
![]() )
в таком случае равна частной производной
)
в таком случае равна частной производной
![]() по
времени (в соответствующей точке
по
времени (в соответствующей точке
![]() )
и может быть вычислена по формуле:
)
и может быть вычислена по формуле:
![]() ,
,
где
![]() —
частные
производные.
Следует отметить, что обозначение
—
частные
производные.
Следует отметить, что обозначение
![]() является
условным и не имеет отношения к делению
дифференциалов.
Кроме того, полная производная функции
зависит не только от самой функции, но
и от траектории.
является
условным и не имеет отношения к делению
дифференциалов.
Кроме того, полная производная функции
зависит не только от самой функции, но
и от траектории.
Например,
полная производная функции
![]() :
:
![]()
Здесь
нет
![]() так
как
сама
по себе («явно») не зависит от
так
как
сама
по себе («явно») не зависит от
![]() .
.
20. Производные от функций заданных неявно.
Производная функции, заданной неявно
Уравнение
вида
![]() ,
содержащее переменные
,
содержащее переменные
![]() и
и
![]() ,
иногда можно разрешить относительно
и
получить в явном виде зависимость
,
иногда можно разрешить относительно
и
получить в явном виде зависимость
![]() .
Например, если дано уравнение
.
Например, если дано уравнение
![]() ,
то из него можно получить зависимость
,
то из него можно получить зависимость
![]() .
Однако такое явное выражение
через
,
использующее лишь элементарные функции,
можно получить не из любого уравнения
вида
(даже
если в самом уравнении участвуют лишь
элементарные функции). Например, хотя
уравнение
.
Однако такое явное выражение
через
,
использующее лишь элементарные функции,
можно получить не из любого уравнения
вида
(даже
если в самом уравнении участвуют лишь
элементарные функции). Например, хотя
уравнение
![]()
задаёт некоторую
зависимость
от
,
но выразить её из уравнения "в явном
виде" не удаётся. Тем не менее, некоторую
информацию об этой зависимости мы можем
получить, и не выражая
через
.
Например, в случае приведённого выше
уравнения, поскольку значения
![]() ,
,
![]() ему
удовлетворяют, мы можем утверждать, что
график этой зависимости проходит через
точку
ему
удовлетворяют, мы можем утверждать, что
график этой зависимости проходит через
точку
![]() плоскости
плоскости
![]() .
.
Покажем,
как, используя уравнение
,
найти производную
![]() ,
не выражая
через
в
явном виде. Для этого найдём производные
левой и правой части уравнения по
переменной
,
считая
промежуточным
аргументом, а потом выразим
,
не выражая
через
в
явном виде. Для этого найдём производные
левой и правой части уравнения по
переменной
,
считая
промежуточным
аргументом, а потом выразим
![]() из
получающегося равенства.
из
получающегося равенства.
Поясним сказанное на примере.
Пример
4.24 Возьмём то же
уравнение
![]() и
найдём производную левой части
(производная правой части, очевидно,
равна 0). Имеем:
и
найдём производную левой части
(производная правой части, очевидно,
равна 0). Имеем:
![]()
Слагаемые, содержащие , оставим в левой части, а остальные перенесём направо:
![]()
откуда
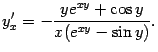
Получили выражение
для производной
,
содержащее, правда, не только
,
но и
в
правой части. Однако, несмотря на это,
полученное выражение можно использовать
для решения различных задач, связанных
с производной. Например, можно решить
такую задачу: найти для кривой, заданной
уравнением
,
уравнения касательной и нормали,
проведённых в точке
.
Действительно, при
![]() мы
получаем
мы
получаем
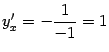 ,
так что нам теперь известен угловой
коэффициент касательной:
,
так что нам теперь известен угловой
коэффициент касательной:
![]() .
Точка касания дана условием задачи.
Поэтому уравнение касательной таково:
.
Точка касания дана условием задачи.
Поэтому уравнение касательной таково:
![]() или
или
![]()
а уравнение нормали -- таково:
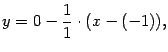 или
или
![]()
21. Частные производные высших порядков
Пусть
задана функция f(x, y). Тогда каждая
из ее частных
производных(если они, конечно,
существуют)
![]() и
и
![]() ,
которые называются также частными
производными первого порядка, снова
являются функцией независимых переменных
x, y и может, следовательно также
иметь частные производные. Частная
производная
,
которые называются также частными
производными первого порядка, снова
являются функцией независимых переменных
x, y и может, следовательно также
иметь частные производные. Частная
производная
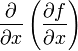 обозначается
через
обозначается
через
![]() или
или
![]() ,
а
,
а
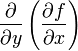 через
через
![]() или
или
![]() .
Таким образом,
.
Таким образом,
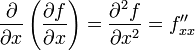 ,
,
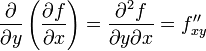
и, аналогично,
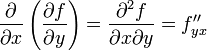 ,
,
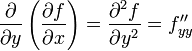 .
.
Производные
![]() и
и
![]() называются
частными производными второго порядка.
Определение:Частной производной
второго порядка от функции z=f(x;y)
дифференцируемой в области D,называется
первая производная от соответствующей
частной производной. Рассматривая
частные производные от них, получим
всевозможные частные производные
третьего порядка:
называются
частными производными второго порядка.
Определение:Частной производной
второго порядка от функции z=f(x;y)
дифференцируемой в области D,называется
первая производная от соответствующей
частной производной. Рассматривая
частные производные от них, получим
всевозможные частные производные
третьего порядка:
![]() ,
,
![]() ,
,
![]() и т. д.
и т. д.
22. экстремумы функций двух переменных, необходимые и достаточные условия.
Определение
1.11 Пусть задана функция двух переменных
z=z(x,y),
(x,y)![]() D.
Точка M0(x0;y0)
- внутренняя точка области D.
D.
Точка M0(x0;y0)
- внутренняя точка области D.
Если в D присутствует такая окрестность UM0 точки M0, что для всех точек
![]()
то точка M0 называется точкой локального максимума. А само значение z(M0) - локальным максимумом.
А если же для всех точек
![]()
то точка M0 называется точкой локального минимума функции z(x,y). А само значение z(M0) - локальным минимумом.
Локальный максимум и локальный минимум называются локальными экстремумами функции z(x,y). На рис. 1.4 поясняется геометрический смысл локального максимума: M0 - точка максимума, так как на поверхности z =z (x,y) соответствующая ей точка C0 находится выше любой соседней точки C (в этом локальность максимума).
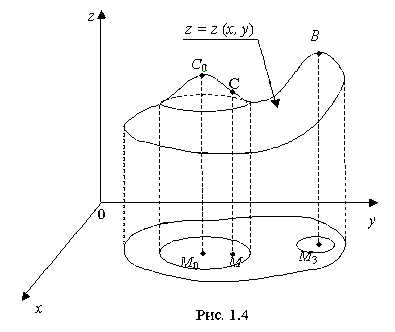
Заметим, что на поверхности в целом есть точки (например, В), которые находятся выше C0, но эти точки (например, В) не являются "соседними" с точкой C0.
В частности, точке В соответствует понятие глобального максимума:
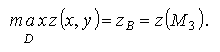
Аналогично определяется и глобальный минимум:
![]()
Нахождение глобальных максимумов и минимумов будет рассмотрено в п.1.10.
Теорема 1.3 (необходимые условия экстремума).
Пусть задана функция z =z (x,y), (x,y) D. Точка M0(x0;y0 D - точка локального экстремума.
Если в этой точке существуют z'x и z'y, то

Геометрическое доказательство "очевидно". Если в точке C0 на (рис.1.4) провести касательную плоскость, то она "естественно" пройдет горизонтально, т. е. под углом 0° к оси Ох и к оси Оу.
Тогда в соответствии с геометрическим смыслом частных производных (рис.1.3):
![]()
что и требовалось доказать.
Определение 1.12.
Если в точке M0 выполняются условия (1.41), то она называется стационарной точкой функции z (x,y).
Теорема 1.4 (достаточные условия экстремума).
Пусть задана z =z (x,y), (x,y) D, которая имеет частные производные второго порядка в некоторой окрестности точки M0(x0,y0) D. Причем M0 - стационарная точка (т. е. необходимые условия (1.41) выполнены). Вычислим:
![]()
Если:

Доказательство теоремы использует темы (формула Тейлора функции нескольких переменных и теория квадратичных форм), которые в этом пособии не рассматриваются.
Пример 1.13.
Исследовать на экстремум:
![]()
Решение
1. Найдём стационарные точки, решая систему (1.41):

то есть найдены четыре стационарные точки. 2.
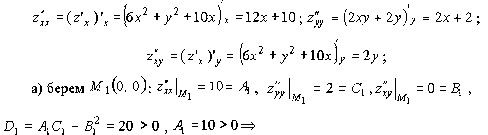
по
теореме 1.4 в точке
![]() –
минимум.
Причём
–
минимум.
Причём
![]()
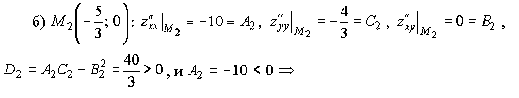
по теореме 1.4 в точке
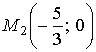
- максимум. Причём
![]()

23. определение двойного интеграла его геометрический смысл
Двойной интеграл - это обобщение определенного интеграла на двумерный случай. Т.е. для определения понятия двойного интеграла используется функция, зависящая уже от двух переменных: f(x,y). Эта функция должна быть определена на некоторой, обладающей конечной площадью, области D плоскости X0Y. При этом граница области D должна состоять из конечного числа графиков непрерывных функций. Не трогать